Определим дебит горизонтальной скважины, длиной L , расположенную в пласте толщиной h, контур питания скважины примем - радиус Rк, давление на контуре питания - Pк, с абсолютной проницаемостью - K, динамическая вязкость дренируемой жидкости - m, , давление на забое скважины - Pс, приведенный радиус скважины - rс. Предположим, что данная скважина расположена симметрично относительно кровли и подошвы пласта (рис. 1).

Рис. 1- Схема расположения симметричного ствола горизонтальной скважины по толщине пласта.
Над решением данной задачи работали Ю.Т.Борисов и В.П.Табаков [1-5]. Согласно их исследованиям дебит горизонтальной скважины выражается формулой:
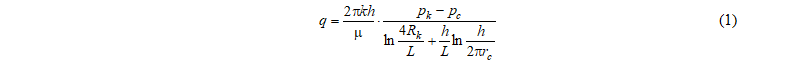
Если мы рассмотрим с физической точки зрения знаменатель, то первое слагаемое в отражает внешнее фильтрационное сопротивление, второе - внутреннее сопротивление скважины.
Данная формула строится на основании предположения, что контур питания горизонтальной скважины предполагается радиальным, и не зависит от длины горизонтальной скважины.
С учетом того, что Giger F [6] выдвинул предположение, согласно которому контур питания горизонтальной скважины носит эллипсообразный, а не круговой характер, он представил свою формулу для расчета горизонтальной скважины:
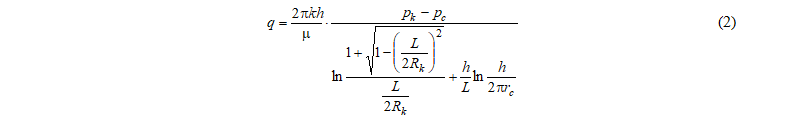
здесь Rк – контур питания, представляющий большую полуось эллипса.
oshi S. [7] предположил, что есть большая полуось эллипса, аналогичного по площади кругу с радиусом дренирования Rк, подставив которую в формулу (1.2) он получил выражение:
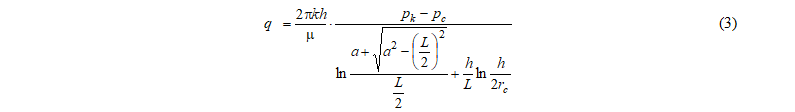
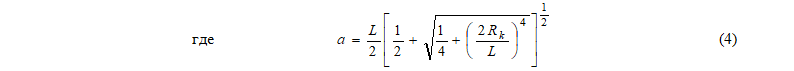
есть большая полуось эллипса.
В работе Renard G., Dupuy J. [8] была предложена формула, для расчета дебита горизонтальной скважины:
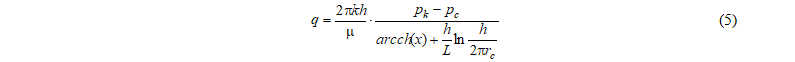
где x = 2a / L и a вычисляются по формуле (1.4).
Вышеуказанные формулы применимы для изотропных пластов, которые практически не встречаются в процессе разработки месторождений! Для анизотропных пластов предложены другие формулы:
Renard, Dupuy [8] предложил следующую формулу для анизотропного пласта
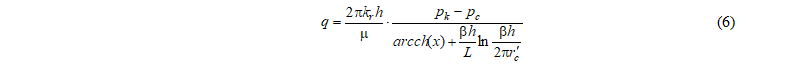

Joshi [7] предложена формула определения дебита горизонтальной скважины, учитывающая анизотропию пласта по проницаемости:
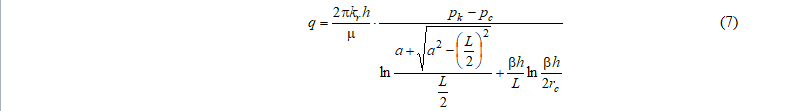
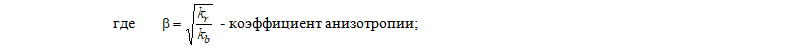
кг - проницаемость пласта в горизонтально направлении;
кв - проницаемость по вертикали.
Однако, формулы 2 – 6 можно применять и в случае анизотропных пластов, если выполняются следующие условия: Длина скважины много больше толщины пласта, половина длины горизонтальной скважины меньше чем 90% от радиуса контура питания и длина скважины больше произведения коэффициента анизотропии на толщину пласта (L > b × h)
И.А. Чарный [9] предложил следующую формулу для условия, когда горизонтальный ствол скважины расположен симметрично контуру питания:
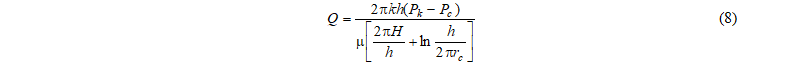
где k - проницаемость пласта; Pк, Pс - давления на контуре питания и на забое скважины; μ - вязкость нефти; Н – расстояние от скважины до границы пласта; h – толщина пласта; rc - радиус скважины.
Произведем расчет прогнозного дебита нефти для горизонтальных скважин Авиловского месторождения волгоградской области. Авиловское месторождение расположено на территории Котовского района Волгоградской области на Авиловской площади. В 2007 году с целью изучения сводовой залежи была пробурена поисковая скважина 6 Авиловская, которая стала первооткрывательницей Авиловского газонефтяного месторождения. Продуктивными отложения расположены на уровне бобриковского горизонта. Введено в пробную эксплуатацию в 2013 году. На данном месторождении пробурено 8 скважин из них: Авиловская-1 – ликвидирована; Авиловские-8 и -112 – остановлены по причине достижения предельной обводненности; Авиловские-6, -111, -114, -7, -113– добывающие. По состоянию на 01.12.2016 г. Залежь нефти водоплавающая, с газовой шапкой.
Исходные данные по скважинам представлены в таблице ниже в таблице 1, коэффициенты эллипса дренирования выбирались следующим образом: а – эффективная нефтенасыщенная толщина для горизонтальной скважины, а b – средняя толщина пласта. – проницаемость керна по нефти, Рк-давление на расстоянии R от оси скважины, Рс- забойное давление, - приведенный радиус скважины, k- проницаемость пласта. -динамическая вязкость, а и в – радиусы эллипса дренирования.
Таблица 1
|
исходные данные
|
Номера скважин |
|||||
|
7 |
111 |
114 |
113 |
8 |
112 |
|
|
в пл. усл, мПа*с |
0,47 |
0,48 |
0,46 |
0,47 |
0,44 |
0,46 |
|
Рк,МПа |
20,73 |
20,72 |
20,51 |
20,90 |
20,70 |
20,90 |
|
Pс ,МПа (забойное давление) |
20,27 |
20,04 |
19,91 |
20,00 |
20,38 |
19,60 |
|
Rк , м |
298,37 |
371,68 |
442,56 |
496,17 |
217,31 |
1605,51 |
|
kабсолют мД |
125,70 |
178,20 |
0,30 |
158,00 |
83,00 |
12,60 |
|
Гс, см |
7,15 |
7,15 |
7,15 |
7,15 |
7,15 |
7,15 |
|
L, длина скважины , м |
123,00 |
257,00 |
287,00 |
466,00 |
302,00 |
293,00 |
Примем начальное пластовое давление= давлению на контуре питания. С учетом того, что коллектор представляет собой песчаник, примем допущение, что свойства пласта изотропны. Ввиду одновременной фильтрации нескольких фаз для расчета используем величину относительной фазовой проницаемости по нефти, которая значительно меньше, чем абсолютная проницаемость.
Радиус контура питания скважины рассчитаем при помощи формулы выведенной в статье А.В. Казанцева [10]:
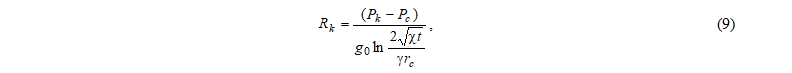
где χ – коэффициент пьезопроводности пласта 970 см2/с, γ=1,781072418 постоянная Эйлера, rc - радиус скважины по долоту = 14,29 см, g0 – пороговый градиент давления = 0,00063 МПа/м [11],
Расчеты дебита скважины произведем согласно вышеуказанным формулам, а так же проанализируем точность расчета дебита скважины по данным формулам с фактическим дебитом.
Таблица 2
|
исходные данные
|
Номера скважин |
|||||
|
7 |
111 |
114 |
113 |
8 |
112 |
|
|
χ – коэффициент пьезопроводности пласта см2/с |
5300 |
13500 |
3000 |
12845 |
4100 |
530 |
|
Rк, м |
298,37 |
371,68 |
442,56 |
496,17 |
217,31 |
1605,51 |
|
Фактический дебит скважины, м3/сут |
68 |
78 |
90 |
40 |
77 |
90 |
|
По формуле Ю.Т.Борисова и В.П.Табакова , м3/сут |
269.2 |
740.9 |
1.1 |
1098.8 |
284.2 |
61.6 |
|
По формуле Giger F, м3/сут |
270.4 |
753.7 |
1.1 |
1144.9 |
328.0 |
61.7 |
|
По формуле Joshi S., м3/сут |
259.5 |
723.3 |
1.1 |
1080.0 |
273.3 |
60.9 |
|
По формуле Renard G., Dupuy J., м3/сут |
Значения не получены |
Значения не получены |
Значения не получены |
Значения не получены |
Значения не получены |
Значения не получены |
|
По формуле И.А. Чарного, м3/сут |
1442.1 |
2972.1 |
4.6 |
3577.1 |
700.2 |
423.8 |
Выводы:
Произведенные расчеты обнаружили, что использование данных формул неприемлемо для расчета дебита Авиловского месторождения.
Однако можно отметить некоторую схожесть расчетов, при применении фрмул Ю.Т.Борисова и В.П.Табакова, Giger F, Joshi S., отсюда можно сделать вывод, что данные формулы применимы для фильтрации происходящей по линейным законам, а так же для законам при определенных условиях.
Так же можно отметить, что расчет дебита горизонтальной скважины по формуле Renard G., Dupuy J. Затруднено, ввиду существенных ограничений применимости данной формулы.
Все исходные данные были проверены и имеются заключения о том, что данные, взятые для расчетов корректны.
Большая погрешность в расчетах обусловлена наличием высокого газового фактора, на скважинах Авиловского месторождения, газовый фактор изменялся в пределах от 200 до 15 000 м3/т. Соответсвенно, говорить о линейной фильтрации в условиях данного газонефтяного месторождения не представляется возможным. Для определения дебита горизонтальной скважины, в условиях высокого газового фактора необходимо использовать иные формулы для расчета. И произведенные расчеты по классическим формулам наглядно подтверждают это.
Литература:
1. Борисов Ю.П., Пилатовский В.П., Табаков В.П. Разработка нефтяных месторождений горизонтальными и многозабойными скважинами. М.: Изд. Недра, 1964.
2. Борисов Ю.П., Табаков В.П. Определение дебита многоярусной скважины в изотропном пласте большой мощности. НТС по добычи нефти ВНИИ. Выпуск 16. М.: Гостоптехиздат, 1962.
3. Табаков В.П. О притоке нефти к многозабойным скважинам в плоском пласте. НТС по добыче нефти ВНИИ. Выпуск 13, М.: Гостоптехиздат, 1960.
4. Табаков В.П. Определение дебита и эффективности многозабойной скважины в слоистом пласте. НТС по добыче нефти ВНИИ. Выпуск 10, М.: Гостоптехиздат, 1960.
5. Табаков В.П. Приток жидкости к батарее наклонных скважин в слоистом пласте. НТС по добыче нефти ВНИИ. Выпуск 10, М.: Гостоптехиздат, 1960.
6. Giger F.M. The Reservoir Engineering Aspects of Horizontal Drilling. SPE 13024, 1984.
7. Joshi S.D. Horizontal well technology. Oklahoma. 1991.
8. Renard G.I., Dupug J.M. Influence of Formation Damage on the flow Efficiency of Horizontal Wells. Paper SPE 19414, Louisiana 1990.
9. Чарный И.А. Подземная гидромеханика. Выпуск 3, М.: ОГИЗ. 1954.
10 А.В. Казанцев, Расчет радиуса контура питания нефтяных скважин, Исслед по информ., 2001, выпус 3, с. 145-148.
11. О.Н. Шевченко, Определение значений критических градиентов давления и скорости фильтрации неньютоновской жидкости, Международный научно-исследовательский журнал № 3(45) 2016 Часть 2 стр 120-125.
12. И.Н. Хакимзянов, Р.С. Хисамов, И.М. Бакиров, Вопросы оптимизации и повышения эффективности эксплуатации скважин с горизонтальным окончанием на основе математического моделирования месторождений Татарстана,Казань, 2014 г., 240 с.






