Многоканальные кинематические фильтры при обработке морских наблюдений

Подавление спутника – одна из классических задач обработки сигналов в сейсморазведке. Несмотря на то, что задача старая, на протяжении многих лет ей уделялось сравнительно мало внимания, возможно, из-за того, что заглубления кос и источников всегда были невелики, и в этих случаях задача относилась к деконволюционным. Спутник относился к форме сигнала, и его влияние в значительном диапазоне частот было сравнительно невелико. Ситуация изменилась, когда стали применять заглубленные косы и появились донные наблюдения. Заглубление косы приемников стало популярно из-за того, что при его использовании значительно ослабляется уровень шумов, связанных с волнением моря, и других помех, распространяющихся близко к поверхности. Это позволяет получать записи и на низких частотах, важность которых особенно велика при решении задач волновой динамической инверсии. Снова возникла проблема подавления спутника, причем в самой трудной постановке, когда коэффициент второго удара близок к единице, а время вступления второго сигнала измеряется десятками миллисекунд. В последнее время эта тема приобрела особую популярность. Речь шла преимущественно об особых системах наблюдений, таких, например, как GeoStreamer, когда измерения одновременно осуществляются геофонами и гидрофонами (Ампилов, 2015). В этом случае возникает другая проблема – приведение формы волны, зарегистрированной гидрофоном к форме волны, зарегистрированной геофоном. Этих вопросов мы здесь почти не касаемся. Кратко отметим возникающие здесь проблемы в заключительной части. В данной работе мы попробуем подытожить исследования, подробно освещенные в цикле статей (Рябинский М.А., Фиников Д.Б., 2016) и докладов (Рябинский М.А., Фиников Д.Б., 2015-2016), где обсуждались возможности решения задачи с разных точек зрения и при различных системах однокомпонентных наблюдений.

Подавление спутника в одномерном случае

Задача подавления спутника в одномерном случае формулируется довольно просто. На нем особенно удобно показывать как суть задачи, так и главные сложности ее решения. Модель описывается суммой трассы без спутника и ею же, подвинутой на задержку, которая зависит от известных параметров. При этом задача восстановления трассы без спутника оказывается некорректной, на некоторых частотах спектр трассы равен 0 и спектр трассы без спутника не восстанавливается. Такого рода сложности могут быть преодолены только нелинейными преобразованиями, одно из которых и было предложено в работе (Гофман П., Фиников, 2014) и развито в работе (Рябинский М, Фиников, 2016). Рассчитываются два решения: одно «стандартное» – подавление спутника с регуляризацией, а другое получают в обращенном времени. Получают полезный сигнал из спутника. Из этих решений делают выпуклую комбинацию (суммируют с положительными весами, сумма которых равна 1), подбирая ее по критерию минимума энергии. В этом случае критерий минимума энергии оправдан, т.к. задача решается с ограничением на положительность весов. Этот прием обобщается и на многомерный случай, к рассмотрению которого переходим.

Многоканальная кинематическая фильтрация

Кинематическая фильтрация – это многоканальная фильтрация, предложенная В.М. Глоговским и Д.Б. Финиковым в 80-е годы для решения задач преобразования волновых полей, полностью определяемых кинематикой полезных волн и помех (Глоговский, Фиников, 1987). Критерий кинематической фильтрации для подавления волн-спутников при 2D наблюдениях можно сформулировать следующим образом:

Здесь – набор эталонных сигналов на локальной базе фильтра, в качестве которых в данном случае используются плоские волны, 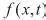– искомая импульсная характеристика кинематического фильтра, преобразующего зарегистрированное волновое поле со спутником в поле отраженных волн без спутника, – лучевые параметры отраженной волны и спутника соответственно при подходе к линии наблюдений, – диапазон лучевых параметров отраженной волны, – временная задержка спутника относительно отраженной волны, 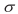– коэффициент учета спутника, соответствующий коэффициенту отражения от дневной поверхности. Если множитель поставить в выражении перед первым слагаемым (сигналом), то получится фильтр, развернутый в обратном времени, т.е. трансформирующий спутник в сигнал и подавляющий исходный сигнал как спутник, аналогично одномерному случаю. Критерий очевидным образом можно обобщить на случай 3D наблюдений, заменив лучевые параметры и , а также координату , соответствующими двумерными векторами.

Пусть дневная поверхность горизонтальна, а линия приемников располагается параллельно ей на глубине . В этом случае легко показать, что

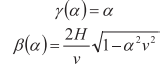
_{где v – скорость звука в воде.}

Из последнего выражения следует, что с ростом угла подхода задержка спутника относительно отраженной волны 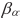уменьшается, а когда фронт отраженной волны горизонтален, достигает своего максимума, равного .

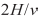Приведем модельный пример работы процедуры подавления спутника.

РИС. 1. Изображение операторов кинематического фильтра: а – в прямом времени



РИС. 1. Изображение операторов кинематического фильтра: б – в обратном времени

На рис. 1а показан 41-канальный оператор подавления спутника, на рис. 1б – оператор, трансформирующий спутник в сигнал и подавляющий исходный сигнал как спутник. Операторы посчитаны для горизонтальной косы, заглубленной на 40 метров, коэффициент учета спутника задан равным .

РИС. 2. Результат фильтрации в прямом и обратном времени: а – модельная сейсмограмма со спутником



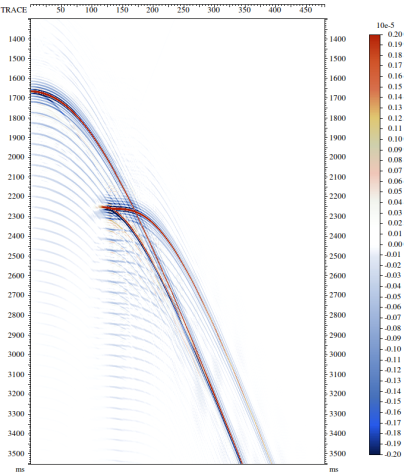
РИС. 2. Результат фильтрации в прямом и обратном времени: б – результат фильтрации в прямом времени



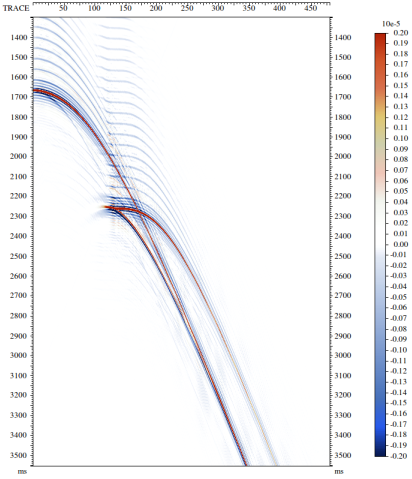
РИС. 2. Результат фильтрации в прямом и обратном времени: в – результат фильтрации в обратном времени

На рис. 2 представлена модельная сейсмограмма ОПВ со спутником и результат применения к ней двух описанных операторов фильтра. В данном случае в результате фильтрации образуется затухающий «хвост», подобный тому, что был описан в случае одномерной рекурсивной фильтрации. Для борьбы с этим эффектом можно применить также описанную выше процедуру адаптивного суммирования двух результатов (в прямом и в обратном времени) с подбором весов по критерию минимума энергии. В итоге мы получаем изображение (см. рис. 3), на котором артефакты фильтрации практически не заметны. Алгоритм особенно важен тогда, когда запись содержит элементы, не описывающиеся моделью спутника (например, прямую волну или помеху не связанную с полем восходящих волн).

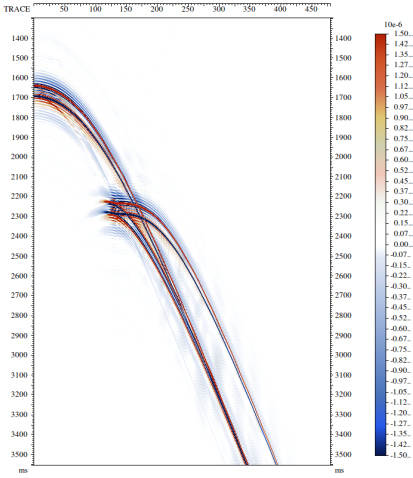
РИС. 3. Адаптивная сумма результатов кинематической фильтрации: а – модельная сейсмограмма со спутником



РИС. 3. Адаптивная сумма результатов кинематической фильтрации: б – адаптивная сумма результатов фильтрации

В работе (Рябинский М.А., Фиников Д.Б, Ч.2, 2016) рассмотрены два специальных метода наблюдений: с наклонной косой и двумя горизонтально заглубленными косами. Для того чтобы иметь возможность заниматься сопоставлением различных методов сбора сейсмических данных, прежде всего, нужно научиться корректным образом обрабатывать материалы, зарегистрированные при помощи каждого из таких методов. Способ кинематической фильтрации морских данных позволяет выполнять процедуру подавления спутника единообразно для любой однокомпонентной схемы наблюдений путем оптимизации единого критерия качества. Из анализа модельных примеров, приведенных в статье, можно сделать вывод о том, что наклонная коса не обладает сколь-нибудь существенными преимуществами по отношению к горизонтальной при корректной обработке. Система двух кос, погруженных на разные уровни, обеспечивает наилучший результат, что понятно и из общих соображений. Здесь могут возникать труднопреодолимые сложности инженерного и экономического характера при реализации однокомпонентных наблюдений.

Подавление спутника – существенно трехмерная задача

С самого начала мы декларировали, что способ кинематической фильтрации годится и для обработки трехмерных данных. Между тем трехмерность реального поля, когда волны могут приходить не из вертикальной плоскости, при подавлении спутника часто игнорируют. Артефакты фильтрации, обусловленные недоучетом размерности, могут быть очень существенны. Учесть размерность непросто, когда речь идет о реальной плотности наблюдений.

Для иллюстрации проблемы размерности мы рассчитали модельное волновое поле в существенно трехмерной среде. Модель изображена на рис.4, она состоит из двух отражающих границ (см. рис. 4а): горизонтальной свободной поверхности «вода-воздух» (изображена синим цветом) и вогнутой поверхности морского дна (изображена зеленым цветом). На рис. 4б представлена карта глубин по горизонту дна.

Далее в условиях рассмотренной глубинно-скоростной модели среды (скорость распространения волн в водном слое задана равной 1500 м/с) была рассчитана трехмерная сейсмограмма общего пункта возбуждения. Координаты пункта возбуждения (ПВ) соответствуют геометрическому центру модели (Х = 7500 м, Y = 2500 м), линии приема расположены справа от ПВ с шагом 12,5 м, шаг между каналами на одной линии приема также равен 12,5 м

РИС. 4. Модель существенно трехмерной среды: а – взаимное расположение отражающих границ среды



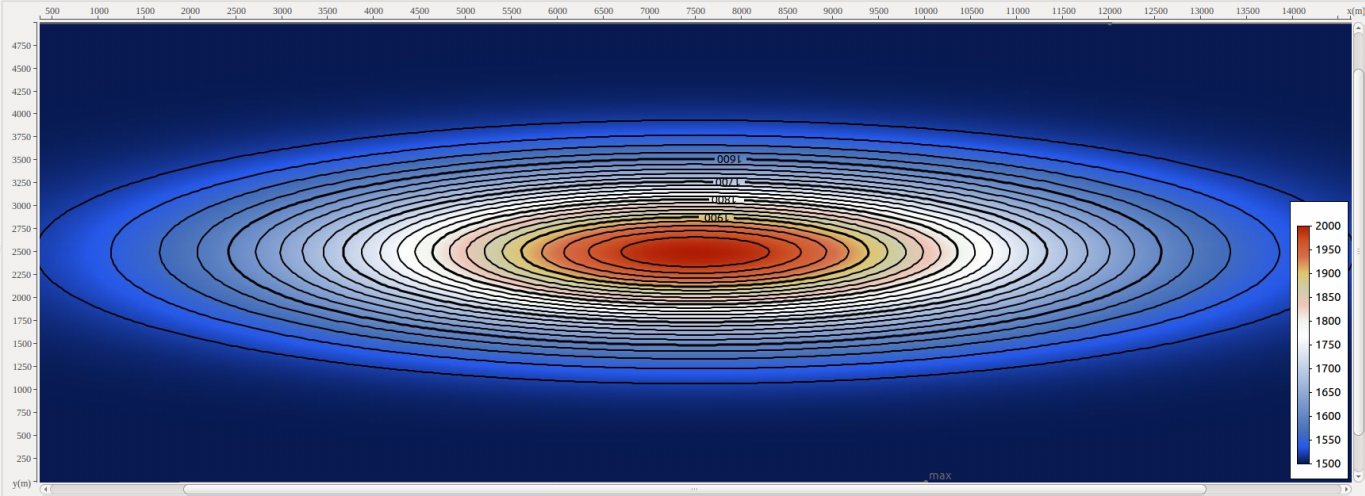
РИС. 4. Модель существенно трехмерной среды: б – карта глубин горизонта морского дна

Длина расстановки по ин-лайну составляет 6000 м, по кросс-лайну – 2000 м. При моделировании была использована горизонтально погруженная плоскость приема с заглублением 23 м.

На рис. 5 показан пример работы двумерного фильтра. Важно, что использовалась адаптивная схема сложения результатов подавления спутника в прямом и обращенном времени, иначе уровень помех преобразования был бы сильнее.

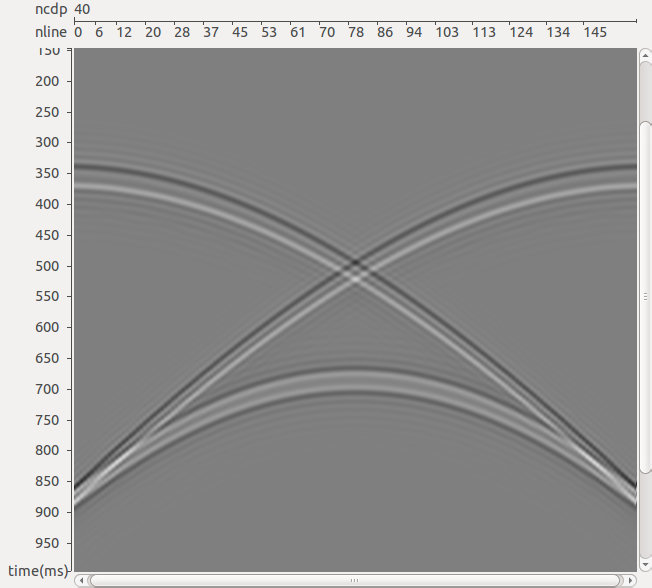
РИС. 5. Результат работы двумерного алгоритма подавления спутника: а – исходные данные



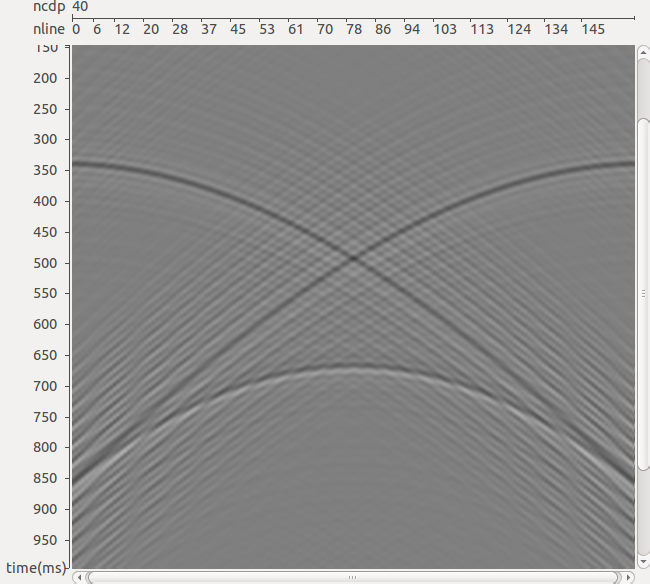
РИС. 5. Результат работы двумерного алгоритма подавления спутника: б – результат подавления спутника

На рис. 6 приводится результат работы трехмерного фильтра, который точно решает задачу с использованием обращенного предсказания спутника. Такого изображения удается добиться путем учета угла подхода отраженной волны в направлении вдоль как ин-лайна, так и кросс-лайна.

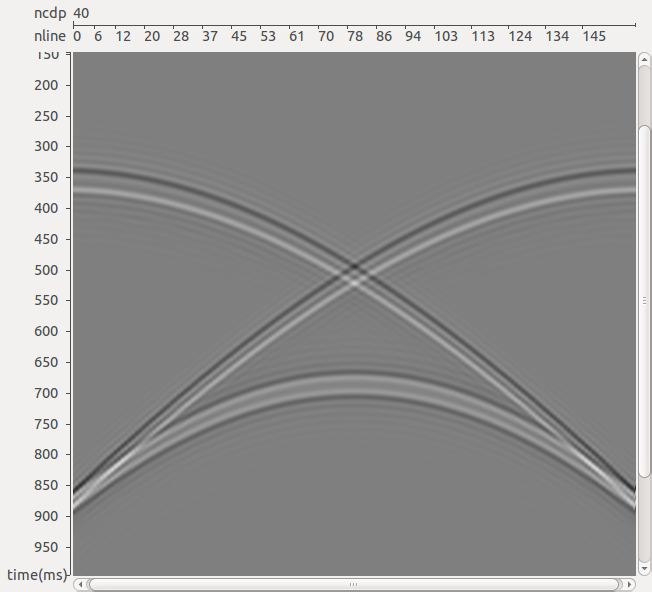
РИС. 6. Результат работы трехмерного алгоритма подавления спутника: а – исходные данные

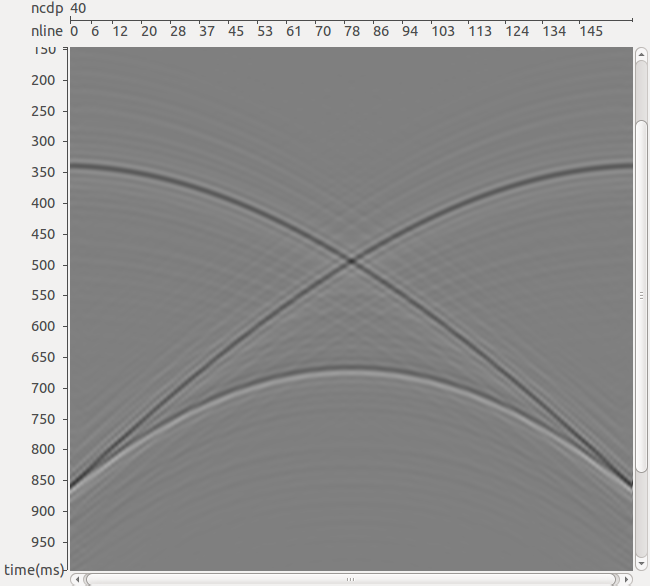
РИС. 6. Результат работы трехмерного алгоритма подавления спутника: б – результат подавления спутника

Итак, задача подавления спутника существенно трехмерна. Артефакты, вызванные неучетом размерности, могут проявляться не всюду, а именно в области отображения существенно трехмерных объектов.

Трехмерность среды надо учитывать и при пересчете волнового поля на дневную поверхность. Без этого вся дальнейшая обработка данных, полученных с заглубленными приемниками, будет содержать погрешности, неизменно приводящие к ошибкам в глубинных построениях. Это непростая задача при реальных дискретностях в наблюдениях волнового поля.

Показанный выше пример подавления спутника трехмерным фильтром демонстрирует принципиальную разрешимость задачи, но на практике применить такой фильтр вряд ли удастся, если данные не обладают столь подробной дискретностью по обеим координатам. Обычно в морской сейсморазведке такая дискретность не обеспечивается. Необходимо применять процедуры интерполяции волновых полей. Рассмотрим, какие возможности предоставляют кинематические фильтры для решения этой задачи. Акцент будет сделан на подавлении спутника, хотя проблема дискретности может обсуждаться в более широком контексте.

Интерполяция методом кинематической фильтрации

Проблема интерполяции волновых полей является одной из старейших в сейсморазведке. Здесь мы сосредоточимся только на технике, которую нам предоставляет развиваемый нами способ кинематической фильтрации. Алгоритм трехмерной регуляризации и интерполяции при помощи кинематической фильтрации кратко был описан в тезисах к докладу [Фиников, Рябинский, «EAGE Геомодель», 2016], он состоит из следующих этапов:

1. Расчет набора оптимальных кинематических фильтров, соответствующий заданному набору диапазонов наклонов. Каждый фильтр предназначен для регуляризации и интерполяции исходных данных в соответствующем диапазоне наклонов.

2. Применение каждого фильтра из рассчитанного набора к исходным редким данным. В результате будут получены наборы регулярных данных, отфильтрованные в заданных диапазонах наклонов.

3. Выбор трасс в каждом наборе, соответствующих (геометрически) исходным редким данным. Подбор коэффициентов проецирования выбранных данных на исходные трассы.

4. Интерполяция полученных коэффициентов на подробную геометрию.

5. Применение результирующего поля коэффициентов для комбинирования ответов п. 2 в окончательный результат интерполяции.

Таким образом, в результате выполнения п.1-2 алгоритма интерполяции из исходного набора (нерегулярных) данных получают несколько подробных наборов, каждый из которых отфильтрован в одном из заданных диапазонов наклонов . Каждая трасса исходного набора также подвергается аналогичной фильтрации, поэтому на третьем этапе алгоритма выполняется проецирование результатов этой фильтрации на исходные (нефильтрованные) трассы. Отметим, что этот этап выполняется в скользящем временном окне, что обеспечивает локальность процедуры по времени. Затем полученное редкое поле коэффициентов проекций распространяется на нужную подробную (по удалениям) сеть наблюдений.

Для иллюстрации работы алгоритма интерполяции применительно к задаче подавления спутника рассмотрим модель наблюдений, аналогичную описанной выше. Разница состоит лишь в выборе более реалистичного с точки зрения практики морских сейсмических исследований шага между линиями приема, а именно 100 м, вместо использовавшихся ранее 12,5 м. В этом случае перед применением трехмерного алгоритма подавления спутника используется описанный выше трехмерный алгоритм интерполяции данных вдоль кросс-лайнов. На рис. 7б представлен результат интерполяции сейсмограммы ОПВ на сечении вдоль кросс-лайна на удалении 500 м от ПВ по оси Х (том же, что рассматривался ранее). Использовались 40-канальные фильтры (размер базы равен 100 м вдоль ин-лайнов и 500 м вдоль кросс-лайнов), рассчитанные в каждом из 32 диапазонов наклонов (от 0 до 4 отсчетов за канал вдоль ин-лайнов и от -4 до 4 отсчетов за канал вдоль кросс-лайнов), размер временного окна задавался равным 70 мс. Рис. 8а иллюстрирует исходное сечение сейсмограммы ОПВ с шагом 100 м между каналами, а рис. 8в – модельную сейсмограмму, рассчитанную с шагом 12,5 м. Качественно результат интерполяции (см. рис. 7б) вполне сопоставим с «идеальной» моделью (см. рис. 7в), однако на нем наблюдаются слабые погрешности все в той же зоне «конфликтных» наклонов. Эти погрешности могут быть устранены путем усовершенствования метода интерполяции поля коэффициентов проекции, использующегося в п.4 описанного выше алгоритма. В данном случае применялась билинейная интерполяция, вместо нее могут быть использованы двумерные сплайны, кригинг и т. п. Тем не менее, как показано на рис. 8, даже полученного качества интерполяции оказывается вполне достаточно для выполнения трехмерного алгоритма подавления спутника. Даже в тех частях сейсмограммы, где интерполяция сработала «не очень чисто», многоканальная процедура подавления спутника сгладила погрешности интерполяции и позволила получить результат, качественно мало отличающийся от результата в «идеальной» модели.

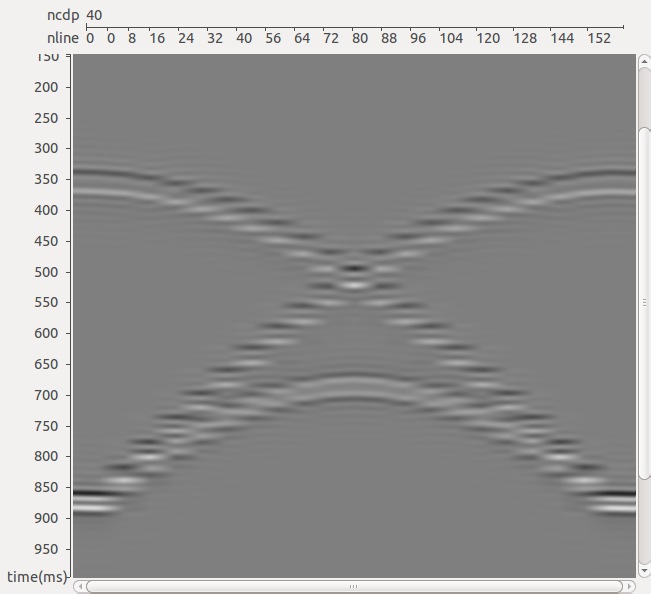
РИС. 7. Результат трехмерной интерполяции методом кинематической фильтрации: а – исходное сечение сейсмограммы ОПВ (100 м между каналами)



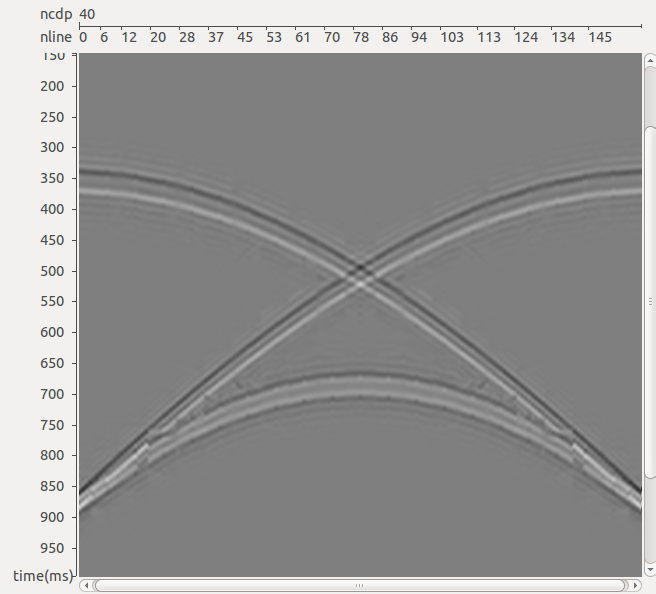
РИС. 7. Результат трехмерной интерполяции методом кинематической фильтрации: б – результат интерполяции (12,5 м между каналами)



РИС. 7. Результат трехмерной интерполяции методом кинематической фильтрации: в – «идеальная» модель (12,5 м между каналами)

С точки зрения практического использования описанного подхода для обработки реальных морских наблюдений важными его особенностями являются локальность (по пространственным координатам) и трехмерность. Возможность использовать операторы, рассчитанные на целые диапазоны наклонов, – важное технологическое преимущество подхода.

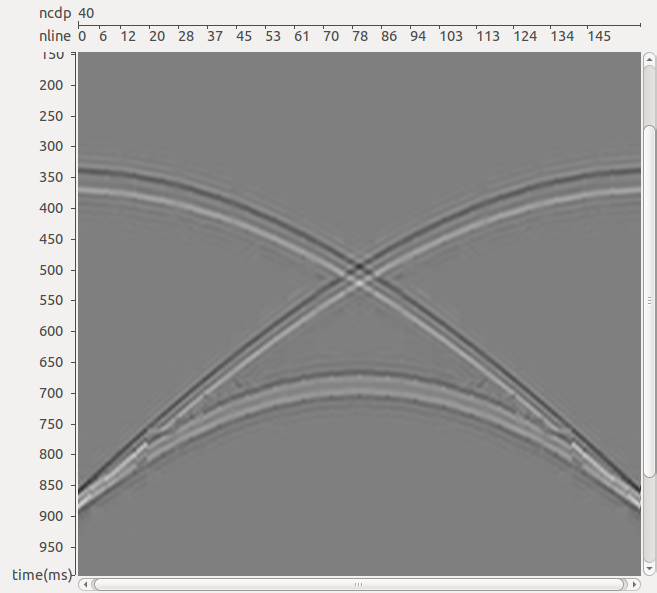
РИС. 8. Результат трехмерного подавления спутника после интерполяции данных: а – результат интерполяции



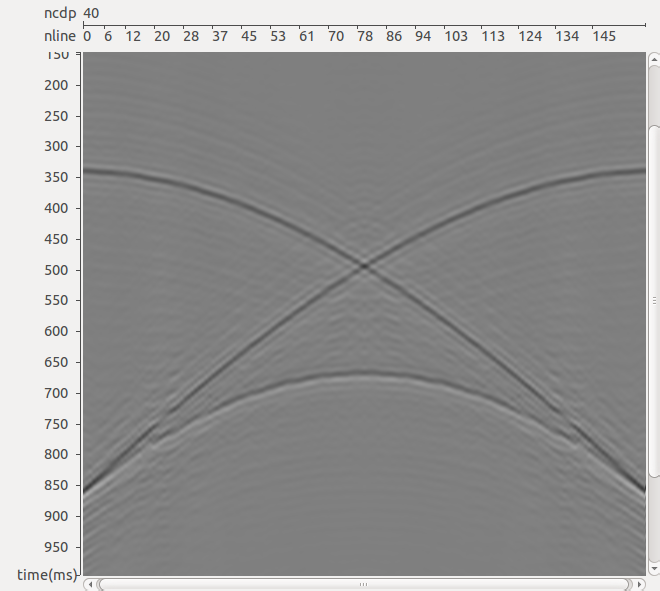
РИС. 8. Результат трехмерного подавления спутника после интерполяции данных: б – результат подавления спутника после интерполяции



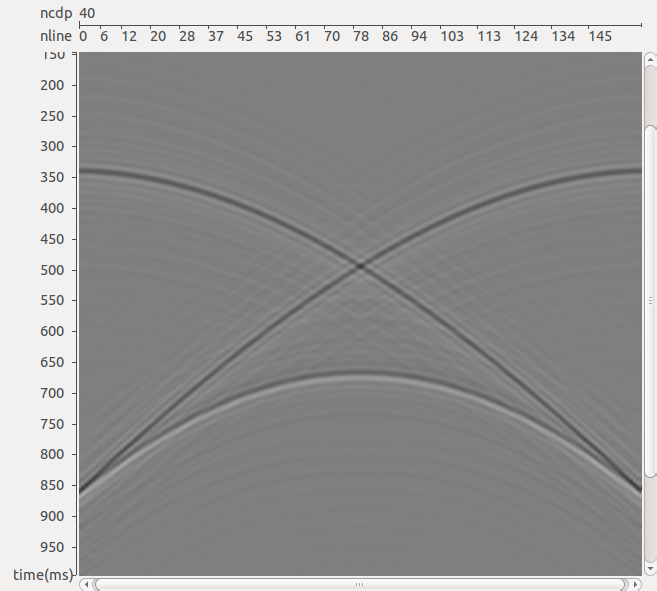
РИС. 8. Результат трехмерного подавления спутника после интерполяции данных: в – результат подавления спутника в «идеальной» модели

В дальнейшем мы рассчитываем и на возможность расширения базиса «эталонных сигналов» (включение в него не только линейных, но и параболических событий), развитие способов оптимизации при поиске коэффициентов разложения поля по набору фильтрованных компонент.

Конечно, техника интерполяции выходит далеко за рамки статьи, посвященной подавлению спутников. Однако важно было показать, что интерполяция должна (и может) обеспечить сохранение динамических особенностей записи, позволяющее решать и столь нетривиальные задачи обработки.

Заключение

В заключении хотелось бы отметить, что описанные алгоритмы интерполяции и подавления спутника позволяют работать в достаточно широком диапазоне частот, как того и требуют современные стандарты BroadBand. Мы рассматривали только способы обработки стандартных однокомпонентных наблюдений. Многокомпонентные наблюдения дают больше возможностей по разделению волн на падающие и восходящие, но следует иметь в виду, что проблемы дискретности остаются и в этом случае: они возникают при приведении по форме и амплитуде полезных сигналов данных геофонов к данным гидрофона. Если этот этап выполнен некорректно – подавление спутника может быть неэффективным. Однако несомненным преимуществом здесь является то, что процедуры разделения на падающие и восходящие волны не порождают дополнительных шумов и артефактов, даже когда могут и не справляться с поставленной задачей.

При обработке и интерпретации данных с заглубленными косами следует иметь в виду, что шумы и артефакты, обусловленные недоучетом тех или иных факторов, могут возникать локально. Так в верхней части, там, где годографы наблюденных волн более крутые, содержатся прямые волны (или их не до конца подавленные остатки) – применение одноканальных алгоритмов с адаптацией или других упрощенных схем может выглядеть привлекательней, но это не значит, что в целевой области, которая проявится только на завершающих этапах обработки, не будут появляться артефакты. Это осложняет работу геофизика, который привык подбирать параметры обработки, ориентируясь на верхнюю часть промежуточных изображений, свободную от влияния кратных. Однако это сложность, которую надо принимать во внимание при настройке процедур, поскольку цель обработки обычно не в изучении придонных областей сред, где проблемы дискретности наблюдений особенно велики.

Литература:

1. Ампилов Ю.П. Сопоставление альтернативных технологий широкополосной морской сейсморазведки. // Технологии сейсморазведки, № 2, 2015, с.77-85.

2. Гофман П.А.., Фиников Д.Б. Подавление волн-спутников методом адаптивной рекурсивной фильтрации. // Конференция «Сейсмические технологии-2014», Москва.

3. Глоговский В.М., Фиников Д.Б. Кинематические фильтры миграционного преобразования реальных сейсмических наблюдений. // Сборник докладов третьего научного симпозиума стран-членов СЭВ по нефтяной геофизике, М., 1987.

4. Рябинский М.А., Фиников Д.Б Подавление спутника при обработке морских наблюдений. Часть 1. // Технологии сейсморазведки, № 1, 2016, с.82-92.

5. Рябинский М.А., Фиников Д.Б Подавление спутника при обработке морских наблюдений. Часть 2. // Технологии сейсморазведки, №2, 2016, с.100-108.

6. Рябинский М.А., Фиников Д.Б Подавление спутника при обработке морских наблюдений. Часть 3. // Технологии сейсморазведки, №3, 2016, с.91-101.

7. Рябинский М.А., Фиников Д.Б Многоканальные фильтры обработки морских 3D наблюдений. // Конференция «Сейсмические технологии-2015», Москва.

8. Рябинский М.А., Фиников Д.Б Обработка данных морской сейсморазведки с наклонной косой. // Конференция «Геомодель-2015», Геленджик.

9. Рябинский М.А., Фиников Д. Применение кинематических фильтров в обработке морских 3D наблюдений. // Конференция «Геомодель-2016», Геленджик.