Определение плотности зарядов для дефектов типа «трещина»

Одним из основных объектов поиска при магнитном контроле является трещина конечных размеров, имеющая выход на поверхность, так называемая поверхностная трещина. На рисунке 1 представлена тупиковая трещина, которая имеет только один выход на поверхность.

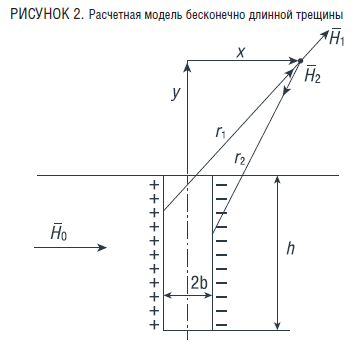
В работах (1–8) рассматривается магнитное поле рассеяния, создаваемое бесконечно длинной поверхностной трещиной, как поле, образованное двумя разноименными линейными «магнитными зарядами», имеющими равномерную линейную плотность распределения (рис. 2). Недостатком всех приведенных расчетов является то, что плотность «магнитных зарядов» на поверхностях дефектов остается неизвестной.

В [8] показано, что для линейных магнитостатических задач, в которых связь между выражается простейшей зависимостью , весьма эффективными оказываются в ряде случаев интегральные методы нахождения потенциала . Эти методы базируются на широком использовании понятия о поверхностных поляризационных зарядах. Основой их является соотношение:

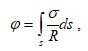
откуда следует, что при известном распределении плотности σ поляризационных зарядов на поверхности S намагничиваемого тела потенциал j последнего находится с помощью квадратур.

В связи с важной ролью величины s приведем ряд соотношений, могущих служить для ее нахождения.

Пусть поверхность S покрыта магнитными массами с плотностью s (M), являющейся функцией точки наблюдения М. нормальные составляющие напряженности результирующего поля, имеющего место в точке М с «внешней» (l) и «внутренней» (i) стороны поверхности S (рис. 3).

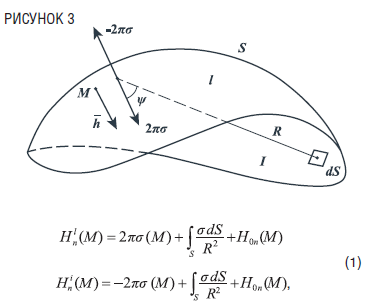
Где слагаемые ±2ps(М) представляют собой нормальные компоненты поля, непосредственно исходящего от зарядов, расположенных в ближайшей окрестности точки М на поверхности S. Вторые слагаемые определяют нормальные составляющие поля, исходящего от всех элементов поверхности S, за исключением площадки, содержащей точку М. Третьи слагаемые включают нормальные в точке М компоненты всех прочих полей. Сюда входят поля от первичных источников и поля от других заряженных поверхностей S_к, участвующих в задаче.

Рассматривая в дальнейшем поверхность S как границу раздела двух магнито-линейных сред, запишем формулу (1) в сокращенном виде:

Под здесь понимается сумма нормальных к S компонент полей от всех источников, внешних по отношению к точке М. В число последних входят источники первичных полей, а также все поверхности раздела сред с возникающими на них поляризационными зарядами («вторичные» источники), включая и ту конкретную поверхность, для которой записали уравнение (2).

Учитывая граничные условия:

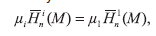
будем иметь:

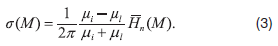
Эта формула позволяет выразить s(М) через величину 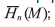называется формулой Г.А. Гринберга [9].

Формула Г.А. Гринберга используется ее автором в основном как база для построения специальных интегральных уравнений, позволяющих найти заряды s(М) на поверхностях раздела магнитно-линейных сред, если заданы первичные поля или их источники. Согласно формуле:

где Н_n(M) – результирующее поле (нормальное) к поверхности раздела сред в точке М границы;

Н_n0(M) – нормальная компонента первичного поля;

H_ns(M) – нормальная компонента поля, исходящего из всей совокупности зарядов, расположенных с плотностью s(S) по поверхности S.

Подставив (4) в (3) будем иметь следующую формулу для вычисления s:

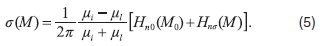
В дальнейшем будем учитывать только наведенные заряды, возникающие от первичного поля, то есть заряды 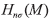первого приближения

а) Рассмотрим трещину конечных размеров, находящихся в однородном магнитном поле Н₀:

Для определения Н_ns выделим на поверхности 1 площадку dS = dydz, тогда dm = sdydz, где s плотность распределения магнитных зарядов на поверхности 1. Эти заряды вызывают на поверхности 2 новое распределение поля Н_ns, которое мы определим следующим образом. Возьмем произвольную точку А (-b, y₀, z₀) на поверхности 2, выделим вокруг нее элементарную площадку dS. Заряд в точке А будет равен: dm = sdy₀dz₀. На поверхности 2 выберем произвольную точку М (b, y, z). Далее определим dН(М) от заряда dm из точки А.

Рис. 5.

Из рисунка 5 следует:

Подставив получим:

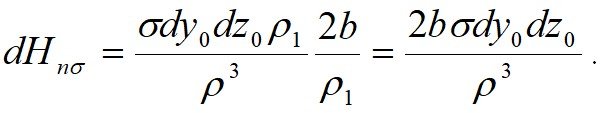
Получившийся интеграл имеет очень сложный вид, если обозначить его через I (y, z), то получим следующее выражение:



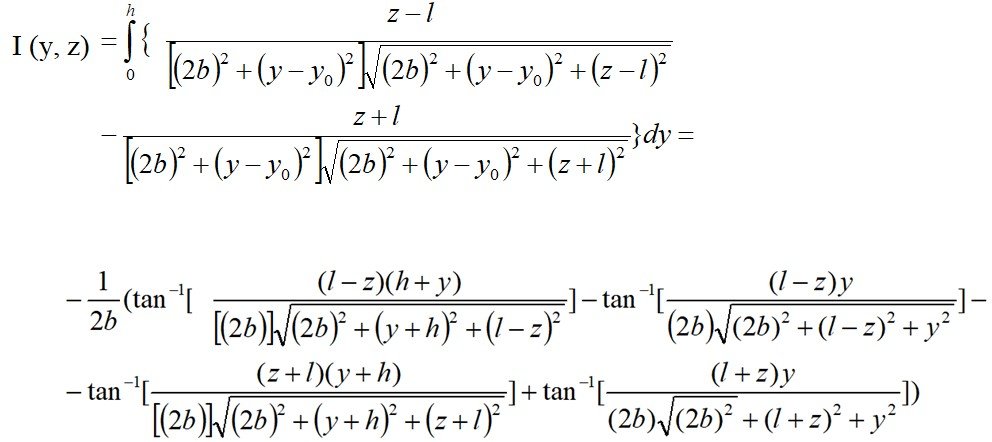
здесь
Итого получим:

И воспользовавшись формулой Г.А. Гринберга будем иметь:




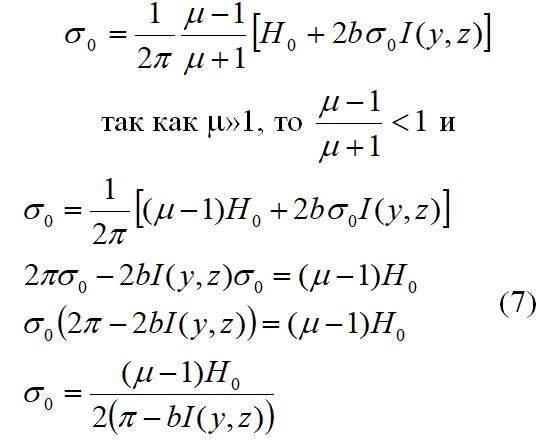
Если в формуле (6) , т.е. рассмотреть бесконечно длинную трещину, т.е.:



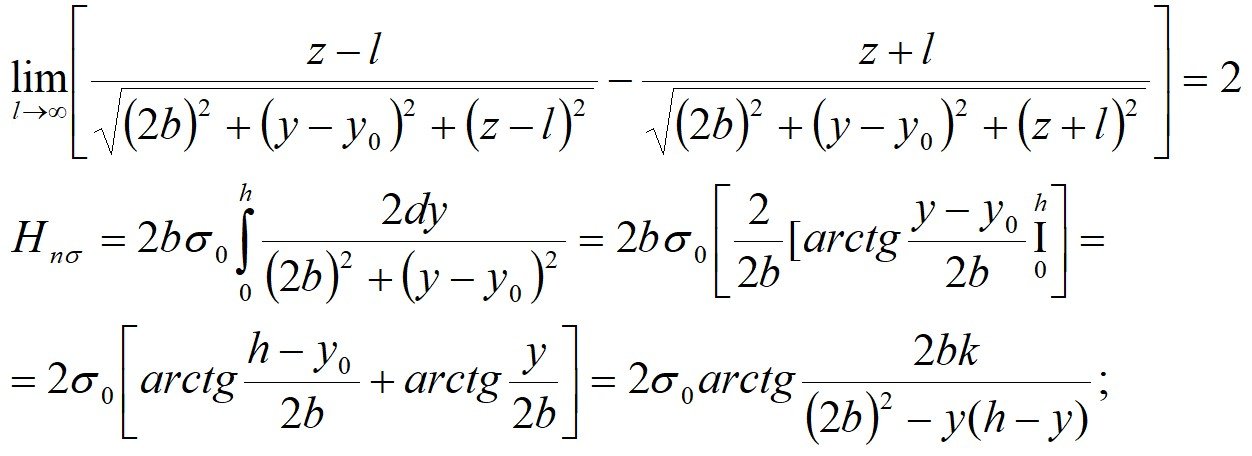
И из формулы Г.А. Гринберга (9):




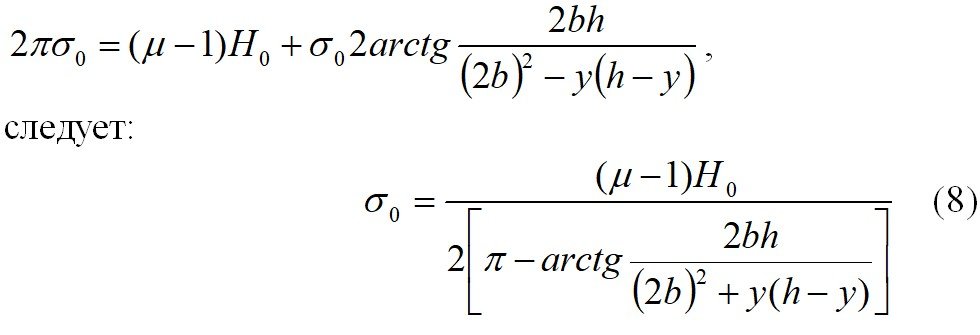
Для примера построим распределение (y) бесконечно длинной трещины глубиной 5 мм, шириной раскрытия 0,1мм, H₀ = 10ка/м (рис. 6).



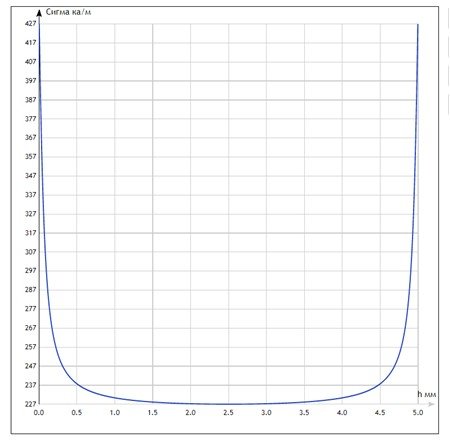
РИС. 6.
Распределениепри=10кА/м, h = 5мм

Данные расчета приведены в таблице 1.

Таблица 1



Формулы для определения распределения магнитных зарядов на гранях дефекта тапа «трещина» (бесконечно длинный дефект) были получены в работах (1–7):

Ф. Ферстера (1)



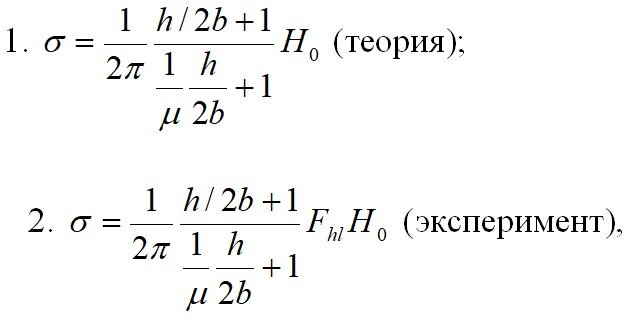
где
= 2,65 – так называемый нелинейный фактор, введенный автором для более удовлетворительного совпадения теории с экспериментом.

h – глубина дефекта, 2 b – ширина дефекта,
– магнитная проницаемость, – напряженность магнитного поля.

2. Щербинина В.Е (4)



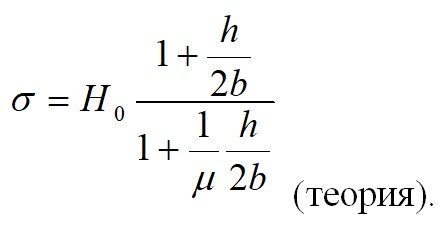
3. Пошагина А.И. (3, 7)



4. Сапожникова А.Д. (5)

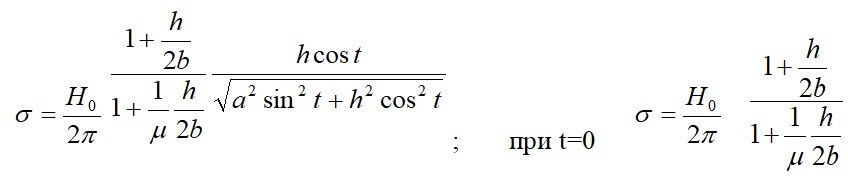
t – угол, образованный подвижным радиусом r c осью ох (малая ось эллипсоида).

5. Мужицкого В.Ф. (6)



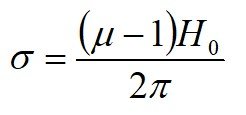
6. Шура М.Л. (2)


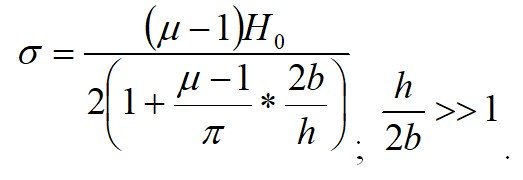
Для сравнения вышеприведенных формул между собой возьмем для примера конкретную трещину со следующими параметрами:




Из сравнения получаем, что наиболее близкое значение (см. рис. 6) дает формула Мужицкого В.Ф., поэтому в дальнейших расчетах принимаем:




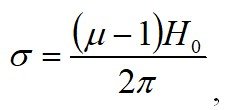
при этом ошибка составляет 0,26 %.

Литература

1. Forster F. Neue Erkentnisse auf dem Gebiet der zerstorungsfreien Priifung mit magnetischen streu fluss. – 3-rd European Conference on NDT. Florence (15–18 Oktober, 1984), Conf. Proc. Techn., vol. 5, p. 287–303.

2. Дефектоскопия, 1988, № 3, с. 14–25, М.Л. Шур, Р.В. Загидулин, В.Е. Щербинин Теоретические вопросы формирования поля поверхностного дефекта.

3. Пашагин. А.И. Определение параметров дефекта типа прямоугольной щели по величине тангенциальной компоненты его магнитного поля. – Деп. № 715–В. 93. – М.: ВИНИТИ, 1993.

4. Щербинин В.Е., Пашагин А.И. О поляризации трещины при неоднородном намагничивании изделия. – Дефектоскопия, 1974, № 3, с. 17–23.

5. Сапожников А.Д. Теоретические основы электромагнитной дефектоскопии металлических тел, том 1, Издательство Томского университета, Томск 1980 г.

6. Мужицкий В.Ф. Модель поверхностного дефекта и расчет топографии его магнитостатического поля – Дефектоскопия, № 10, 2003, с. 3–17.

7. Пашагин А.И., Бенклевская Н.П., Щербинин В.Е. Магнитное поле дефекта внутри его полости и вблизи поверхности изделия – Дефектоскопия, 1996, № 8, с. 30–38.

8. А.Б. Сапожников Теоретические основы электромагнитной дефектоскопии металлических тел (том 1, Томск, 1980 г.)

9. Г.А. Гринберг. Избранные вопросы математической теории электрических и магнитных явлений (Москва, издательство АН СССР, 1948 г.).

10. И.Н. Бронштейн, К.А. Семендяев. Справочник по математике (Москва, 1957 г.).