Ключевые слова: потеря устойчивости, продольный изгиб, наклонно-направленное бурение, напряженно-деформированное состояние, бурильная колонна, вибрация, динамические условия.
Современное строительство нефтяных и газовых скважин осуществляется за счет механического вращательного бурения. Вращение породоразрушающего инструмента за счет верхнего силового привода или забойного двигателя с некоторой осевой нагрузкой, вызывающее ответную силу реакции со стороны забоя скважины, приводит к разрушению горной породы и проходке ствола. В связи с наличием осевой нагрузки низ бурильной колонны испытывает нагрузку сжатия. В наклонно-направленных скважинах, скважинах с горизонтальным окончанием, скважинах с большим отходом от вертикали сжимающая нагрузка может воздействовать на участок бурильной колонны значительной протяженности и при превышении критической нагрузки формируется продольный изгиб колонны от потери прямолинейной формы устойчивости. Инструмент в таком состоянии формирует значительные боковые силы, вследствие чего на производстве есть риск запирания инструмента и недохождения осевой нагрузки до долота с одновременным снижением или отсутствием механической скорости проходки. Вращение инструмента, потерявшего прямолинейную форму устойчивости, приводит к возникновению циклических знакопеременных нагрузок, то есть к повышенному усталостному износу. Поэтому в большинстве случаев рекомендуется не допускать образование синусоидального и тем более спирального изгиба бурильной колонны.
Знание о фактической деформации инструмента, в том числе о продольном изгибе, важно с позиции понимания распределения нагрузок и моментов по бурильной колонне и моделирования напряженного состояния бурильного инструмента в целях прогнозирования его прочности и долговечности. Выполнить такой прогноз на основе существующих аналитических моделей в реальных наклонно-направленных скважинах невозможно с высокой точностью. Это связано с неопределенностями в процессе бурения – шероховатость стенок скважины, извилистость ствола, кавернозность, коэффициенты трения – и с несовершенством теоретических моделей.
После произошедшей потери прямолинейной формы устойчивости внутрискважинного инструмента происходит перераспределение нагрузок по всей колонне, поэтому идентификация данного события важна для оценки и обеспечения прочности и долговечности инструмента, а также своевременных действий по корректировке технологических параметров бурения в целях обеспечения максимальной скорости проходки без осложнений при наименьшей затраченной энергии. Очевидно, что в большинстве случаев формирование продольного изгиба – вредное явление, забирающее на себя часть подводимой для разрушения горных пород энергии.
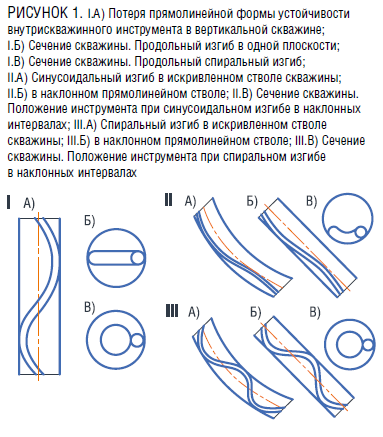
В первую очередь вследствие продольного изгиба на инструмент будет воздействовать изгибающий момент (рис. 1) [7, 8]. Потеря прямолинейной формы устойчивости в первоначальной своей стадии выглядит как синусоидальный продольный изгиб (рис. 1.I.Б, рис. 1.II), который при последующем подводе массы верхней части колонны бурильных труб, то есть при росте сжимающей нагрузки, перейдет в форму спирального изгиба (рис. 1.I.В, рис. 1.III).
Изменение осевой силы по колонне труб можно определить по формуле 1. Сумма изменения осевой силы по колонне труб и нагрузки на долоте, а также эффекта от гидравлического давления позволит определить вес на крюке.
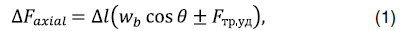
где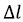 
– рассматриваемый интервал изменения осевой силы, м;
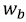– погонный вес инструмента с учетом облегчения в буровом растворе, Н/м;
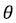– зенитный угол, который можно принять в качестве среднего арифметического на интервале 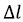, град;
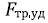– удельная сила трения на интервале 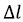, Н/м.
Знак удельной силы трения зависит от направления движения инструмента. Знак минус выбирается при спуске инструмента или бурении, знак плюс – при подъеме инструмента или обратной проработке.
Изменение крутящего момента по колонне труб можно определить по формуле 2. Сумма изменения крутящего момента по колонне труб и момента на долоте, а также сопротивления на вращение колонны в вязкой среде бурового раствора позволит определит крутящий момент на роторе (верхнем силовом приводе).
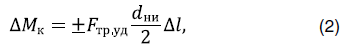
Где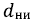 
– наружный диаметр инструмента на интервале 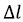, м. Знак удельной силы трения зависит от места приложения и направления действия момента. При бурении с вращением всей колонны берется знак плюс, при бурении с забойным двигателем берется знак минус для учета затухания реактивного момента от забойного двигателя по стволу скважины.
Удельная сила трения может быть определена по формуле 3.
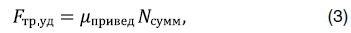
Где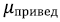 
– коэффициент трения на участке ;
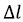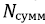– боковые силы взаимодействия бурильного инструмента и стенки скважины.
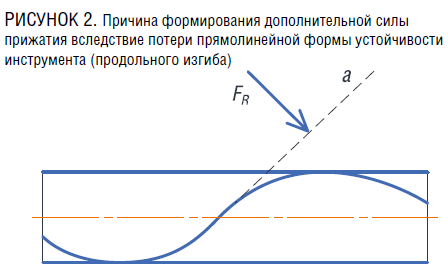
В результате формирования продольного изгиба образуется дополнительное прижатие инструмента к стенке скважины (рисунок 2) [1]. Дополнительное прижатие формируется из-за того, что стенки скважины стремятся вернуть инструмент (линия а на рис. 2) во внутрискважинное пространство с некоторой силой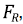 
как показано на рисунке. Со стороны инструмента формируется ответная реакция, приводящая к росту боковой силы взаимодействия бурильной колонны и стенки скважины, а значит и удельной силы трения. Таким образом, во вторую очередь вследствие возникновения продольного изгиба происходит перераспределение растягивающей силы (формула 1) и крутящего момента (формула 2) по стволу скважины.
В процессе бурения бурильная колонна находится в динамических условиях, то есть возникают вибрации. Особенности перекатывания шарошек у шарошечных долот порождают осевые колебания, эксцентриситет рабочего ротора и статора винтового забойного двигателя или несовершенство литья турбин турбобура порождают боковые колебания, а периодическое заклинивание долота на забое или инструмента над забоем при их вращении с последующим их резким освобождением порождают крутильные колебания [2].
Авторами данной статьи сделано предположение, что из-за совокупности причин критическая нагрузка у бурильного инструмента может быть снижена и возможна преждевременная потеря прямолинейной формы устойчивости при наличии вибраций бурильной колонны (БК). Цель данной статьи – разработать методику исследования потери прямолинейной формы устойчивости модели бурильной колонны в динамических условиях и подтвердить выдвинутую гипотезу.
Методы
Перед разработкой методики исследования влияния разноамплитудных и разночастотных колебаний на потерю прямолинейной формы устойчивости бурильной колонны следует определить из какого материала и какого диаметра необходимо использовать модели бурильной колонны при проведении экспериментов.
В первую очередь будет использована формула Эйлера для определения критической силы для стержня определенной длины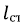 
:
Где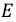 
– модуль упругости, Па;
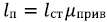– приведенная длина стержня, м;
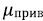– коэффициент приведения заданной длины стержня к длине полуволны его изгиба в критическом состоянии;
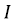– осевой момент инерции, в плоскости которого наиболее вероятен изгиб, . Осевой момент инерции для формы поперечного сечения в виде круга определяется по формуле 5, в виде кольца – по формуле 6.
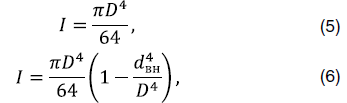
Где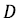 
– наружный диаметр прутка или трубки, м;
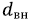– внутренний диаметр трубки, м.
В расчетах были рассмотрены два сплава: латунь Л63 с модулем упругости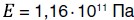 
и алюминий АД31 с модулем упругости 
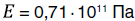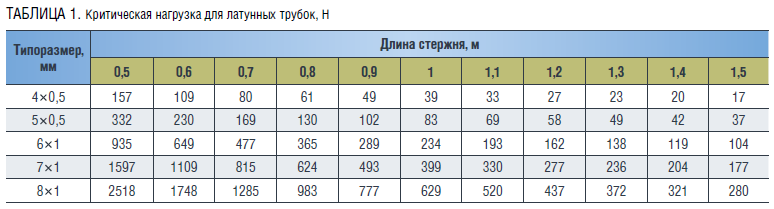
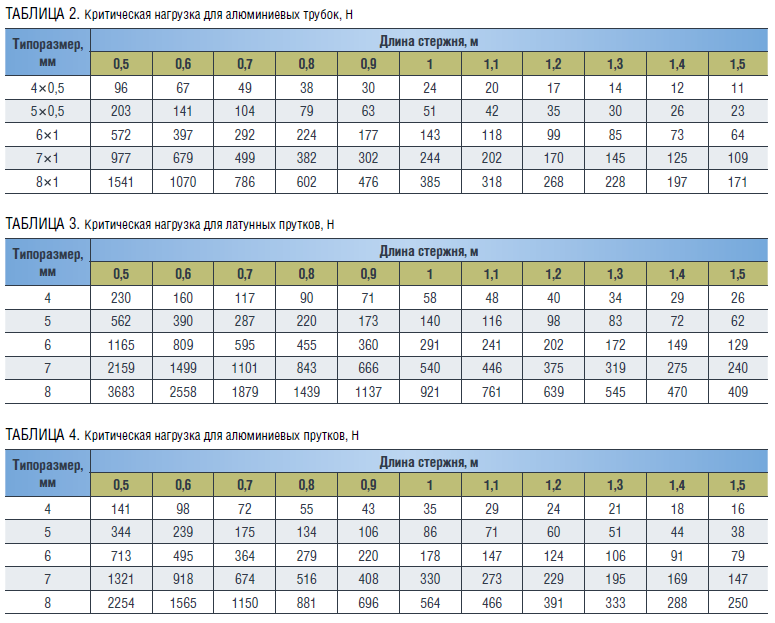
. Коэффициент приведения длины принимается равным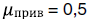 
. В разрабатываемой методике предполагается использовать трубки и прутки. Результаты расчета представлены в таблицах 1–4.
Критическая сила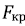 
, определенная по формуле 4, обозначает, что такую сжимающую нагрузку необходимо создать на стержень приведенной длины 
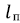, чтобы вывести его из прямолинейной формы устойчивости. По мере нагружения стержня прогиб его будет увеличиваться. Из-за наличия ограничивающего цилиндра (стенок скважины) при касании стержня (бурильной колонны) стенок продольный изгиб в одной плоскости перейдет в спиральную форму при дальнейшем нагружении. Поэтому при проведении экспериментов необходимо предусмотреть применение трубки, имитирующей ствол скважины, диаметр которой должен соответствовать геометрическому подобию отношения диаметра внутрискважинного инструмента к диаметру ствола скважины. Наиболее часто используемые бурильные трубы 127 мм могут быть в составе бурильных колонн при бурении интервалов различного диаметра: от 212,7 до 393,7 мм, в таком случае критерий подобия составит от 0,597 до 0,323 соответственно.
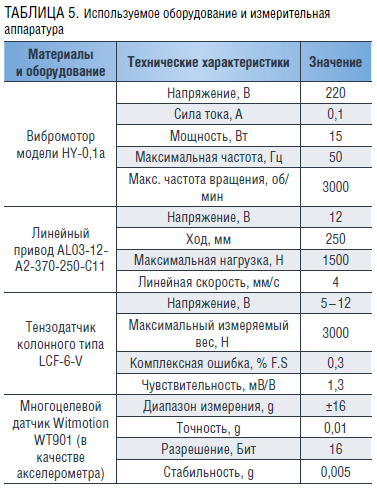
В лабораторном фонде Санкт-Петербургского горного университета императрицы Екатерины II имеются буровые установки, однако расчеты критической нагрузки для латунных и алюминиевых стержней диаметром 4–8 мм, планируемых к использованию в качестве модели бурильной колонны, показывают, что их применение излишне. Достаточно нагружателя или привода, способного создавать нагрузку до 1500 Н (таблица 5).
Методика исследования влияния вибрации на потерю прямолинейной формы устойчивости, представленная в статье, осуществляется следующим образом. Производится калибровка тензодатчика и акселерометра перед проведением серий циклов нагружения–разгружения стержня. После стержень устанавливается внутрь трубки из оргстекла, имитирующей ствол скважины, и за счет выдвижения платформы, на которую опирается стержень, штоком привода подводится до верхнего упора без деформации.
Проводится серия циклов нагружения–разгружения стержня без вибрационного воздействия. Нагружение–разгружение стержня производится в диапазоне деформации согласно заранее нанесенным рискам на стержне с помощью актуатора, рассчитанного на максимальную нагрузку в 1500 Н. Нижняя риска доходит до низа ствола скважины при сжатии, верхняя – при разгрузке. Положение нижней риски внизу ствола скважины соответствует четырем – трем полуволнам, образуемым стержнем, в зависимости от диаметра и материала используемого стержня. Под полуволной понимается поворот спирали на 180°, так как после первого касания моделью бурильной колонны стенки скважины наблюдается характер спирального изгиба. В процессе нагружения–разгружения тензодатчик фиксирует изменение сжимающей нагрузки, действующей на стержень по мере его деформации от выдвижения штока актуатора.
Включается акселерометр и вибромотор. При заданной частоте вращения вибромотора проводится серия циклов нагружения–разгружения. В процессе нагружения–разгружения тензодатчик фиксирует изменение сжимающей нагрузки, акселерометр фиксирует виброускорения в трех осях Ox, Oy, Oz. Из-за вращения эксцентриков вибромотора в одной плоскости вибрации должны действовать по двум осям Oz, соответствующей оси модели бурильной колонны, и в оси Oy, то есть формируя поперечные колебания для модели БК.
Результаты
На рисунке 3 представлены данные, зафиксированные тензодатчиком в ходе серии циклов нагружения–разгружения стержня без вибрационного воздействия, на рисунке 4 – данные серии циклов нагружения–разгружения с одним из уровней вибрационного воздействия.
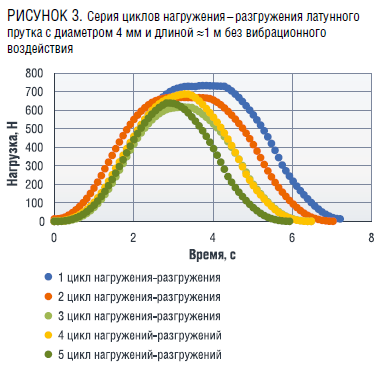
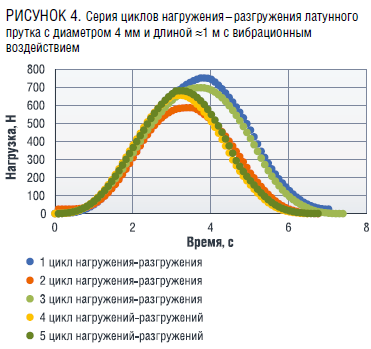
Производится обработка результатов эксперимента. На примере графиков из рисунков 3–4 были определены производные функций изменения нагрузки от времени на линейных участках путем линейной аппроксимации, как показано на рисунке 5 и представлено в табличной форме (таблица 6).
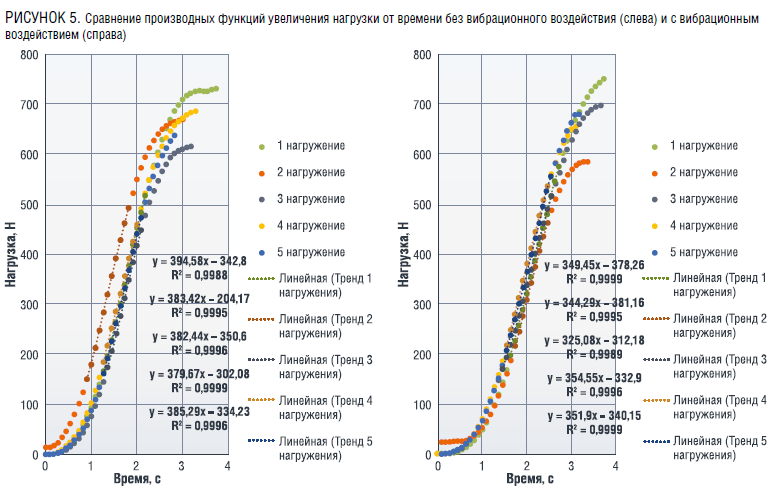
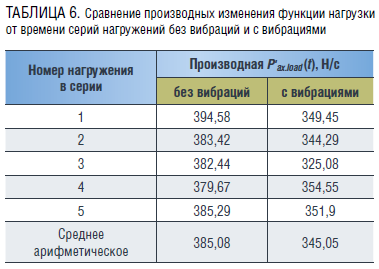
Таблица 6 показывает, что с рассматриваемым уровнем вибрационного воздействия среднее арифметическое производной всех циклов нагружения серии меньше на 10,4 %, чем без него. Снижение значения производной наблюдается для проведенных серий циклов нагружения–разгружения с другими уровнями вибрационного воздействия, что подтверждает влияние вибраций на продольный изгиб модели бурильной колонны.
Обсуждение
В ходе эксперимента было обнаружено, что стержень, модель БК, изгибается в одной плоскости только до момента касания стенок модели ствола скважины. После касания начинают формироваться две «полуволны» и наблюдается характер спирального изгиба.
После этого момента, когда стержень начнет создавать боковую нагрузку на стенку скважины, и далее вследcтвие малого диаметра модели ствола скважины, то есть трубки из оргстекла с наружным диаметром 16 мм и толщиной стенки 2 мм, она может изгибаться, поэтому в приведенной методике используются дополнительные ребра жесткости.
Формирование спирального изгиба связано с характером геометрии ограничивающих продольный изгиб условий, а именно цилиндрической стенки скважины. Для прогнозирования нагрузки, образовавшей спиральный изгиб бурильной колонны (модели) с определенным шагом винтовой линии (длиной «волны») p, в вертикальном стволе (модели ствола) можно воспользоваться формулой (7) [3]:
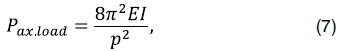
Во время проведения эксперимента стало очевидным, что при прижатии модели бурильной колонны к стенке скважины должны формироваться силы трения, что ранее и описывалось в статье, поэтому, как и отмечается авторами различных трудов, в формуле 7 корректнее было учитывать наличие сил трения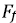 
, возникающих от формирования дополнительной силы прижатия (формула 8) [6]:
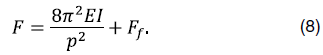
Стоит обратить внимание, что в формулах 9–10 и 13–14, часто используемых в производстве, не учитывается влияние сил трения [5].
Критическая сила, приводящая к началу формирования синусоидального изгиба бурильной колонны в искривленном стволе скважины:
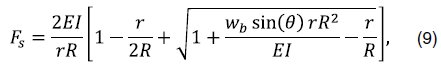
где r – радиальный зазор между бурильным инструментом и стенкой скважины, м; R – радиус искривления ствола скважины, м.
Критическая сила, приводящая к формированию спирального изгиба бурильной колонны в искривленном стволе скважины:
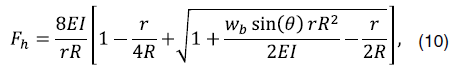
Если раскрыть скобки и принять, что радиус изгиба равен бесконечности (формулы 11–12), то можно получить соответствующие формулы критических нагрузок для наклонных прямолинейных стволов
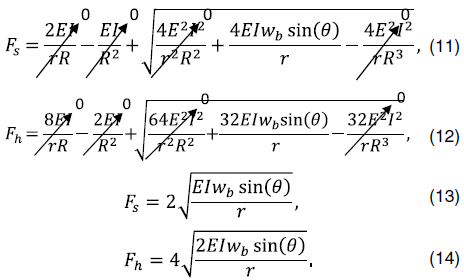
Существуют научные труды, в которых авторы подтверждают влияние силы трения на критическую нагрузку синусоидального и спирального изгибов [4]. В ссылаемом научном труде снижение сил трения осуществлялось за счет создания вибраций на ограничивающую изгиб стержня трубки, то есть модели ствола скважины. В нашей разрабатываемой методике вибрации создаются на платформе, сжимающей стержень, как будто бы источником вибраций является КНБК и бурильная колонна. Стоит обратить внимание, что вибрации практически всегда присутствуют при бурении, что не учитывается авторами ссылаемой статьи. В проведенных нами экспериментах рассматривается случай, когда модель бурильной колонны не вращается, что справедливо при бурении с забойными двигателями. При бурении с забойными двигателями могут формироваться поперечные колебания от эксцентриситета ротора и статора ВЗД или неточности литья турбинок турбобура, так и продольные колебания при разрушении горной породы шарошечными долотами. Таким образом, мы, авторский коллектив, предполагаем, что первый механизм снижения критический нагрузки от влияния вибрации связан со снижением сил трения между бурильным инструментом и стенкой скважины, что особенно актуально учитывать в наклонных и искривленных стволах, а также при уже образовавшемся продольном изгибе с прижатием к стенкам скважины и последующем нагружении бурильной колонны. Второй механизм снижения критической нагрузки предполагаемо связан с наличием начального эксцентриситета, мгновенного прогиба колонны от воздействия вибраций, облегчающего формирование дальнейшего продольного изгиба при нагружении. Третий механизм предполагаемо связан с образованием повышенных мгновенных сил и моментов: поперечных от воздействия поперечных вибраций, осевых от воздействия осевых вибраций и крутящего момента от крутильных колебаний. Влияние крутящего момента не рассматривается в текущей статье.
В статье рассматривалось изменение нагрузки во времени. Более информативный результат можно получить при построении графиков нагрузки от степени выдвижения штока актуатора, то есть линейной деформации модели бурильной колонны относительно ее оси. Для этого в разработанную методику следует добавить использование датчика положения штока и программно управляемый привод.
С учетом приведенных выше размышлений для оценки влияния вибраций на потерю устойчивости можно предложить следующую методику проведения эксперимента:
1. Стержень при выключенном вибромоторе, то есть в статических условиях, нагружается вплоть до спирального изгиба с несколькими «полуволнами» (полуспирали).
2. При выдвижении штока на требуемую длину осуществляется разгрузка со снятием упругих деформаций изгиба.
3. Во время цикла нагружения–разгружения производится замер веса тензодатчиком и строится зависимость веса на тензодатчике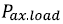 
от хода линейного привода 
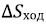или от времени проведения эксперимента, производится несколько опытов нагружения–разгружения для повышения точности проведения эксперимента.
4. Производится повторная серия циклов нагрузки–разгрузки стержня при включенном вибромоторе с постоянным виброускорением и частотой вращения эксцентриков вибромотора с замером виброускорения по акселерометру и веса на тензодатчике.
5. Производится несколько циклов нагрузки–разгрузки при разной частоте вращения вибромотора.
6. Сравниваются графики зависимости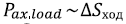 
при разных значениях виброускорения G и частоты колебаний V.
Выводы
1. Разрабатываемая система мониторинга напряженно-деформированного состояния БК должна учитывать и нивелировать неопределенности бурения и несовершенства аналитических моделей.
2. Аналитические модели определения критической нагрузки, ровно как прогнозирование деформации инструмента от продольного изгиба, до сих пор остаются несовершенными, но не учитывающими влияние сил трения между бурильной колонной и стенками скважины, вращения бурильной колонны, крутящего момента, действующего на внутрискважинный инструмент, и вибрации, то есть нахождение модели математической модели бурильной колонны в динамических условиях.
3. Система прямых измерений не требует применения аналитических моделей. Второй способ реализации систем мониторинга через аналитические модели и анализ косвенных факторов требует дальнейшей доработки аналитических моделей и адаптации под условия бурения, то есть использование конкретной модели под конкретные условия или события.
4. Разработана методика оценки влияния вибраций на потерю прямолинейной формы устойчивости бурильной колонн.
5. Было обнаружено, что вибрации влияют на поведение инструмента при продольном изгибе и снижают критическую нагрузку.
6. Необходимо и далее проводить исследования в данном направлении, в том числе в исследовании потери устойчивости бурильной колонны в динамических условиях: получение зависимостей изменения нагрузки от осевого смещения модели БК с учетом вибрационного воздействия, крутящего момента и крутильных колебаний, вращения модели БК.
Литература
1. Кирсанов А.Н. Буровые машины и механизмы / А.Н. Кирсанов, В.П. Зиненко, В.Г. Кардыш. – М.: Недра, 1981. – 448 с.
2. Aarsnes U.J.F. Estimating friction factors while drilling / U.J.F. Aarsnes, J. Auriol, F.D. Meglio et al. / Journal of Petroleum Science and Engineering. – 2019. – Vol. 179, № January. – P. 80–91. DOI: 10.1016/j.petrol.2019.04.014.
3. Lubinski A. Helical Buckling of Tubing Sealed in Packers /A. Lubinski, W.S. Althouse/ Journal of Petroleum Technology. – 1962. – Vol. 14, № 06. – P. 655–670. DOI: 10.2118/178-PA.
4. McCann R.C. Experimental study of curvature and frictional effects on Buckling / R.C. McCann, P.V.R. Suryanarayana / Proceedings Annular Offshore Technology Conference. – 1994. – P. 511–521. DOI: 10.4043/7568-MS.
5. Qiu W. Drill pipe/coiled tubing buckling analysis in a hole of constant curvature / W. Qiu, S. Miska, L. Volk / Proceedings Permian Basin Oil Gas Recovery Conference. – 1998. – P. 385–389. DOI: 10.2118/39795-MS.
6. Tan X.C. Buckling of slender string in cylindrical tube under axial load: Experiments and theoretical analysis / X.C. Tan, B. Forsman / Experimental Mechanics. – 1995. – Vol. 35, № 1. – P. 55–60.
7. Zhang Q. Post-buckling transition of compressed pipe strings in horizontal wellbores / Q. Zhang, J. Wiang, W. Cui et al. / Ocean Engineering. – 2020. – Vol. 197, № November 2019. – P. 106880. DOI: 10.1016/j.oceaneng.2019.106880.
8. Zhu Z.L. Buckling behavior and axial load transfer assessment of coiled tubing with initial curvature in an inclined well / Z.L. Zhu, Z. Liang, Y.Hu / Journal of Petroleum Science and Engineering. – 2019. – Vol. 173, № August 2018. – P. 136–145. DOI: 10.1016/j.petrol.2018.10.021.
