При разработке газовых и газоконденсатных месторождений одной из важнейших является задача планирования технологических режимов работы добывающих скважин. Общий дебит газа месторождения необходимо распределить между отдельными скважинами с учетом графика проводимых геолого-технических мероприятий (ГТМ), связанных с остановкой отдельных скважин. Для выполнения плана добычи остановка одних скважин требует повышения дебита на других. В случае газовых месторождений обычно исходят из возможностей повышения дебитов оставшегося в работе фонда скважин в пределах допустимых значений. Диапазон возможных дебитов скважин определяется рядом факторов: ограничениями по предельной депрессии, минимальному дебиту, обеспечивающему вынос жидкости с забоя, минимизацией абразивного износа труб, недопущение гидратообразования и пр. В случае газоконденсатных месторождений появляется дополнительный фактор – содержание конденсата в добываемой продукции.
Отличительной особенностью разработки газоконденсатных месторождений является ретроградная конденсация и выпадение из газа тяжелых углеводородных фракций С5+ в пласте при снижении давления ниже порогового значения [3]. Это ведет к потерям ценных компонент, поскольку подвижность жидкого конденсата в пласте невелика, и он после выпадения становится практически неизвлекаемым. Величина потерь конденсата напрямую зависит от величины падения давления в пласте. Наиболее низким давление оказывается в окрестностях забоев добывающих скважин, что приводит к активному выпадению конденсата вблизи скважин. Полностью избежать таких потерь невозможно, однако, варьируя режимы работы скважин, можно уменьшить их величину. Повышение дебита скважин сопровождается падением их забойного давления и, как следствие, дополнительными ретроградными потерями конденсата в пласте и наоборот. Потери конденсата зависят от состояния призабойной зоны, текущего пластового давления и индивидуальны для каждой скважины. Это ведет к зависимости итогового содержания конденсата в продукции от способа распределения добычи газа между скважинами. Подбор оптимального распределения добычи газа, имеющего максимальное содержание конденсата позволяет снизить потери конденсата и повысить его текущую добычу. Такой способ снижения потерь в добыче конденсата за счет оптимизации технологического режима не требует дополнительных инвестиций и может быть использован на любом газоконденсатном месторождении. Алгоритмы поиска оптимальных режимов работы скважин существенно зависят от сложности используемой математической модели добычи, типа используемой информации о пластовой системе. Использование быстрых алгоритмов и методов расчета оптимальных технологических режимов, позволяет в режиме реального времени планировать работу скважин, добиваясь повышения экономических показателей. Поэтому их разработка представляет собой актуальную задачу.
Укрупненные математические модели добычи газа и конденсата
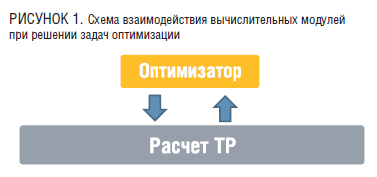
Традиционно решение задач оптимизации основано на некотором методе расчета параметров технологического режима (ТР). При этом модуль оптимизации периодически обращается к модулю расчета ТР, меняя в нем управляющие параметры и получая в ответ результаты расчета ТР. Скорость нахождения оптимального решения при этом существенно зависит от скорости работы модуля расчета ТР.
Отличительной особенностью работы газовых и газоконденсатных месторождений является фонтанный (бескомпрессорный) способ добычи, при котором дебиты скважин одновременно зависят от состояния пластовой системы и от параметров газосборной системы (ГСС): сопротивлений труб, схемы их соединения и диаметров штуцеров [2]. Иначе говоря, пласт, скважины и ГСС в этом случае образуют единую взаимосвязанную систему. Ее полноценный расчет требует применения т.н. интегрированной модели (ИМ), включающей в себя пластовую систему, скважины и ГСС. Каждый элемент такой системы описывается системой уравнений в частных производных (УЧП), что предопределяет высокую продолжительность и сложность расчета и адаптации подобной системы. Другим немаловажным аспектом применения подобных систем является высокий объем входной информации и чувствительность к ее точности. Отсутствие достоверной информации по отдельным элементам и замена ее на приближенную приводит к значимым изменениям в результатах моделирования. Все это не позволяет использовать ИМ в задачах оперативного прогнозирования технологического режима и тем более в задачах краткосрочной оптимизации. Естественным способом обойти вышеуказанные проблемы является подход с использованием укрупненных моделей добычи газа. При этом в первую очередь отказываются от детализации поведения пласта [6], а притоки газа к скважинам описывают аналитическими уравнениями, например вида [8]
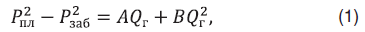
где Pпл – пластовое давление, Pзаб – забойное давление, Qг – дебит газа. Коэффициенты фильтрационного сопротивления А и В рассчитываются по результатам газодинамических исследований скважин (ГДИС) или могут быть аналитически выражены через его фильтрационно-емкостные характеристики [2]. Пластовое давление при этом восстанавливается по результатам замеров забойного (устьевого) давления или рассчитывается в рамках упрощенной модели материального баланса. Содержание конденсата в добываемой продукции описывается конденсатно-газовым фактором (КГФ)
где Qк – дебит конденсата.
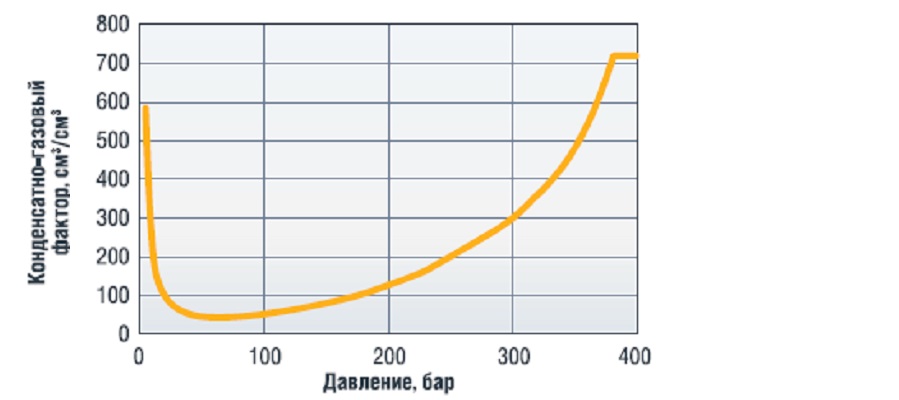
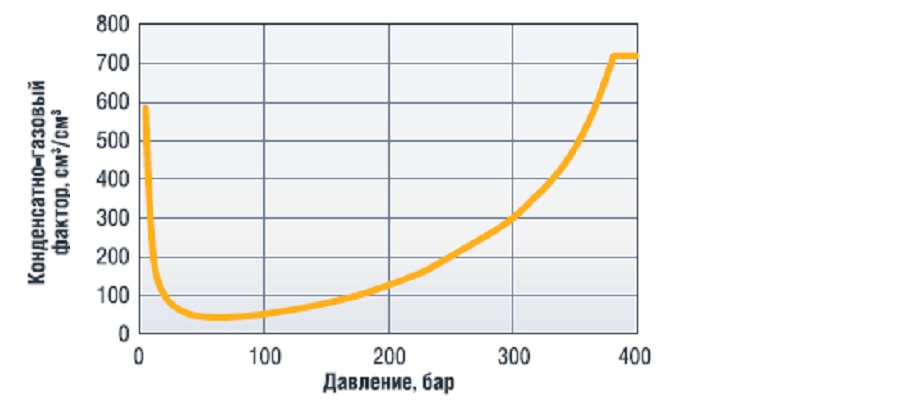
Вид зависимости КГФ от давления и температуры определяется по результатам скважинных газоконденсатных исследований (ГКИ), совмещенных с ГДИС либо расчетным методом, исходя из состава газа. Пример такой зависимости при постоянной температуре приведен на рисунке 2
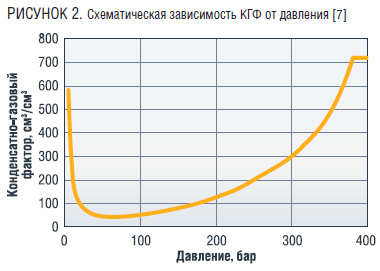
Вторым шагом упрощения модели является переход к аналитическим моделям работы скважин и элементов ГСС [6, 10].
Если ГСС содержит n-скважин, m-поверхностных участков ГСС и k-узлов, в которых соединяются участки ГСС, то система уравнений будет содержать n-уравнений притока к скважинам, n-уравнений потерь давления потока в стволах скважин, n-уравнений потерь давления в штуцерах на устье скважин, n-уравнений расчета средних температур в стволах скважин, n-уравнений расчета КГФ, m-уравнений потерь давления по каждому из участков ГСС, m-уравнений расчета средних температур на участках ГСС, 3k-уравнений сохранения энергии и массы газовой и жидкой фаз в узловых точках соединения участков ГСС. Система замыкается (n+m)-уравнениями состояния газа, которые будут иметь отличные коэффициенты для каждой скважины и элемента ГСС. Таким образом, общее количество уравнений составит 6n+3m+3k, что может составлять более ста. Как показывает практика, расчет подобной системы происходит достаточно быстро и может быть использован при решении задач оптимизации [6, 10].
Вместе с тем нельзя не отметить, что в практике расчетов ТР нашли широкое применение различного рода коммерческие симуляторы работы ГСС (например, Pipesim, GAP и пр). В них производится численный расчет УЧП потоков фаз в трубных элементах ГСС для определения стационарных распределений давлений, скоростей фаз и температур. Время расчета напрямую зависит от сложности ГСС, степени измельчения участков и не превышает нескольких минут. Это позволяет повысить точность прогнозирования параметров ТР и использовать их в задачах краткосрочной оптимизации добычи при неизменном составе продукции добывающих скважин. В случае газоконденсатных месторождений состав добываемой продукции зависит от забойного давления вследствие ретроградных потерь в пласте. Данное обстоятельство не позволяет напрямую использовать подобные симуляторы для определения ТР с минимальными потерями конденсата. При решении такой задачи выстраивается итерационный процесс, в котором производится последовательное изменение состава газа, что занимает уже весьма продолжительное время. Вместе с тем возможен и альтернативный подход, основанный на прямом решении задачи минимизации пластовых потерь конденсата с исключением из него расчета давлений в ГСС и диаметров штуцеров.
Задача краткосрочной оптимизации
При краткосрочной оптимизации прогнозируется работа скважин в течение одного-двух месяцев. В таком случае влиянием изменения режима одних скважин на другие в течение прогнозного периода можно пренебречь. Фактически принимается концепция последовательной смены состояний, при которой изменения в состоянии пластовой системы на текущем шаге невелики и учитываются на следующем прогнозном шаге. Задача краткосрочной оптимизации обычно формулируется в виде максимизации текущей добычи конденсата при заданном уровне добычи газа
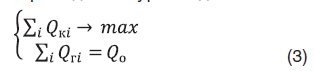
где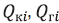
– дебиты конденсата и газа отдельных скважин; 
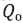–заданный уровень добычи газа. Что эквивалентно максимизации содержания компонентов С5+
в продукции (максимизации КГФ). Т.к. снижение содержания С5+ определяется ретроградными потерями конденсата в пласте, то задача оптимизации сводится к минимизации этих потерь. Как следует из рисунка 2, значение КГФ зависит от давления и своего минимального значения в пласте достигает в призабойных зонах скважин. Можно принять, что величина КГФ газа, приходящего на забой скважины, определяется уровнем Pзаб. В таком случае система уравнений, определяющих дебит газа и конденсата на скважинах, принимает вид:
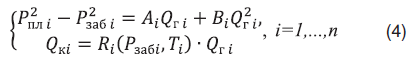
Используя первое из уравнений (4), можно выразить Pзаб i в явном виде и исключить его из второго уравнения. При условии постоянства температуры Т i дебит конденсата будет зависеть только от дебита газа. Тогда система (4) примет вид
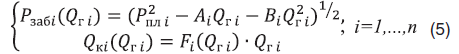
где принято
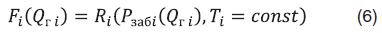
Задача оптимизации (3) принимает вид
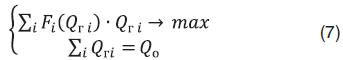
Отметим, что для решения задач (3) и (7) не требуется расчет параметров ГСС. Задача (7) представляет собой задачу нелинейной оптимизации в пространстве n-переменных . Целевая функция имеет сложную нелинейную зависимость от аргументов, что делает возможным решение только численными методами [4].
Аналитические методы решения задачи краткосрочной оптимизации
Если отсутствует взаимное влияние скважин друг на друга, то оптимальное решение задач (3) и (7) обладает свойством быть одновременно оптимальным для любой подгруппы исходных скважин [1]. Это позволяет использовать методы динамического программирования для нахождения оптимального решения, последовательно оптимизируя работу подгрупп все более расширяющегося состава [5, 9]. При этом осуществляется оптимизированный перебор возможных вариантов дебитов газа, для чего ряд возможных дебитов газа должен быть дискретизирован. Подобное решение было использовано в [6, 10] и показало высокую скорость расчета. Однако при некоторых дополнительных допущениях на вид целевой функции возможно существенное упрощение способа решения задачи (7).
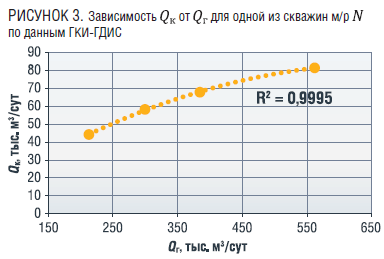Прежде всего, можно заметить, что зависимости получаемые при проведении ГКИ-ГДИС, всегда имеют вид монотонно возрастающих функций, выпуклых вверх. На рисунке 3 показан характерный вид результатов исследований одной из скважин месторождения N. На рисунке 3 приведен также график квадратичной регрессионной кривой, построенной по точкам. Коэффициент корреляции для регрессионной кривой равен 0,9995, что говорит о достаточности использования регрессионных зависимостей второго порядка.
Аналогичное поведение демонстрируют зависимости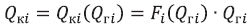 
в (5), получаемые в явном виде при исключении давления. В таком случае их можно заменить регрессионными аппроксимациями квадратичного вида
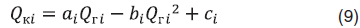
Задача оптимизации тогда превращается в задачу квадратичной оптимизации [4]
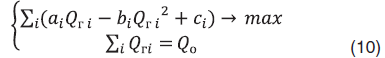
Задача квадратичной оптимизации может быть решена аналитически для подгруппы из двух скважин. При этом сразу возникает вопрос о возможности нахождения оптимального решения для всей группы при известных точных решениях для всех пар. Можно заметить, что в общем случае основным препятствием выступает явная зависимость оптимальных дебитов скважин внутри пары от их суммарного, т.е целевого дебита. Т.к. оптимальные целевые дебиты пар в глобальном (для группы n-скважин) оптимальном решении изначально неизвестны, то напрямую воспользоваться парными решениями в общем случае нельзя. В работе [1] была рассмотрена задача квадратичной оптимизации двух скважин вида
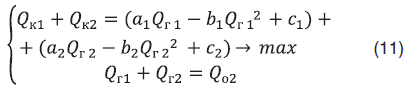
Полученное оптимальное решение (11) имеет вид
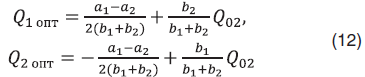
Как следует из (12), оптимальные решения ожидаемо зависят от целевого дебита , что на первый взгляд не позволяет воспользоваться ими при решении задачи общей оптимизации. Однако замена переменной
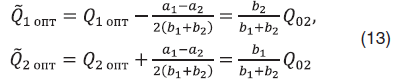
позволяет установить независимое от целевого дебита отношение дебитов скважин внутри пары
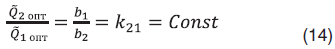
Из (14) можно найти связь дебитов
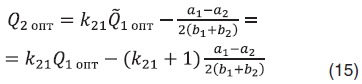
Оптимальное решение в таком виде уже не зависит от целевого дебита пары и связывает с , которую можно принять за независимую переменную. Выражение вида (15) будет справедливым для любой пары скважин. Удобно рассмотреть пары первой скважины со всеми оставшимися и определить тем самым оптимальные дебиты этих скважин в зависимости от единственной переменной . Тогда ограничение по дебиту газа в задаче (10) позволит восстановить значения всех дебитов
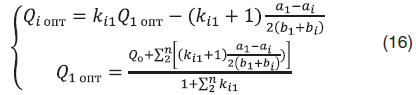
Система (16) дает точное решение задачи оптимизации (10) и представляет собой приближенное решение задачи (3). Точность полученного решения определяется степенью близости точных зависимостей к квадратичной, которая, как было отмечено выше, весьма высока.
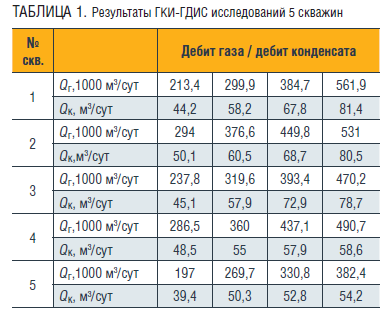
В качестве примера использования предложенной методики расчета оптимальных дебитов газа (16) рассмотрим пример оптимизации ТР работы скважин месторождения N. В таблице 1 приведены результаты исследований 5 скважин
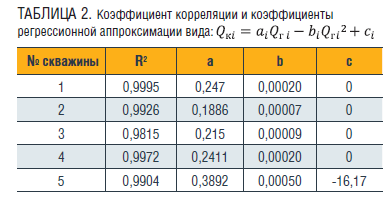В таблице 2 приведены результаты регрессионной аппроксимации данных таблицы 1: коэффициенты корреляции и коэффициенты квадратичных уравнений.
Как видно из таблицы 2, квадратичные регрессии с высокой точностью аппроксимируют экспериментальные данные по всем скважинам. 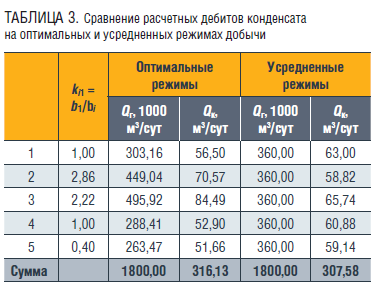В таблице 3 представлены результаты расчета оптимальных дебитов газа и конденсата в сравнении с дебитами на усредненных дебитах газа.
Как следует из таблицы 3, суммарный дебит конденсата от 5 скважин в оптимальном режиме составил 316,13 м3/сут, что на 2,8 % выше дебита, достигнутого на усредненном режиме добычи. Прибавка в добыче конденсата зависит от величины целевого дебита по газу и может достигать 4–5 % в сравнении с усредненными режимами при суммарном целевом дебите газа 2000–2100 тыс. м3/сут. При этом наибольший дебит вполне ожидаемо получают скважины с большим значением коэффициента .
Полученные аналитическим методом оптимальные решения позволяют полностью восстановить недостающие параметры ТР всей ГСС с помощью специализированного ПО (например, Pipesim, GAP и пр.). Для этого достаточно задать значения оптимизированных дебитов газа и состав газа для каждой скважины в соответствии с забойным давлением, которое можно определить исходя из уравнения (1).
Заключение
В статье рассмотрены подходы к расчету оптимальных краткосрочных режимов работы добывающих скважин газоконденсатного месторождения, максимизирующие добычу конденсата. Предложено использовать прямую зависимость дебита конденсата от дебита газа, получаемую при проведении ГКИ. Показано, что вид этой зависимости позволяет использовать квадратичную аппроксимацию, допускающую точное аналитическое решение задачи минимизации пластовых потерь. Получены точные аналитические выражения для вычисления оптимальных дебитов. Рассмотренные примеры анализа результатов реальных промысловых экспериментов показали возможное увеличение добычи конденсата на 2–5 % по сравнению с добычей на усредненных режимах. Предложенный подход позволяет построить универсальный алгоритм краткосрочной оптимизации добычи конденсата. При переходе к задачам долгосрочной оптимизации потребуется учитывать как взаимное влияние скважин друг на друга, так и эффекты постепенного выпадения конденсата в пласте за счет снижения пластового давления в ходе добычи.
Литература
1. Вершинин В.Е., Коваленко А.П., Женыспаев Д. С., Ковалькова А.С., Выдренков А.Д. Оптимизация отборов газа добывающих скважин для повышения эффективности добычи конденсата // Вестник Тюменского государственного университета, Физико-математическое моделирование. Нефть, газ, энергетика. Том 9. № 4 (36). С. 128–142.
2. Гриценко А.И., Алиев З.С., Ермилов О.М., Ремизов В.В., Зотов Г.А. 1995. Руководство по исследованию скважин. М.: Наука. 523 с.
3. Дурмишьян А.Г. 1979. Газоконденсатные месторождения. М.: Недра. 335 с.
4. Зангвилл У.И. 1973. Нелинейное программирование. Единый подход. М.: Советское радио. 312 с.
5. Левитин А.В. Алгоритмы: введение в разработку и анализ: Пер. с англ.–М.: Издательский дом «Вильямс», 2006, 576 с.
6. Рязанцев А.Э., Торопецкий К.В., Платонов Ю.Г., Вершинин В.Е., Григорьев А.В., Черемисин А.Н., Ульянов В.Н., Курмангалиев Р.З., Колотилов В.А. 2015. Моделирование технологических режимов работы газоконденсатных скважин // Вестник ЦКР Роснедра. № 2. С. 20–27.
7. Трубачева И.А., Ермолаев А.И., Некрасов А.А. 2018. Метод распределения заданного отбора газа по скважинам газоконденсатного месторождения с целью увеличения конденсатоотдачи // Автоматизация, телемеханизация и связь в нефтяной промышленности. № 3. С. 35–40. https://doi.org/10.30713/0132-2222-2018-3-35-40.
8. Чарный И.А. 1963. Подземная гидрогазодинамика. М.: Гостоптехиздат. 396 с.
9. Grigoryev A. V., Vershinin V. E. 2014. Universal optimization algorithm for gas-condensate gathering // Asian Journal of Applied Sciences. Vol. 2. No. 6. Pp. 912–915.
10. Vershinin V. E., Grigoryev A. V., Fedorov K. M. 2016. Problems of gas condensate field production solved by novel enlarged block simulator // SPE Russian Petroleum Technology Conference and Exhibition (24–26 October 2016, Moscow, Russia). Paper SPE-182053-MS. https://doi.org/10.2118/182053-MS.
