На современном этапе по оценкам, приведенным в [1], системы на основе электропривода потребляют больше 60 % производимой в мире электроэнергии. Отсюда следует, что оптимизация энергопотребления в целом напрямую зависит от эффективности использования возможностей электродвигателей. С одной стороны такая оптимизация необходима с точки зрения сокращения потребления невозобновимых минеральных ресурсов для производства электроэнергии и сопутствующих этому процессу вредных выбросов в окружающую среду. С другой стороны построение энергооптимального электропривода необходимо в случае проектирование систем специального назначения.
К последним системам можно отнести и разрабатываемые в настоящее время необслуживаемые циклоидальные электроприводы с энергоаккумулятором, предназначенные для применения с запорной и запорно-регулирующей арматурой на объектах магистральных газопроводов, распределительных газопроводов, газозаправочных станциях, объектах добычи и подготовки газа. Естественно, что к данному типу электроприводов предъявляются жесткие требования по надежности, безопасности, качеству регулирования, скорости срабатывания и многим другим критериям. Однако одним из главных предъявляемых требований является возможность продолжительной автономной работы для обеспечения перестановок рабочего органа при исчезновении электроснабжения на период до нескольких суток. При этом электропривод должен работать от собственного энергоаккумулятора соизмеримой мощности без возможности его подзарядки.
Рассмотрим возможность оптимизации энергоэффективности электропривода, построенного на базе асинхронного двигателя (АД) с векторным управлением. Здесь стоит отметить, что наибольшего КПД (от 80 до 95 %), то есть отношения потребляемой мощности к полезной мощности на валу, можно добиться при работе на номинальную нагрузку. Однако в большинстве режимов АД работает со значением нагрузки менее 75 % от номинала, что приводит к значительному снижению энергоэффективности и росту магнитных и электрических потерь.
В существующей литературе предлагается несколько подходов улучшения энергоэффективности АД за счет сокращения потерь в приводе. Все эти подходы можно разделить на три большие группы: методы оптимизации потокосцепления ротора при минимизации потребляемой мощности (в англоязычной литературе [2], [3], [4] используется термин Search Control), методы оптимизации потокосцепления ротора на основании модели потерь АД (в англоязычной литературе [5] используется термин Loss-Model-Based Control), методы, использующие комбинацию первых двух [6].
Идея первой группы методов состоит в минимизации потребляемой мощности для заданного момента нагрузки и частоты вращения ротора АД за счет изменения сигнала задания потокосцепления ротора. Основными достоинствами данного метода является его малая чувствительность к вариациям параметров АД, а также возможность построения системы управления без априорной информации о значениях активных и индуктивных сопротивлений обмоток статора и ротора. Однако у данного метода есть и недостатки: время поиска оптимального значения потокосцепления ротора может быть довольно существенным. Также может потребоваться перезапуск алгоритма поиска в случае возникновения колебаний вокруг точки оптимума. В настоящее время при проектировании систем управления с использованием данных методов широкое применение находят интеллектуальные методы оптимизации на базе нечеткой логики и нейронечеткого подхода.
Вторая группа методов позволяет формализовать поиск точки оптимума. Для этого используются математические методы, которые опираются на модель АД и график зависимости потокосцепления ротора от тока статора, полученную экспериментальным путем. Данный метод позволяет аналитически определить оптимальное значение потокосцепления ротора, однако чувствителен к вариации параметров АД.
Рассмотрим пример построения энергооптимального автоматизированного электропривода на базе АД на примере системы с векторным управлением при ориентации по потокосцеплению ротора, функциональная схема которого приведена на рисунке 1.
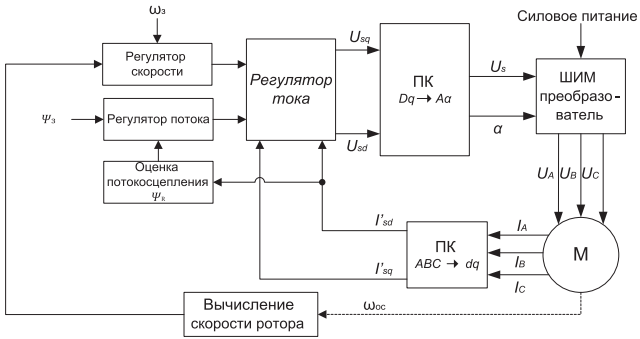
Рисунок 1. Система векторного управления АД
В рамках статьи мы опустим описание работы приведенной схемы, его можно найти в материалах Соколовского Г.Г. [7]. Важно, что обычно значение потокосцепления ротора задается равным номинальному значению. Однако это не всегда обеспечивает оптимальную энергоэффективность. Поэтому предлагается несколько модифицировать традиционную схему векторного управления к виду, приведенному на рисунке 2 и 3.
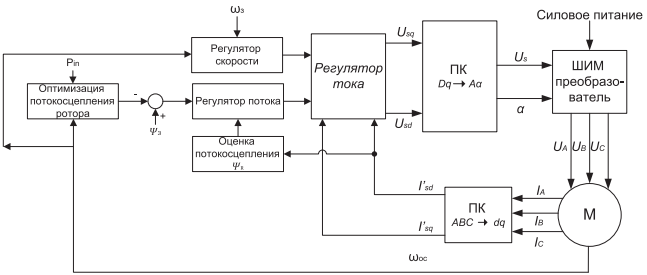
Рисунок 2. Система векторного энергооптимального управления АД при оптимизации по минимуму потребляемой мощности
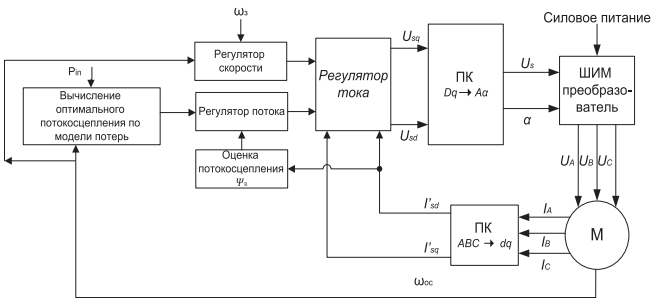
Рисунок 2. Система векторного энергооптимального управления АД при оптимизации по модели потерь
Подробнее рассмотрим методы оптимизации потокосцепления ротора. В первую группу входят методы минимизации мощности, потребляемой системой. В рамках данной группы методов поиск минимума потребляемой мощности производится в установившемся режиме с помощью различных алгоритмов оптимизации. Так в [8] предлагается использовать алгоритм безусловной оптимизации Розенброка.
Рассмотрим наиболее простой для реализации алгоритм данной группы методов, приведенный в дискретной форме. Изначально происходит расчет потребляемой мощности по показаниям датчиков в звене постоянного тока согласно (1)
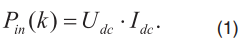
После того, как значение потребляемой мощности установится, начинается процесс оптимизации потокосцепления ротора. При этом если значение частоты вращения ротора отклоняется от заданного, то процесс оптимизации начинается сначала. Сам процесс оптимизации представляет собой изменение сигнала задания потокосцепления ротора с малым шагом и оценка потребляемой мощности для каждого значения потокосцепления ротора. В случае если каждое следующее значение потребляемой мощности уменьшается, то потокосцепление увеличивается с определенным шагом. В противном случае значение потокосцепления увеличивается, но с меньшим, чем ранее, шагом. Математически алгоритм описывается формулами с (2) по (4).
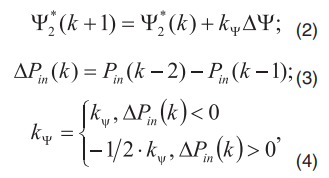
где
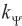
- переменная составляющая приращения потокосцепления ротора;
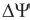
- начальный шаг приращения потокосцепления ротора.
В результате выполнения приведенного алгоритма достигается оптимальное значение потокосцепления ротора. Однако сам процесс приведенной оптимизации относительно долог, поэтому результаты его работы можно использовать в качестве обучающей выборки для нейронечеткой сети, которую в дальнейшем можно использовать в качестве регулятора потокосцепления ротора.
Вторая группа методов, как говорилось ранее, опирается на модель АД.
Для объяснения одного из алгоритмов, позволяющих взамен потерь мощности минимизировать ток статора при заданном напряжении статора, необходимо показать некоторые соотношения между переменными АД, приведенные в [3], [4] в относительных единицах.
Введем нормированную частоту поля статора
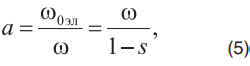
где

- частота электрического поля статора;

- частота вращения ротора;
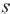
- скольжение АД.
Токи намагничивания и ротора определяются соответственно следующими выражениями
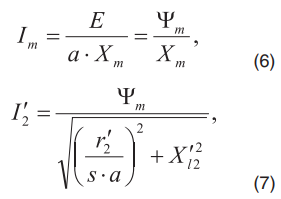
где
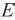
- ЭДС взаимоиндукции;
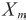
- индуктивное сопротивление взаимоиндукции;
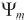
- потокосцепление в воздушном зазоре;

- сопротивление рассеяния ротора;
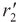
- активное сопротивление ротора.
Выражение (7) можно переписать относительно потокосцепления в воздушном зазоре (главного потокосцепления)
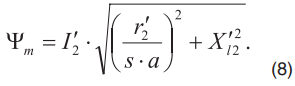
Электромагнитный момент рассчитывается согласно (9)

Тогда, подставив (7) в (9) можно получить следующее

Учитывая, что АД обычно работает в режимах с малыми значениями скольжения можно предположить, что 
В этом случае можно переписать выражения (8) и (10) следующим образом

Следуя [3], запишем, что

Где
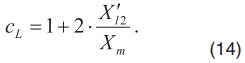
Кроме того, в приведенном алгоритме, как говорилось ранее, используется кривая намагничивания, снятая экспериментально и аппроксимированная полиномом пятой степени

где
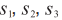
- коэффициенты, полученные при аппроксимации экспериментально полученных точек кривой намагничивания.
На основании выражений (13), (12) и (15) можно переписать выражение для тока статора как
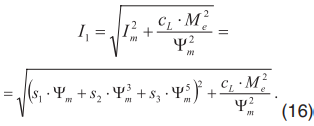
Таким образом, получена зависимость тока статора от потокосцепления в воздушном зазоре. Исследуя выражение (16) на экстремумы, можно вычислить оптимальное значение потокосцепления, необходимое для минимизации тока статора. При этом в [3] показано, что минимизация тока статора дает результат, близкий к минимизации потребляемой мощности.
Другой вариант алгоритма из второй группы методов приведен в [5]. Там предлагается записать суммарную мощность потерь в следующем виде
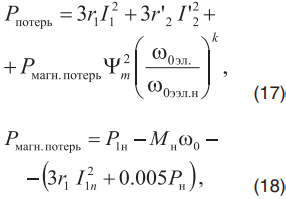
где

- номинальная частота питающей сети;
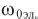
- частота питающей сети;

- номинальная потребляемая мощность;
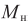
- номинальный момент;
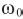
- синхронная частота вращения ротора АД;

- добавочные потери,
k – коэффициент, характеризующий свойства металла сердечника.
В [5] показано, что соотношение (13) с учетом допущений можно переписать как
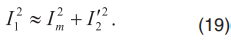
Кроме того, ток ротора может быть представлен как
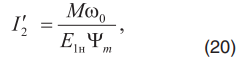
а ток намагничивания
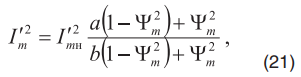
где
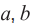
- коэффициенты аналитической аппроксимации кривой намагничивания.
Тогда, используя выражения с (17) по (21), можно показать, что

Далее можно произвести аналитическое исследование функции мощности потерь, задаваемой выражением (22), на наличие экстремумов. В результате нахождения производной и приравнивания ее к нулю получим уравнение восьмой степени
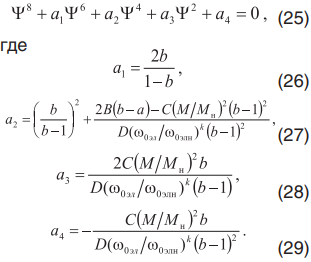
Очевидно, что уравнение (25) имеет восемь корней. Однако при решении этого уравнения в результате получаются 6 комплексных корней, один действительный отрицательный и один действительный положительный. Так как решением является модуль потокосцепления, то комплексные корни и отрицательный не имеет физического смысла. Таким образом, получено значение потокосцепления, обеспечивающее минимальное значение мощности потерь.
В работе [6] приведен анализ эффективности двух описанных здесь групп методов на примере системы векторного управление АД мощностью 550 Вт. Здесь приведем результаты моделирования, выполненного в САПР Matlab в работе [6] на рисунках 5 и 6. При этом на рисунке 4 показано изменение задания по скорости и нагрузки на АД.
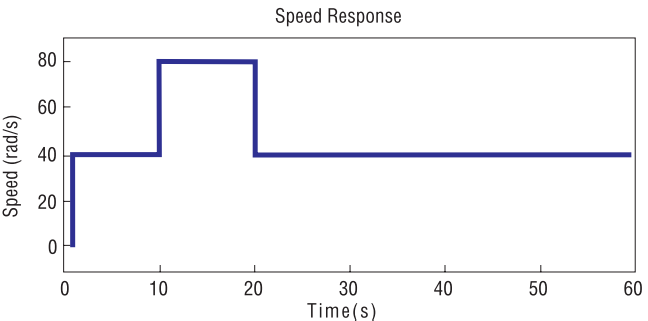

Рисунок 4. Сигнал задания скорости и момента нагрузки АД
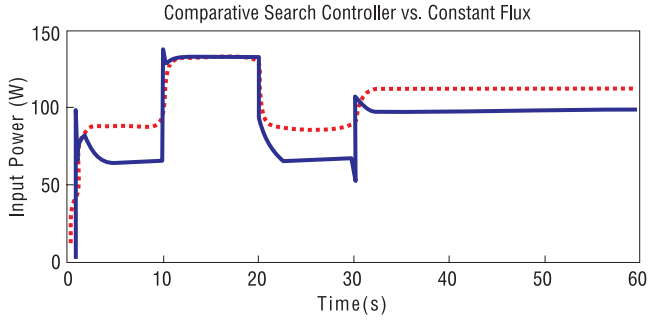
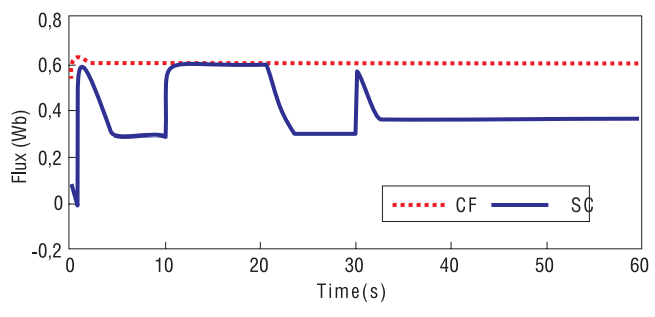
Рисунок 5. Результат сравнительного моделирования работы схемы при постоянстве потокосцепления ротора и при оптимизированном без модели потерь потокосцеплении
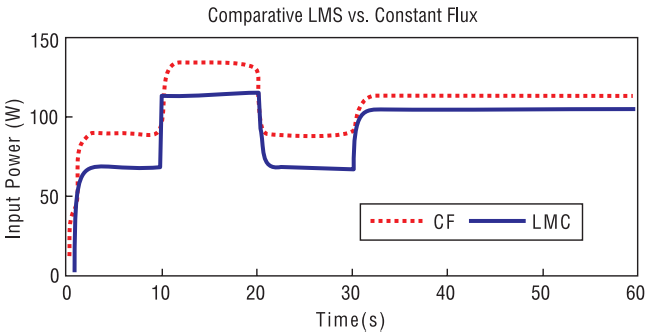
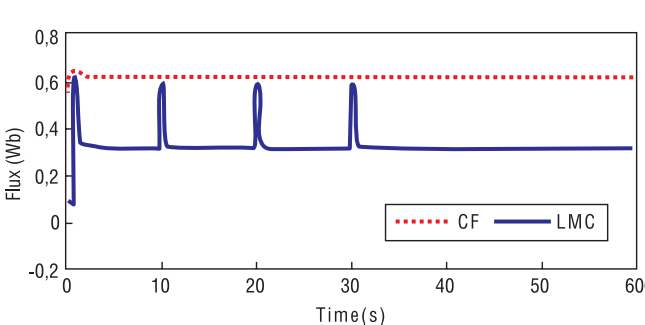
Рисунок 6. Результат сравнительного моделирования работы схемы при постоянстве потокосцепления ротора и при оптимизированном по модели потерь потокосцеплении
В результате проведенных исследований можно сделать вывод, что обе системы дают значительное уменьшение потребляемой мощности при сохранении заданных динамических характеристик системы.
Одним из вариантов создания необслуживаемого циклоидального электропривода с энергоаккумулятором может стать комбинирование двух приведенных методов с учетом достоинств и недостатков каждого из них, и возможностью адаптации второго метода к вариации параметров АД.
Список литературы
1. Тунбаев И., Павлов С. В,., Тенденции развития автоматизированного электропривода в нефтегазовой отрасли. Вестник Алматинского университета энергетики и связи № 3/2 (10), 2010, с. 19-23, 136
2. Thanga Raj, S. P. Srivastava, P. Agarwal. Energy Efficient Control of Three-Phase Induction Motor – A Review. International Journal of computer and Electrical Engineering. vol. 1, pp. 61-70, April 2009
3. I. Kioskeridis, N. Margaris. Loss minimization in scalar-controlled induction motor drives with search controllers. IEEE Transactions on Power Electronics, vol. 11, № 2, pp. 213-220, March 1996
4. I. Kioskeridis, N. Margaris. Loss minimization in induction motor adjustable-speed drives. IEEE Transactions on Industrial Electronics, vol. 43, № 1, pp. 226-231, February 1996
5. R. AL-Issa, H. Sarhan. Modeling and simulation of flux-optimized induction motor drive. Research Journal of Applied Sciences, Engineering and Technology, vol. 2, pp. 603-613. September 2010
6. Scarmin, A., Gnoatto, C.L., Aguiar, E.L.. Hybrid Adaptive Efficiency Control technique for energy optimization in induction motor drives. Industry Applications (INDUSCON), 2010 9th IEEE/IAS International Conference. 8-10 Nov. 2010. pp. 1-6
7. Соколовский Г.Г. Электроприводы переменного тока с частотным регулированием. –М.: ACADEMA, 2006. – 265 с.
8. D. A. Souza, W. C. P. Aragao Filho, G. C. D. Sousa. Adaptive Fuzzy Controller for Efficiency Optimization of Induction Motors. IEEE Transactions on Industrial Electronics Vol.54 , Issue: 4 pp. 2157 – 2164, Aug. 2007






