Одной из задач газотранспортной системы при сезонной и суточной неравномерности потребления природного газа является согласование объемов потребления газа с пропускной способностью газопровода при обеспечении оптимальной загрузки газоперекачивающего оборудования. Пропускная способность магистрального газопровода нелинейно зависит от большого числа параметров, таких как степень повышения давления в газоперекачивающих агрегатах (ГПА), давление и температура транспортируемого газа и его теплофизические свойства, протяженность и диаметр трубопровода и др. Для решения эксплуатационных задач, связанных с изменением режима работы МГ, необходимо знать, как влияют изменения параметров МГ и характеристик ГПА на условиях их совместной работы, на пропускную способность МГ, потребляемую мощность и КПД газоперекачивающих агрегатов. Для этого авторами предложено использовать метод малых отклонений [1], который позволит подойти к решению системы линейных алгебраических уравнений и достаточно просто получить требуемые результаты в общем и численном виде, удобном для анализа и практического использования.
Влияние параметров газотранспортной системы на её производительность установим, используя уравнение для определения коммерческой производительности на участке МГ [2]:

где:
D – диаметр газопровода;
LКЦ – длина линейного участка газопровода между компрессорными цехами;
Т – осредненная температура на участке газопровода;
РН, РК – давление в начале и в конце участка газопровода соответственно;

Зависимость коммерческой производительности Q линеаризуется при условии, что все параметры, включенные в уравнение (1), являются взаимно независимыми переменными.
Для этого прологарифмируем и продифференцируем уравнение (1), имея ввиду, что
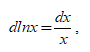
и при допущении неизменности теплофизических свойств природного газа получим:
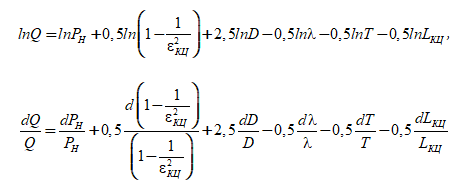
Преобразуем дифференциал:
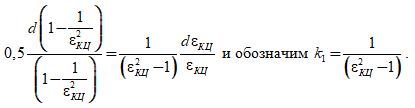
Затем все дифференциалы dx заменим приращением Δx, а относительное приращение

обозначим δx.
Уравнение (1) преобразуется к линеаризованному виду:

Для расчета коэффициента гидравлического сопротивления отраслевыми нормами проектирования [3] рекомендуется зависимость:

где: Re – число Рейнольдса; КЭ – относительная шероховатость; Е – коэффициент эксплуатационной эффективности трубопровода; λтр – гидравлические потери на трение.
В магистральных газопроводах наиболее распространено течение газа в квадратичной зоне турбулентного режима при
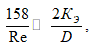
получаем частный случай для коэффициента гидравлических потерь МГ:

Линеаризуем данное уравнение в соответствии с указаниями [1]:
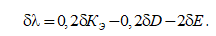
Относительное изменение коэффициента гидравлических потерь подставляем в уравнение относительного изменения коммерческой производительности и получаем его окончательный вид:

Данное уравнение устанавливает линейную зависимость δQ от относительного изменения давления в начале участка МГ δРН, диаметра трубопровода δD, изменения коэффициентов относительной шероховатости δКЭ, гидравлических потерь δλ, эксплуатационной эффективности δЕ, температуры δТ, длины участка δLКЦ и степени повышения давления на КЦ δɛКЦ. Из полученного уравнения можно сделать следующее заключение: коэффициенты, стоящие перед δКЭ, δLКЦ, δD, и δТ, величины постоянные, не зависящие от начальных значений параметров трубопроводной системы. Знак плюс перед коэффициентами устанавливает прямо пропорциональное влияние относительного изменения параметра на итоговую величину, минус соответственно обратно пропорциональное влияние, то есть при увеличении температуры газа на 1 % производительность участка МГ снизится на 0,5 %. В данном уравнении только величина коэффициента k1 однозначно определяется исходным (проектным) значением степени повышения давления εКЦ в компрессорном цеху. Проанализируем характер влияния относительного изменения степени повышения давления εКЦ на пропускную способность участка газопровода. Линеаризованное уравнение производительности участка МГ при условии, что входящие в него величины, кроме δεКЦ, неизменны, принимает вид:
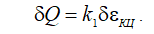
Для различных значений начальной степени повышения давления εКЦ представлена графическая зависимость изменения коэффициента влияния k1.
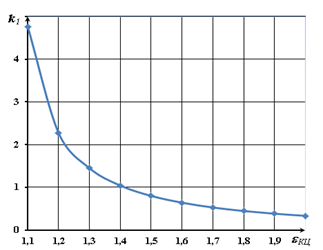
РИС. 1. Зависимость коэффициента k1 от проектной величины εКЦ
Из графической зависимости видно: чем больше проектное значение εКЦ, тем меньше значение коэффициента влияния k1. Для двух значений степени повышения давления εКЦ = 1,35 и εКЦ = 1,44 построена на рис. 2 графическая зависимость δQ = f (δεКЦ) с шагом относительного изменение δεКЦ = 5 %.
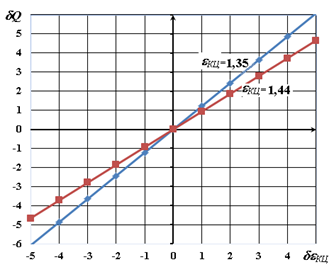
РИС. 2. Графическая зависимость δQ = f (δεКЦ)
При степени повышения давления εКЦ = 1,44 снижение ее на 1 % приведет к снижению производительности участка МГ на 0,93 %, а при степени εКЦ = 1,35 снижение производительности составит 1,22 %. Следовательно, при небольших значениях проектной εКЦ для согласования объемов потребления газа с производительностью центробежного нагнетателя (ЦН) необходимо незначительное изменение режимов работы ЦН и приводного газотурбинного двигателя. При отклонениях от номинального режима работы ГПА, соответствующего наибольшему КПД, снижение мощности приводит к увеличению расхода топливного газа и снижению политропического КПД нагнетателя, а увеличение мощности дополнительно приводит к быстрому износу оборудования. Для успешного использования данного метода необходимо ясно представлять его возможности и пределы применимости. Метод дает хорошую точность только при относительном изменении параметра в пределах ±5 %, а при больших отклонениях может привести к большим погрешностям. Достоинство метода заключается в его простоте, хотя он и связан с большим числом вычислений. Метод малых отклонений можно применить и к анализу производительности магистрального газопровода с n-числом компрессорных цехов при проектной разработке газотранспортной системы, с учетом технических возможностей оборудования и протяженности участков.
Литература
1. Черкез А.Я. Инженерные расчеты газотурбинных двигателей методом малых отклонений. / Издательство: М.: Машиностроение: 1975 / 3-изд. пер. и доп. С. 380.
2. Теория трубопроводного транспорта газа: учебное пособие / С.А. Гулина, А.С. Гулина. – Самара: Самар. гос. техн. ун-т, 2019. – 140 с.
3. ГОСТ 30319.2-96. Газ природный. Методы расчёта физических свойств.
Keywords: main gas pipeline, method of small deviations, influence coefficients.






