Практика показывает, что надземные участки трубопроводов в определенных условиях могут подвергаться интенсивным колебаниям. Если амплитуды этих колебаний превышают предельные значения, это может привести к разрушению объекта. Для обеспечения безопасности и повышения эффективности работы необходимо проводить расчеты вибрационных характеристик надземных трубопроводов в соответствии с требованиями, изложенными в [1]. Чтобы оценить устойчивость трубопроводов к вибрациям и найти наиболее эффективные методы предотвращения резонансных колебаний, необходимо определить собственные частоты колебаний и характеристики колебательных процессов.
Исследованиям влияния внутреннего давления и скорости перекачиваемой жидкости посвящены работы [2–12]. В работе [13] получена математическая модель для определения частот свободных колебаний надземных участков трубопроводов, транспортирующих несжимаемую жидкость.
Для анализа колебаний трубопровода его можно представить в виде прямого стержня, для описания поперечных деформаций стержня при воздействии продольных усилий используется соответствующее дифференциальное уравнение поперечных деформаций стержня при воздействии продольных усилий [14]:
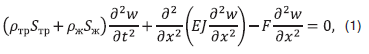
где – плотности материала трубопровода и перекачиваемой жидкости,
– площади сечения трубопровода и жидкости, E – модуль упругости материала трубопровода, J – момент инерции сечения трубопровода, F – растягивающие усилия, w – смещение оси трубопровода в поперечном направлении.
Растягивающее усилие может быть представлено в виде суммы составляющих:
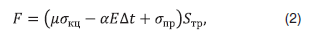
где μ – коэффициент Пуассона материала трубы, α – коэффициент линейного расширения материалы трубы, ∆t – температурный перепад, – дополнительные напряжения в продольном направлении, – кольцевые напряжения, возникающие в стенках трубопровода, определяются как: Pxdвн/2δ, Рx – давление, dвн – внутренний диаметр трубопровода, δ – толщина стенки трубопровода.
При подстановке (2) в (1) и пренебрегая температурным расширением и дополнительной деформацией в продольном направлении, получим уравнение, описывающее колебания трубопровода с учетом внутреннего давления, которое будет иметь вид:
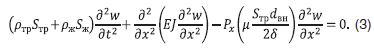
Скорость перекачиваемой несжимаемой жидкости характеризует снижение начального давления по длине трубопровода и учитывается при расчете градиента давления при расчете давления в каждой точке сечения – Px.
Так, уравнение (3) вместе с граничными условиями представляет собой математическую модель для определения частот свободных колебаний надземных трубопроводов, транспортирующих несжимаемую жидкость. Решение может быть получено с помощью численного метода Бубнова-Галеркина [13].
Полученная математическая модель позволяет оценить влияние характеристик перекачиваемой жидкости (плотности – ρж и давления – Px) для надземного участка с характеристиками: диаметр – 219 мм., толщина стенки – 7 мм., длина пролета – 9,9 м. Результаты оценки представлены на рисунках 1 и 2.
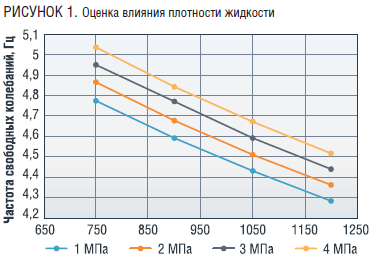
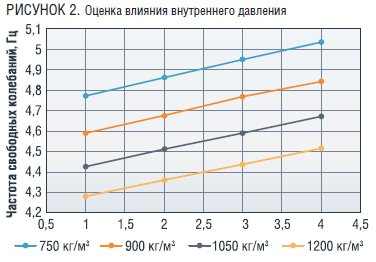
Анализ результатов показал, что при увеличении плотности перекачиваемой жидкости частота свободных колебаний снижается, так как увеличивается общая масса системы. При увеличении внутреннего давления, наоборот, частота свободных колебаний возрастает, поскольку увеличивается жесткость системы. Таким образом, увеличение давления при увеличении плотности перекачиваемой жидкости может скомпенсировать изменение частоты свободных колебаний, и она останется в том же диапазоне значений.
Авторы выражают признательность за поддержку Национальному проекту «Наука и университеты» Министерства науки и высшего образования Российской Федерации, грант № FEWN-2021-0012.
Литература
1. СА 03-003-07. Расчеты на прочность и вибрацию стальных технологических трубопроводов: нормативные документы межотраслевого применения по вопросам промышленной безопасности и охраны недр: дата введения 2006-11-27 / Российская ассоциация экспертных организаций техногенных объектов повышенной опасности. – Изд. официальное. – Москва: Стандартинформ, 2007. – 72 с. – Текст: непосредственный.
2. Феодосьев В.И. О колебаниях и устойчивости трубы при протекании через нее жидкости / В.И. Феодосьев. – Инж. сборник. – 1952. – т. 10. – с. 169–170. – Текст: непосредственный.
3. Ефимов А.А. Свободные колебания подводных нефтепроводов / А.А. Ефимов. – Известия вузов. Нефть и газа. – 2008. – № 1. – с. 49–56. – Текст: непосредственный.
4. Ильин В.П. Исследование свободных колебаний кривой трубы с потоком жидкости / В.П. Ильин, В.Г. Соколов. – Изд. Сарат. ГТУ, «Успехи строительной механики и теории сооружений» / Сб. трудов СГТУ и РААСН. – 2010. – с. 88–93. – Текст: непосредственный.
5. Соколов В.Г. Уравнения движения криволинейного участка трубопровода с потоком жидкости / В.Г. Соколов, А.В. Березнев. – Изв. вузов. Нефть и газ. – 2004. – № 6. – С. 76–80. – Текст: непосредственный.
6. Соколов В.Г. Решение задачи о свободных колебаниях криволинейных участков трубопроводов с протекающей жидкостью / В.Г. Соколов, А.В. Березнев. – Изв. вузов. Нефть и газ. – 2005. – № 1. – С. 80–84. – Текст: непосредственный.
7. Зарипов Д.М. Нелинейные колебания трубопровода под действием внутреннего ударного давления жидкости / Д.М. Зарипов. – Труды Института механики Уфимского научного центра РАН. Вып. 11. Уфа: Гилем. 2016. С. 136–140. – Текст: непосредственный.
8. Миронов М.А. Вынужденные колебания трубы с потоком жидкости / М.А. Миронов, П.А. Пятаков, А.А. Андреев. – Акустический журнал. 2010. Т. 56. № 5. С. 684–692. – Текст: непосредственный.
9. Шакирьянов М.М. Пространственные хаотические колебания трубопровода в сплошной среде под действием переменного внутреннего давления / М.М. Шакирьянов. – Известия Уфимского научного центра РАН. 2016. № 4. С. 35–47. – Текст: непосредственный.
10. Ганиев Р.Ф. Пространственные непериодические колебания трубопровода под действием переменного внутреннего давления / Р.Ф. Ганиев, М.А. Ильгамов, А.Г. Хакимов, М.М. Шакирьянов. – Проблемы машиностроения и надежности машин. 2017. № 2. С. 3–12. – Текст: непосредственный.
11. Черенцов Д.А. Mатематическая модель манометрической пружины в вязкой среде / Д.А. Черенцов, С.П. Пирогов, С.М. Дорофеев. Вестник Тюменского государственного университета. Физико-математическое моделирование. Нефть, газ, энергетика. 2014. № 7. С. 234–241. – Текст: непосредственный.
12. Чуба А.Ю. Определение собственных частот колебаний изогнутых труб некругового поперечного сечения / А.Ю Чуба., Н.И Смолин, С.П.Пирогов. Известия высших учебных заведений. Нефть и газ. 2007. № 1 (61). С. 77–82. – Текст: непосредственный.
13. Черенцов Д.А. Определение частот свободных колебаний надземных участков трубопроводов, транспортирующих несжимаемую жидкость / Д.А. Черенцов, С.П. Пирогов. Известия высших учебных заведений. Нефть и газ. 2023. № 3. С. 84–94. – Текст: непосредственный.
14. Черенцов Д.А. Уравнения математической физики в задачах трубопроводного транспорта нефти и газа: учебное пособие / Д.А. Черенцов, С.П. Пирогов, К.С. Воронин, 2019. – 96 с. – Текст: непосредственный.






