Суть технологии ГРП заключается в закачке в нефтеносный пласт специальной жидкости с целью создания искусственной (техногенной) трещины длиной ~100 м, высотой ~10 м и средним раскрытием ~5-10 мм. В результате создается соединенный со скважиной искусственный канал с большой площадью притока, который имеет высокую (на порядки превышающую пластовую) проницаемость. Это обеспечивает значительное увеличение притока пластового флюида к скважине. Инженерные аспекты технологии рассматриваются, например, в [1].
Используемые в настоящее время математические модели развития трещины ГРП в большинстве своем носят «инженерный» характер: в них используются двумерные постановки, априорно заданные геометрические модели трещин, практически никогда не производится корректный учет геомеханических эффектов и так далее, см., например, [1-3]. Использование таких математических моделей давно стало стандартной и сравнительно успешной инженерной практикой. Однако возможностей таких моделей недостаточно для решения ряда важных задач разработки, связанных с динамикой развития трещин ГРП, в которых требуется использование полных корректных (самосогласованных) пространственно-трехмерных постановок. К таким задачам относятся, например, предсказание геометрии и динамики развития трещин в сложной геомеханической обстановке; анализ процедуры множественного ГРП на горизонтальных стволах, когда возникает необходимость учета интерференции соседних трещин; анализ эффекта «авто-ГРП», связанного с самопроизвольным и нежелательным ростом трещин на нагнетательных скважинах и ряд других.
Физико-математическое описание динамики трещины ГРП в ходе ее развития сводится к решению сложной связанной задачи, включающей в себя следующие системы уравнений:
-
система уравнений пороупругости, описывающая эволюцию напряженно- деформированного состояния среды и полей давления флюида в ней в ходе развития трещины;
-
уравнения течения жидкости в трещине;
-
механические условия развития трещины, определяющие направление ее развития в каждой точке ее фронта;
-
заданные на боковых поверхностях трещины условия согласования между полями давления в трещине и в среде, потоками массы, импульса и энергии, а также кинематические условия, связывающие раскрытие трещины и перемещение точек пласта.
Указанные группы уравнений являются основой программы-симулятора для анализа процесса гидроразрыва пласта в рамках «расширенной» постановки, которая разрабатывается в Федеральном исследовательском центре Институт прикладной математики им. М.В. Келдыша РАН.
Построенная в рамках этих работ математическая модель позволяет корректно описывать согласованное распределение возмущений начального поля напряжений регионального масштаба с учетом эффектов, связанных с процессами фильтрации при наличии добывающих и нагнетательных скважин, наличия трещины и ее развития с учетом как региональных, так и индуцированных полей напряжений, течения флюида в трещине. Модель пригодна для анализа эффектов самопроизвольного развития трещины ГРП («авто-ГРП») в пространственных масштабах элемента (ячейки) системы заводнения месторождения.
В качестве модели вмещающей среды используется связанная пороупругая модель Био для описания возмущений начального поля напряжений регионального масштаба, вызванных присутствием и развитием трещины и эффектами фильтрации. Все основные соотношения модели получены для неизотермического случая.
Для описания течения флюида в трещине использованы уравнения гидродинамики в приближении смазочного слоя, в том числе с учетом неизотермических эффектов.
При описании процесса развития трещины использованы физически-обоснованные критерии разрушения с учетом комбинированного режима нагружения в окрестности фронта распространяющейся трещины. В отличие от большинства известных работ, используется критерий для пороупругой задачи (а не чисто упругой), который сформулирован в рамках векторного J- интеграла Черепанова-Райса [4].
Группы уравнений модели (пороупругость, течение в трещине) дополняются условиями согласования, выражающими условия непрерывности потоков консервативных величин (потоков массы, энергии) и геометрические соотношения на трещине как геометрическом разрыве полей перемещений и давления в среде.
Представленная выше математическая модель легла в основу разработанной программы-симулятора, позволяющей моделировать динамику трещины гидроразрыва пласта с учетом сложной геомеханической постановки. Основой используемого вычислительного алгоритма является eXtended Finite Elements Method (X-FEM) [5,6]. Метод основан на дополнении стандартного конечно-элементного базиса специальными дополнительными базисными функциями, которые позволят корректно представить в конечномерном решении разрывные на срединной поверхности трещины поля перемещений, напряжений и деформаций. Одним из ключевых компонентов метода X-FEM является способ представления поверхности трещины в конечномерной задаче, который должен обеспечивать удобство вычисления всех необходимых для реализации метода величин (например, матрицы жесткости задачи). В современных вариантах метода для этого чаще всего используется level set method, см. [7].
В настоящей работе для описания геометрии поверхности использовался оригинальный подход, основанный на методе проекции ближайшей точки. Алгоритмы для описания эволюции оператора проекции ближайшей точки рассмотрены в [8]. В контексте задач о моделировании развития трещин он является таким же общим, как и метод поверхностей уровня, однако обладает рядом преимуществ в том случае, когда граничные условия на боковых поверхностях трещины сами по себе определяются решением некоторых уравнений (в нашем случае – уравнения смазочного слоя). Помимо этого, метод проекции ближайшей точки в настоящее время является удобным средством построения вычислительных алгоритмов для решения уравнений на поверхностях произвольной формы см., [9]. Таким образом, в настоящей работе метод представления ПБТ используется как для представления поверхности в X-FEM, так и для решения уравнения смазочного слоя в трещине. Описание подхода X-FEM/CP представлено в [10].
Примеры работы разработанного программного комплекса для решения ряда различных задач динамики трещины ГРП приведены на рисунках 1-3.
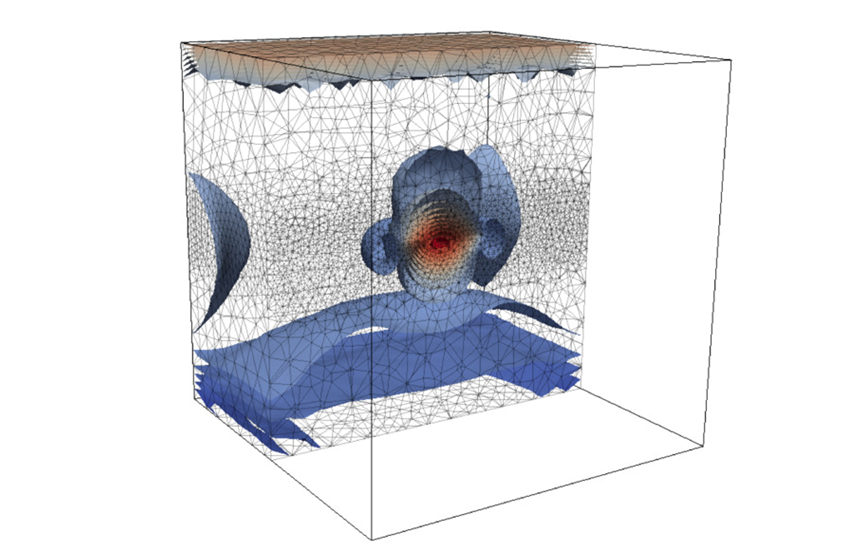
Рис. 1. Изолинии поля давления в окрестности дискообразной трещины
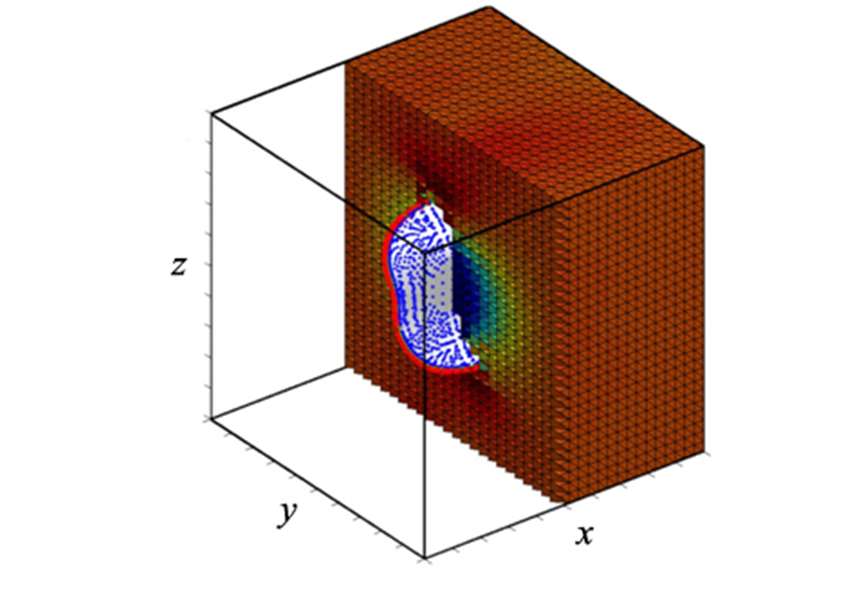
Рис. 2. Распределение напряжений в окрестности эволюционирующей трещины
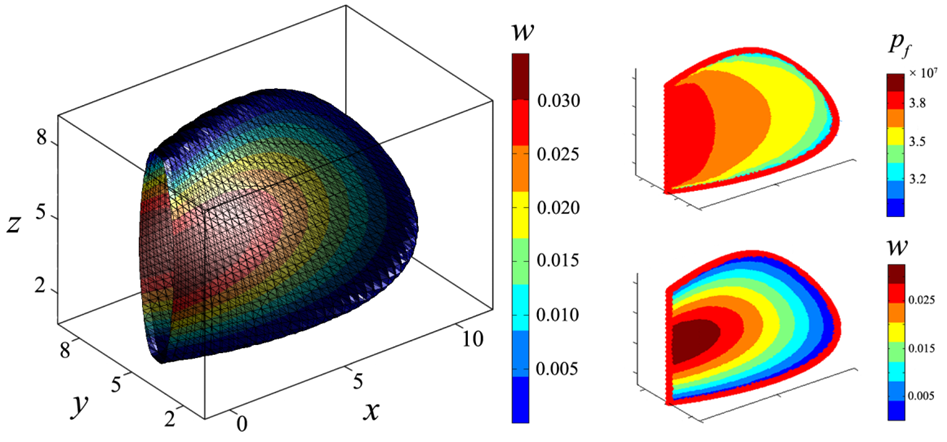
Рис. 3. Распределение раскрытия трещины и давления на ее срединной поверхности
Список литературы
-
Салимов В.Г., Ибрагимов Н.Г., Насыбуллин А.В., Салимов О.В. Гидравлический разрыв карбонатных пластов. – М.: Нефтяное хозяйство, 2013. – 471 c.
-
Экономидес М., Олини Р., Валько П. Унифицированный дизайн гидроразрыва пласта. От теории к практике. – М.: Институт компьютерных исследований, 2007. – 236 c.
-
Michael J. Economides, Kenneth G. Nolte (Eds.) Reservoir Stimulation. Wiley; 3 edition, 2000, – 856 p.
-
Ramazanov M M, Kritsky B V, Savenkov E B 2018 Formulation of J-integral for Biot poroelastic medium Journal of Engineering Physics and Thermophysics 91 6 (accepted)
-
Belytschko T and Black T 1999 Elastic crack growth in finite elements with minimal remeshing Internat. J. Numer. Methods Engrg. 45 601–20
-
Moës N, Dolbow J and Belytschko T 1999 A finite element method for crack growth without remeshing Internat. J. Numer. Methods Engrg. 46 131–50
-
Stolarska M, Chopp D, Moës N and Belytschko T 2001 Modelling crack growth by level sets in the extended finite element method Int. J. Numer. Meth. Engng. 51 943–60
-
Ivanov A V and Savenkov E B 2017 Simulation and visualization of the dynamics of a surface with a movable boundary on a stationary unstructured mesh Scientific Visualization 9 2 64–81
-
Macdonald C B and Ruuth S J 2009 The implicit Closest Point Method for the numerical solution of partial differential equations on surfaces SIAM J. Sci. Comput. 31 4330–50
- Savenkov E B, Borisov V E and Kritsky B V 2018 Utilization of closest point projection surface representation in extended finite element method Mathematical Models and Computer Simulations (accepted)






