Надежность и эффективность трубопроводного транспорта природного газа напрямую зависит от принятия и реализации эксплуатационным персоналом правильных и своевременных решений режимно-технологических задач.
Если в основе правильности решения лежит адекватность методов определения физических и термодинамических свойств природного газа, то в своевременности решений – быстродействие.
Существующие методы определения свойств природного газа по данным о компонентном составе позволяют обеспечить адекватность. Но в основе этих методов лежат уравнения состояния итерационного решения, что негативно сказывается на быстродействии, особенно при обработке в реальном времени больших массивов данных режимно-технологической информации.
Также необходимо отметить, что на текущий момент в газовой промышленности наиболее распространен подход метрологического контроля с использованием данных о неполном компонентном составе природного газа (плотности при стандартных условиях и содержании азота и диоксида углерода).
Отсутствие исходных данных не позволяет использовать методы определения свойств природного газа по данным о компонентном составе, а существующие нормативные уравнения состояния по данным о неполном компонентном составе не позволяют сформировать адекватные методы определения свойств природного газа.
Данная проблема была раскрыта авторами статьи в публикации [7], решение которой сводится к двум возможным направлениям реализации в виде разработки:
-
метода разложения неполного компонентного состава природного газа на эквивалентный компонентный состав (предложенного в [7]), который снимает проблему адекватности, но усугубляет проблему быстродействия,
- метода определения физических и термодинамических свойств природного газа по данным о неполном компонентном составе природного газа.
Разработка метода определения свойств природного газа базируется на использовании подходов термодинамического подобия. Поэтому авторами статьи было проведено вычислительное исследование пределов возможного применения закона соответственных состояний для природного газа.
Было определено, что для обеспечения взаимного отклонения термодинамических функций, в соответствии с требованиями межгосударственного стандарта [2], в пределах 0,2 % – отклонение по плотности при стандартных условиях должно находиться в пределах ± 0,02 кг∙м-3, по содержанию молярных долей азота ± 0,01 и диоксида углерода ± 0,005.
Исходя из этого, нетрудно сделать вывод, что для адекватного определения термодинамических функций природного газа недостаточно одного уравнения состояния с постоянными коэффициентами. Необходима дискретная система уравнений или одно уравнение, но с коэффициентами, изменяемыми в зависимости от неполного компонентного состава природного газа.
В данной статье предложен новый расчетный метод определения физических и термодинамических свойств природного газа по данным о неполном компонентном составе на основе без итерационного уравнения состояния, что позволит решить проблему адекватности и увеличить быстродействие в компьютерных моделях, расчетах режимов и технологических задачах трубопроводного транспорта газа.
Рабочая область применения расчетных методов определения физических и термодинамических свойств природного газа.
Прежде чем рассматривать расчетные методы определения физических и термодинамических свойств природного газа, необходимо определиться с рабочей областью их применения, учитывая ближайшие перспективы развития газотранспортных технологий.
Одним из параметров состояния характеризующим рабочую область является максимальное рабочее давление газотранспортных систем.
Из приведенных данных в таблице 1 видно, что для моделирования процессов транспорта газа на сухопутных участках необходимы расчетные методы определения физических и термодинамических свойств природного газа, охватывающие диапазон рабочих давлений до 12 МПа, на морских участках – до 30 МПа.
ТАБЛИЦА 1. Максимальное рабочее давление, МПа
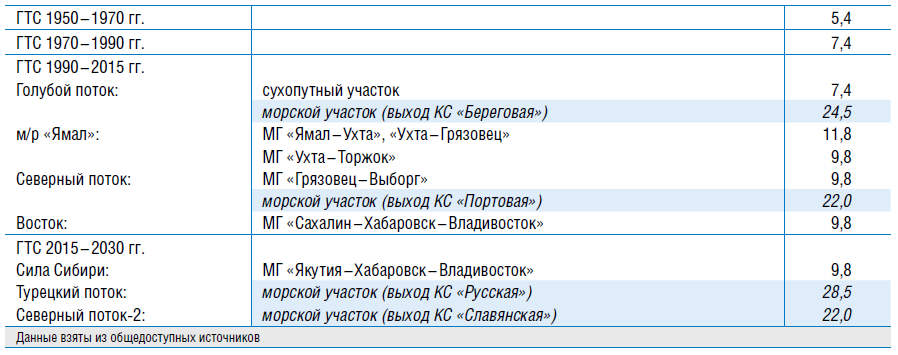
Другим параметром, характеризующим рабочую область, является температура, технологический диапазон которой находится в пределах от 250 до 350 K.
Давление и температура являются параметрами состояния, взаимосвязь которых выражается с помощью уравнения состояния реального газа – природного газа. Поэтому немаловажным фактором в определении физических и термодинамических свойств является сам природный газ. Природный газ – это смесь чистых веществ, состоящая в основном из углеводородных компонентов (алканов), а также неуглеводородных компонентов. Состав природного газа непостоянен, изменяется в зависимости от месторождения природного газа (в том числе по мере выработки месторождения), а также от реализуемых потоковых схем Единой системы газоснабжения Российской Федерации, приводящих к смешению природного газа от разных месторождений в разных пропорциях.
Таким образом, при разработке метода определения физических и термодинамических свойств природного газа были заложены условия применения:
-
по рабочей области давления p £ 12 МПа, температуры 250 £ T £ 350 K;
-
по плотности природного газа при стандартных условиях 0,66819 £ £ 0,73 кг∙м3;
- по молярным долям азота и диоксида углерода £ 0,03; £ 0,01.
Метод определения термодинамических свойств природного газа по данным о плотности при стандартных условиях и содержании азота и диоксида углерода
При разработке уравнения состояния использован следующий вид функциональной зависимости коэффициента сжимаемости:

Псевдокритические параметры природного газа определяются по разработанным авторами формулам

На первом этапе разработки уравнения состояния был сформирован ряд комплексов описания природного газа, дискретно задавая плотность природного газа при стандартных условиях, молярные доли азота и диоксида углерода в пределах условий их применения.

Затем, используя расчетный метод определения термодинамических свойств AGA-8 [5], для каждого компонентного состава в пределах области применения по давлению и температуре был вычислен массив значений функции изотермического отклонения изобарной теплоёмкости от идеально-газового состояния ΔCp и функции отклонения коэффициента сжимаемости (z-1) .
На завершающем этапе по значениям массива этих двух термодинамически связанных функций, применяя последовательную аппроксимацию по приведенному давлению, температуре и параметрам стандартного комплекса описания природного газа, было получено уравнение состояния (3).

Xk – ряд аргументов, полученных из стандартного комплекса описания природного газа с целью упрощения записи формул и алгоритмической части разрабатываемого метода:
|
X0=1, |
X1=ρc, |
X2=ρc2, |
X3=xN2, |
X4=xCO2. |
При определении других термодинамических функций (свойств) используются следующие частные производные коэффициента сжимаемости.
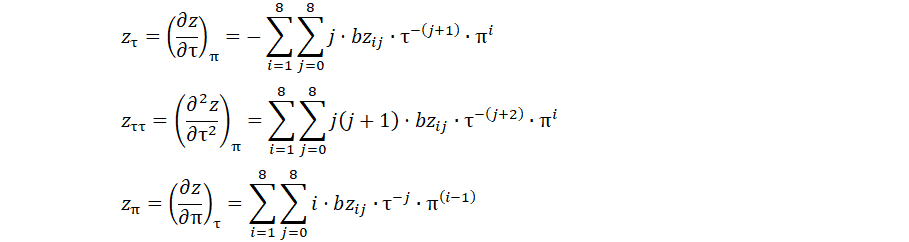
Разработанный метод относится к методам определения термодинамических функций через идеально-газовое состояние. В качестве базовой термодинамической функции в идеально-газовом состоянии используется изобарная теплоёмкость.
Изобарная теплоёмкость, Дж∙кг-1∙K-1
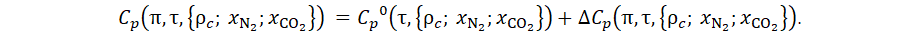
Изобарная теплоёмкость в идеально-газовом состоянии определяется по следующей формуле, разработанной исходя из данных стандарта [5] об изобарной теплоёмкости в идеально-газовом состоянии индивидуальных веществ:

Функция изотермического отклонения изобарной теплоёмкости от идеально-газового состояния определяется через разработанное уравнение состояние:
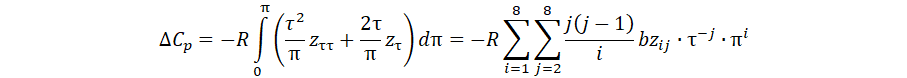
Изохорная теплоёмкость, Дж∙кг-1∙K-1

Коэффициент Джоуля-Томсона, K∙Па-1

Показатель адиабаты

Скорость звука, м∙с-1

Энтальпия, Дж∙кг-1

энтальпия в идеально-газовом состоянии

Функция изотермического отклонения энтальпии от идеально-газового состояния.

Энтропии, Дж∙кг-1∙K-1

энтропия в идеально-газовом состоянии

Функция изотермического отклонения энтропии от идеально-газового состояния.
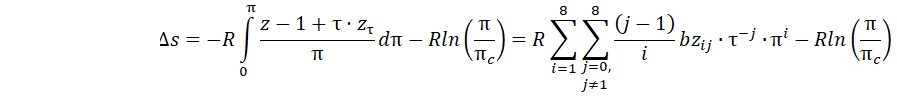
Надо отметить, что для решения основных режимно-технологических задач нет необходимости в определении непосредственно абсолютных значений энтальпии и энтропии, достаточно найти их изменение в протекающем процессе.

В соответствии с требованиями межгосударственного стандарта по обеспечению единства измерения [2], адекватность предлагаемого метода подтверждается анализом результатов расчета термодинамических функций, отклонение которых не должно превышать уровня точности соответствующих термодинамических функций, полученных методом на основе фундаментального уравнения состояния AGA8 (см. [4], [5]). Например, по коэффициенту сжимаемости отклонение не должно превышать 0,2 %.
ТАБЛИЦА 2. Максимальные отклонения расчетных свойств природного газа, %
|
Природный газ |
Δz |
ΔCp |
Δh |
Δs |
|
данные за 2011–20171 |
0,105 |
0,262 |
0,086 |
0,125 |
1 данные по компонентному составу природного газа, транспортируемого в центральном регионе РФ
Метод определения физических свойств природного газа по данным о плотности при стандартных условиях и содержании азота и диоксида углерода
Основой моделирования течения реального газа является критерий подобия – число Рейнольдса, характеризующее соотношение между инерционными силами и силами вязкости (характеризующими физические свойства газа).

Из существующих методов по определению динамической вязкости природного газа наиболее детальным является метод, изложенный в стандарте [6]. Однако применение данного метода возможно при наличии данных о компонентном составе природного газа.
Расчетный метод по неполному компонентному составу стандарта [3] имеет погрешность около 5 %, что соответствует уровню отклонения результатов расчета этого метода от метода по компонентному составу стандарта [6].
Поэтому с целью повышения точности определения динамической вязкости природного газа был разработан предлагаемый расчётный метод в виде следующей функциональной зависимости.
Динамическая вязкость, мкПа∙с

Далее приведено полученное уравнение динамической вязкости природного газа:

Результаты расчёта предлагаемого метода соответствуют результатам метода по компонентному составу [6] в пределах 0,2 %.






