Анализ расходной части бюджета
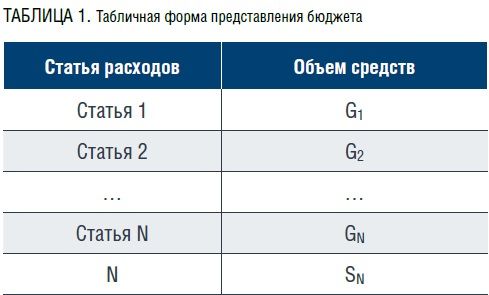
В качестве исходного материала будем использовать расходную часть бюджета экономических систем в виде таблицы (табл. 1), в колонках которой указывается перечень статей и объемы средств.В табл. 1 обозначены: N – число статей, SN – общий объем финансовых средств бюджета, {G} = {G1, G1, …, GN} – ряд значений постатейных расходов. Понятно, что в таком представлении бюджета трудно говорить о возможности какой бы то ни было аналитической обработки его как целого.
Все, что можно сделать, – это определение процентного соотношения отдельных статей по объему акцептованных средств с общими затратами или, например, сравнение однотипных статей в бюджетах различных стран, предприятий и т.п.
Первый шаг: диаграмма Лоренца
Пусть, например, этот числовой ряд имеет вид: 30, 600, 70, 100, 200. Упорядочим выбранный ряд чисел в порядке их возрастания: 30, 70, 100, 200, 600 и рассчитаем ряд накопленных частичных сумм {SN} по формуле:
где n = 1, 2, …, N (в нашем примере N = 5).Затем каждую из полученных накопленных сумм ряда {Sn} = {30, 100, 200, 400, 1000} разделим на сумму всех чисел SN = 1000. Получаем ряд значений {Y} = {0.03, 0.10, 0.20, 0.40, 1.0}, являющихся значениями оси Y диаграммы Лоренца. Соответствующие значения координат по оси X рассчитаем по формуле Xn = n/N, где {n} = {1, 2, 3, 4, 5}. То есть, {Xn} = {0.2, 0.4, 0.6, 0.8, 1.0}. В итоге, откладывая полученные точки (Xn, Yn) внутри квадрата со сторонами, равными единице, получаем диаграмму Лоренца для исходного числового ряда {G} = {30, 70, 100, 200, 600} (рис. 1).
Очевидно, что диаграммы Лоренца позволяют визуально оценить неравномерность распределения любых числовых рядов, отличающихся по числу элементов (N) и общей сумме чисел (SN). Отметим, что данный подход позиционирует любое конкретное распределение между двумя крайними вариантами: равномерным («А» – все числа равны друг другу) и предельно неравномерным («М» – все числа, кроме одного, равны нулю).
Второй шаг: аппроксимация диаграмм Лоренца однопараметрической функцией
В отличие от существующих семейств аппроксимирующих функций [8] нами был сделан выбор однопараметрической функции аппроксимирования L(x,α) в виде:
Аппроксимация диаграмм Лоренца семейством функций L(x,α) [1] позволила ввести параметр α как метрику неравномерности распределения значений соответствующего конкретного числового ряда (рис. 2).
Возможен вопрос: любой ли числовой ряд может быть аппроксимирован функцией (2)?
Разумеется, нет. Однако, как показывает накопленный нами обширный фактический материал, числовые ряды, относящиеся к бюджетам различных уровней (семья, предприятие, целевая программа, страна) с достаточной точностью (дисперсия меньше процента) аппроксимируются именно этой функцией.
Третий шаг: статистическая плотность распределения вероятности
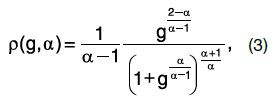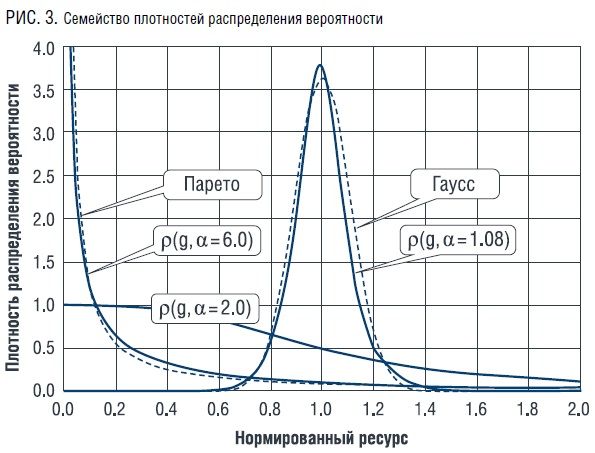
где g – значение расхода {Gn}, нормированное на величину SN/N.Полученная плотность вероятности при значениях параметра неравномерности распределения (α), близкого к равномерному варианту (α ≈ 1.0) и к существенно неравномерному (α >> 2.0), практически совпадает с известными функциями распределения Гаусса и Парето соответственно (рис. 3). Причем для α = 2.0, которому на плоскости диаграмм Лоренца соответствует дуга окружности, полученная плотность вероятности играет роль своеобразной границы, разделяющей семейство р (g, α) на два класса: 1 ≤α< 2 («А») и α > 2 («М»). Более того, кривая р (g, 2.0) – единственная функция, принимающая ограниченное ненулевое значение при g = 0.
Четвертый шаг: обобщенная энтропия числового ряда
Интеграл (4) с функцией распределения (3), к сожалению, в общем случае аналитически не берется и определяется численными методами.На рис. 4 представлен вид нормированной энтропии V(α), полученный методом численного интегрирования формулы (4) [7] и последующей аппроксимацией функции V(α), заданной таблично, аналитической функцией (5):
При этом значение дисперсии аппроксимации составило менее 1 %. Таким образом, нам удалось поставить в однозначное соответствие данные «унылой» бюджетной таблицы (табл. 1) с графиком зависимости V(α) (рис. 4). Это уже, безусловно, осязаемый результат.
Важно, что график зависимости энтропии от параметра неравномерности (α) имеет максимум в точке «Р» ( α = 2.0),который находится между двумя вариантами распределения «А» и «М» в терминах диаграммы (рис. 1).
Слева от точки «Р» производство (дифференциал) энтропии имеет всегда положительное значение (dV ≥ 0), а на правом склоне «купола» производство энтропии всегда отрицательно (dV ≤ 0). Таким образом, в точке «Р» энтропия V(α ) = Vmax и производство dV(α ) = 0.
Бюджетная экономическая система, ее адаптивность и гомеостаз
Бюджетная экономическая системаДо сих пор мы оперировали с неким числовым рядом, имеющим непосредственное отношение к бюджетной таблице (табл. 1).
Безусловно, у нас есть желание в нашем анализе продвинуться дальше, используя основные понятия (адаптивность, гомеостаз), которые введены в научный обиход в работах [9, 5, 10, 11] и во многих других для открытых динамических систем, экономических в том числе.
Бюджет, представленный в виде таблицы (табл. 1) и диаграммы (рис. 1), не является, разумеется, динамической системой, это всего лишь мгновенный фотоснимок, отражающий ее состояние на определенный момент времени.
С другой стороны, бюджет – дело рук человеческих, результат интеллектуального труда большого числа управленцев, анализирующих состояние экономической системы, внешней среды, расставляющих приоритеты, распределяющих соответствующие финансовые ресурсы. Именно управленцы играют роль механизма обратной связи в системе «бюджет + управление бюджетом», привнося в нее извне необходимое количество так называемой отрицательной энтропии, «негэнтропии» [4, 5, 6, 12].
В этом смысле систему «бюджет + управление бюджетом», так сказать, «бюджетную систему», можно, по-видимому, рассматривать, как определенный «нетривиальный» вариант открытой динамической системы. Единственное отличие – это не непрерывное, а дискретное во времени управление системой (как правило, возможные управленческие воздействия происходят не чаще, чем раз в год).
Адаптивность «бюджетной системы»
Возвращаемся к рис. 4. Точка «Р» на этом графике – особая точка, в которой уравновешивается действие двух противоположных по своему смыслу факторов:
• стремление системы к «термодинамическому» равновесию (область α < 2.0, возрастание энтропии с ростом α);
• неравновесная трансформация системы под воздействием управленческих решений, относящихся к расстановке приоритетов и распределению средств (область α > 2.0, уменьшение энтропии с ростом α).
В точке «Р», кроме того, как мы покажем ниже, обеспечивается максимальный из возможных уровень адаптивности «бюджетной системы».
Действительно, в нашем случае адаптивность бюджета – это возможность выбора различных вариантов распределения финансовых средств без изменения макропараметров соответствующих управленческих решений. Энтропия V(α) здесь выступает как метрика адаптивности бюджета [2].
Согласно формуле Л. Больцмана, энтропия физической системы (S) пропорциональна логарифму числа различимых микросостояний (W), которыми может быть реализовано макросостояние некоторой физической системы.
В качестве аналога понятию «физической системы» в рамках нашего подхода будем рассматривать «бюджетную систему».
Макросостояние «бюджетной системы» будем характеризовать:
• отношением (SN/N) объема финансовых средств (SN) к числу статей (N);
• параметром неравномерности распределения (α).
Под микросостоянием бюджета будем понимать конкретный вариант реализации макросостояния «бюджетной системы» с постатейным распределением {G} = {G1, G2, …, GN} финансовых средств по набору статей {N} = {n1, n2, ..., N}.
И, наконец, для полного переноса формулы расчета энтропии физической системы на энтропию «бюджетной системы» нам необходимо научиться считать для каждого макросостояния бюджета число «различимых» микросостояний (W).
В общем случае различимость микросостояний будет обеспечиваться наборами неповторяющихся значений в ряду {G} = {G1, G2, …, GN} и статей {N} = {n1, n2, ..., N}. При этом W будет равно числу вариантов перестановок (W= N!). Например, для N = 2W = 1 ∙ 2, для N = 3W = 1 ∙ 2 ∙ 3 и т.д.
Несложно установить, что совпадение значений в ряду {G} = {G1, G2, …, GN} снижает число различимых микросостояний бюджета. В простейшем случае при равенстве значений {G1, G2, …, GN} все микросостояния идентичны друг другу, поскольку порядок и перестановка статей в этом случае не играют никакой роли.
То есть W = 1. Получаем минимальное значение ln(W) = 0 (нижняя граница области «А»).
Не столь очевиден факт снижения числа различимых микросостояний W для тех вариантов распределения, в которых в ряду {G1, G2, …, GN} имеются совпадающие числа. То есть максимальное разнообразие вариантов (W = N!) при каждом повторении значения числа в исходном числовом ряду уменьшается до (N – n)! где n – число повторов. Более того, в реальных постатейных распределениях бюджета встречаются близкие по значению числа.
Рассматривая близкие числовые значения как условно равные, мы также получаем
соответствующее снижение числа различимых микросостояний (область «М»).
Гомеостаз «бюджетной системы»
По определению, состояние гомеостаза неравновесной системы соответствует состоянию, при котором производная энтропии системы от времени равна нулю или близка к этому значению. В нашем случае о гомеостазе «бюджетной системы» можно говорить (в силу дискретности управления) только в случае, если доступны данные по бюджетам за достаточно продолжительный период времени.
Вероятно, гомеостаз распределения бюджета в точке «Р» соответствует «здоровью» экономической системы, ее высокой степени адаптивности, когда все ее составляющие получают в рамках установленных приоритетов необходимые или приемлемые объемы ресурсов.
Вариативная зона оптимальных решений и энтропийный «компас»
Зона оптимальных решенийИтак, точка «Р» (α = 2.0) и ее ближайшие окрестности на графике V(α) (рис. 4) являются особой зоной состояний «бюджетной системы». Именно в этой области реализуется максимум адаптивности системы, а следовательно, и ее наиболее устойчивое состояние в постоянно изменяющейся внешней среде. Уместна аналогия с гомеостазом живых организмов. «Здоровый» биологический организм, находящийся в состоянии гомеостаза, обладает максимальным из возможных резервом устойчивости в отношении
изменений окружающей среды и все его подсистемы обеспечены необходимыми ресурсами.
Теперь становится более понятным и оправданным стремление управленцев удерживать «бюджетную систему» именно в этой оптимальной зоне. Заметные отклонения системы от точки α = 2.0 вправо или влево существенно увеличивают риски нарушения стабильности существования системы как таковой.
Далее. Для перевода энтропии реальных бюджетов в точку максимальной адаптивности «Р» требуются дополнительные финансовые средства, объем которых зависит от величины и знака отклонения параметра неравномерности распределения от α = 2.0 [11].
На рис. 5 приведен результат расчета минимальной дополнительной суммы (∆S), требующейся для преобразования исходного ряда чисел с произвольным параметром неравномерности распределения в распределение с параметром α = 2.0. Расчетная сумма нормировалась на распределенную сумму. Данный график позволяет определить границы вариативной зоны оптимальных решений для приемлемого значения ∆S.
Так для значения ∆S = 10 % вариативная зона оптимальных решений ∆α = [1.86, 2.08] (рис. 5).
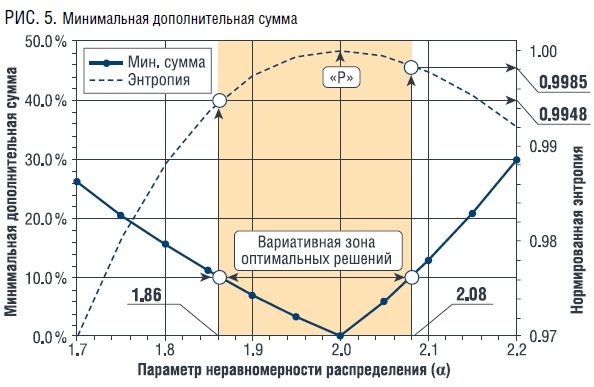
Соответственно размерам вариативной зоны оптимальных решений на графике зависимости энтропии от параметра можно определить снижение энтропии бюджета:
• 0.9985 в зоне «М» (0.15% от Vmax);
• 0.9948 в зоне «А» (0.52% от Vmax).
Альтернативный способ возвращения системы в оптимальную зону – перераспределение имеющихся средств между статьями. Однако на практике это сделать не так просто. Например, если в предыдущий период были сделаны серьезные финансовые вливания в программу модернизации армии, рассчитанную на несколько лет, вы не можете резко уменьшить финансирование соответствующих статей бюджета на текущий период, не поставив успех реализации программы в целом под вопрос.
Энтропийный «компас»
Для большей чувствительности предлагаемого метода анализа бюджета используем выражение для производства энтропии:
На рис. 6 приведена зависимость производства энтропии от параметра неравномерности распределения бюджета, обладающая большей крутизной реакции на изменения неравномерности бюджета в окрестности точки «Р», чем зависимость энтропии от α (5).
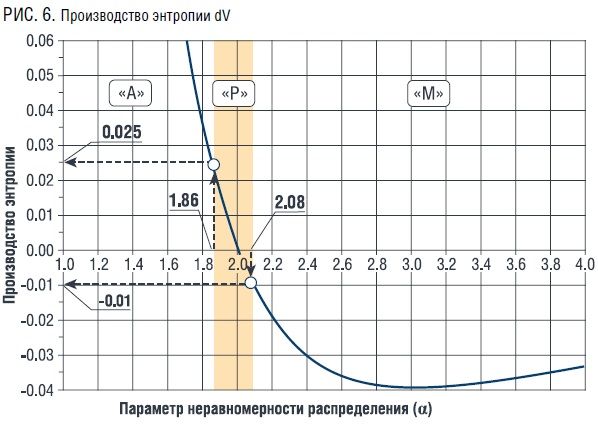
Кроме того, в отличие от «купола» энтропии (рис. 4) данный график (рис. 6) дает однозначное соответствие значений и знака dV для различных отклонений неравномерности распределения бюджета от точки «Р»:
• положительное значение производства энтропии соответствует значениям неравномерности распределения зоны «А» ( α < 2.0);
• отрицательное значение производства энтропии соответствует значениям неравномерности распределения зоны «М» (α > 2.0).
Из этого графика также легко можно определить границы зоны оптимальных решений в терминах производства энтропии [-0.010, +0.025].
Альбом результатов исследования реальных бюджетов
В следующих примерах (рис. 7 – 20) приведены результаты расчета обобщенной нормированной энтропии и производства энтропии фактических ежегодных распределений бюджетных средств разных стран по функциональным статьям верхнего уровня.Отметим, что в приведенных реальных примерах энтропия и ее производство испытывают
постоянные отклонения от точки равновесия «Р». По‑видимому, отклонения от этой точки вызываются множеством объективных и субъективных факторов.
Наш подход, по сути, предоставляет только некий индикатор («компас») для анализа изменений энтропии «бюджетной системы», не более, но и не менее того.
В этой связи детальную трактовку приведенных результатов по бюджетам разных стран и, в частности, сопоставление этих результатов с крупными социально-политическими событиями в отдельных странах и в мире в целом мы оставляем на усмотрение читателя.
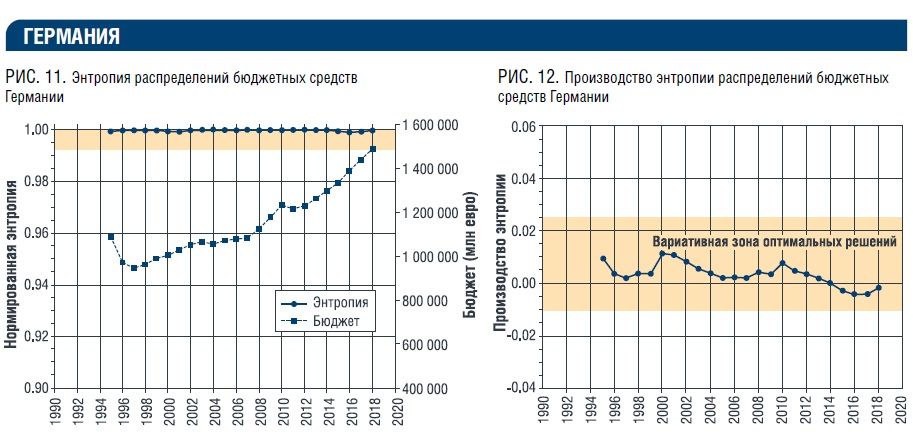
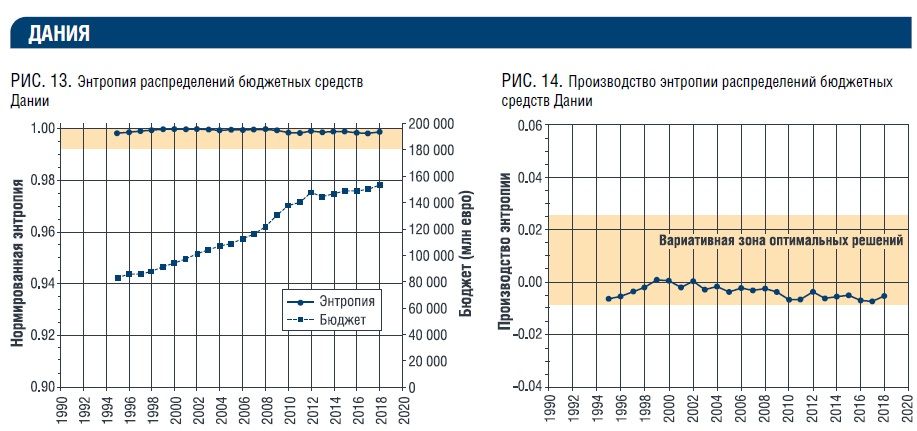
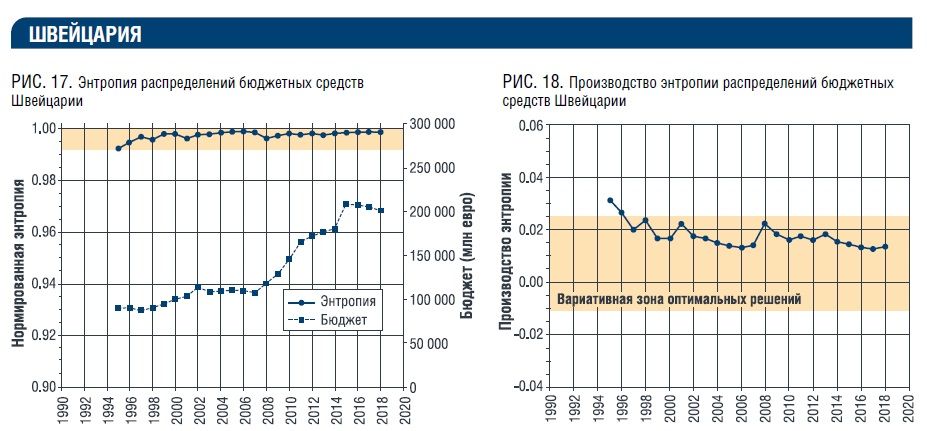
Данные, приведенные на рис. 7 – 20, интересно сопоставить с данными рейтинга стран по индексу качества/уровня жизни. Индекс качества жизни включает в себя такие показатели, как стоимость жизни, покупательная способность, соотношение цены недвижимости к доходу, время движения на работу, уровень безопасности/преступности, загрязнение окружающей среды, качество здравоохранения, климат.
В табл. 2 представлены страны, бюджет которых мы исследовали в нашей статье, и указан номер места, которое занимает страна в этом рейтинге.
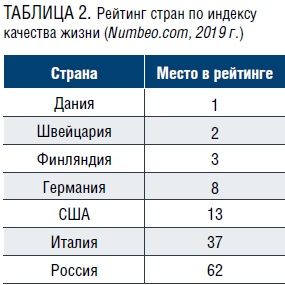
Нетрудно заметить, что наши данные, отражающие качество управления «бюджетной системой», весьма выразительно корреспондируются (хотя и не на 100 %) с данными рейтинга по качеству/уровню жизни.
Например, данные по Италии (рис. 19, 20 и табл. 2) явно не показывают такой корреляции. Вероятно, это связано с тем, что абсолютный объем бюджетных средств (в расчете на одного гражданина) в Италии составляет только 50 % от аналогичной цифры в Дании.
Для рейтинга качества жизни, разумеется, абсолютные значения распределяемых средств имеют не меньшее значение, чем качество управления самой «бюджетной системой».Словом, хорошее управление и достаточно денег – замечательно, хорошее управление и недостаточно денег – перспективно, плохое управление и недостаточно денег – тупик!
Заключение
Основным результатом данной статьи можно считать презентацию профильным специалистам методики анализа бюджетов различных уровней с использованием энтропийной функции «бюджетной системы».Фактически, данный инструмент позволяет проложить продуманную траекторию в управлении бюджетами и заблаговременно оценивать риски возникновения кризисных ситуаций в самой экономической системе.
Литература
1. Крянев А.В., Матохин В.В. и Климанов С.Г. Статистические функции распределения ресурсов в экономике. М.: Препринт МИФИ, 1998. 2. Крянев А.В., Матохин В.В., Харитонов В.В. Энтропийный метод мониторинга реализации экономических систем // Экономические стратегии, 2010. № 5, С. 58–63.
3. Матохин В.В. «Золотая пропорция» управленческих решений // Электроника, 1997. Т. 3–4. С. 99–102.
4. Прангишвили И.В. Системный подход и системные закономерности. М.: СИНТЕГ, 2000.
5. Пригожин И.Р. Конец определенности. Время, хаос и новые законы природы. Ижевск: НИЦ «Регулярная и хаотичная динамика», 2000. С. 208.
6. Лийв Э.Х. Инфодинамика. Обобщенная энтропия и негэнтропия. Таллин, 1998.
7. Antoniou I. Analysis of resources distribution in economics based on entropy / I. Antoniou, V. V. Ivanov, Y. L. Korolev, A. V. Kryanev, V. V. Matokhin, Z. Suchaneckia // Physica A, 2002. Vol. 304, P. 525–534.
8. Sarabia J. M., Castillo E., Slottje D. J. An ordered family of Lorenz curves // Journal of Econometrics. Elsevier Science S.A., 1999. Vol. 91. P. 43–60.
9. Bertalanffy L. General System Theory. New York: George Braziller lnc., 1969. P. 1–289.
10. Beer S. Brain of the Firm. Wiley, 1972.
11. Haritonov V. V., Kryanev A. V., Matokhin V. V. The adaptable potential of economic systems // International Journal of Nuclear Governance, Economy and Ecology, 2008. Vol. 2. P. 131–145.
12. Schredinger E. What Is Life? Cambridge University Press, 1944.
