Большая часть нефтегазовых месторождений разрабатываются с помощью системы поддержания пластового давления (ППД). ППД организуется закачкой рабочего агента (вода, газ или нефть) в разрабатываемый пласт, увеличивая тем самым добычу углеводородов (с помощью процессов вытеснения) и поддерживая пластовое давление на некотором уровне. Чаще всего закачиваемый агент — вода, как самый доступный и дешевый вид закачиваемого агента. Неконтролируемый процесс закачки воды в пласт может приводить к снижению добычи нефти. Одним из примеров такого вида является преждевременное обводнение продукции добывающих скважин из-за прорыва закачиваемой воды из нагнетательной скважины. Как правило такой процесс возникнуть по двум причинам: 1 – объем закачиваемой в нагнетательную скважину воды слишком велик, что приводит помимо увеличения пластового давления к прорывам воды в добывающую скважину и 2 причина — неоптимальный отбор жидкости из добывающей скважины сопровождающийся превышением критического значения депрессии, приводящий к быстрому конусообразованию и повышению обводненности продукции.
На практике при разработке месторождений с системой ППД, оптимальные режимы работы нагнетательных и добывающих скважин, исключающие процессы конусообразования и нежелательный прорыв воды в добывающих скважинах, рассчитывают с помощью гидродинамической модели. Такой подход имеет ряд недостатков главный из которых является времязатратность. Даже имея абсолютно точную гидродинамическую модель, корректно описывающую все физические процессы фильтрации в пласте, нужно потратить большое количество времени чтобы определить оптимальные режимы для нагнетательных и добывающих скважин. Поэтому в данный момент важной задачей является создание инструмента, который бы с допустимой точностью (сопоставимой с ГДМ) и приемлемой скоростью рассчитывал оптимальные режимы работы скважин. В основе такого инструмента могут быть использованы зарекомендовавшие себя принципы нейросетевого моделирования.
В работах (Vershinin et al.,2020) и (Vershinin et al.,2021) было показано что обученные нейронные сети позволяют воспроизводить технологические режимы работы добывающих и нагнетательных скважин на периоде до 10 лет со средней ошибкой менее 5%. В работе (Vershinin et al.,2021) был приведен нейросетевой алгоритм решения задачи оптимального управления добычей на примере группы скважин, расположенных в подгазовой зоне. Оптимальный режим управления добычей, найденный с помощью нейронной сети совпал с оптимальным режимом , найденным методом прямого гидродинамического моделирования в пределах погрешности обоих методов. При этом время нахождения оптимального режима добычи нейронной сетью оказалось на два порядка меньше, чем при использовании ГДМ .
Приведенные выше результаты указывают на возможность использования алгоритмов нейросетевого моделирования при решении задач прогнозирования добычи и оптимизации режимов заводнения нефтегазовых месторождений.
Целью данной работы является исследование возможности прогнозирования обученной нейронной сетью режимов работы добывающих нефтяных скважин, моментов прорыва воды в процессе заводнения участка.
Постановка задачи. Исходные данные для обучения
Модель содержит 10 добывающих и 8 нагнетательных скважин. Тернарная диаграмма насыщенностей отображена на рисунке1. Через центр залежи проходит два гидродинамических разлома, которые позволяют условно разделить месторождения на 3 сектора.

Данное месторождение является примером законтурного заводнения: все нагнетательные скважины расположены за контуром водонефтяного контакта.
Исходными данными для обучения нейросетевой модели (обучающей выборкой), являются результаты прогнозирования на гидродинамической модели. Обучающая выборка была создана на основании 16 различных режимов работы скважин, периодом 7,5 лет. Нейронная сеть в процессе обучения должна была выявить взаимосвязь между: а) забойным давлением и дебитом нефти и воды на каждой добывающей скважине и б) режимом работы каждой скважины и режимами работы соседних скважин. Взаимосвязь под пунктом б можно разделить на три вида влияния: влияние в системе скважин «добывающая — добывающая», влияние в системе «нагнетательная — добывающая» и влияние в системе «нагнетательная — нагнетательная скважина».
Дополнительно были сгенерированы 10 тестовых режимов для проверки качества прогнозирования нейронной сети. Период прогнозирования совпадает с режимами в обучающей выборке и равен — 7,5 лет.Входными параметрами для обучения нейронной сети являлись:
-
Дебит нефти
-
Дебит жидкости
-
Забойное давление
-
Приемистость (для нагнетательных скважин)
Приемистость нагнетательных скважин подобрана так, чтобы скомпенсировать отборы добывающих скважин в целом по месторождению, то есть обучение нейронной модели производилось в режиме полной компенсации отборов.
Базовая модель. Алгоритм обучения
С математической точки зрения, задача обучения нейросетевой модели с целью установления всех значимых физических взаимосвязей, относится к задаче аппроксимации временных рядов. Такую задачу чаще всего решают с помощью нейронных сетей специального вида — рекуррентных нейронных сетей. Так как процессы фильтрации реального месторождения, могут характеризоваться инертностью процесса, то влияние скважин друг на друга может происходить с некоторой временной задержкой. Для решения подобных задач лучше всего использовать рекуррентную сеть вида Long Short-Term Memory (LSTM). Благодаря своей структуре, приведенной на рисунке3, LSTM позволяет связывать между собой события в обучающей выборке разделенные некоторым, заранее неизвестным временным лагом и использовать установленные взаимосвязи в дальнейшем для прогнозирования.

В работах (Vershinin et al.,2020) и (Vershinin et al.,2021) авторы использовали LSTM для прогнозирования технологических режимов работы добывающих и нагнетательных скважин. Средняя ошибка при этом составила менее 5% на периоде 10 лет. Алгоритм обучения модели LSTM соответствует работе (Vershinin et al.,2020).
Результаты обучения
После обучения моделей на оптимальном наборе гиперпараметров, была проведена валидация моделей. Значения loss – функции и точность нейронных моделей приведена в таблице 1.

По результатам валидации можно сделать вывод, что нейронная модель успешно обучились. Т.е был найден оптимальный набор весовых коэффициентов для достоверной аппроксимации большинства входных векторов. Дальнейшая проверка качества обучения непосредственно связана с прогнозированием тестовых режимов работы на обученной модели LSTM и сравнением со значениями, рассчитанными на гидродинамической модели.
Прогнозирование
Алгоритм прогнозирования в целом совпадает с алгоритмом, представленным в работе (Vershinin et al.,2020). Прогноз рассчитывается на основе технологических режимов работы добывающих скважин за N шагов (месяцев). Значение N совпадает с количеством шагов входного вектора нейронной модели. Далее с помощью обученной нейронной сети, рассчитывается выходной вектор–режим скважин на следующий месяц. К исходной выборке данных добавляются новые рассчитанные значения. Последующий прогноз рассчитывается уже с учетом предсказанных на предыдущем шаге значений. Алгоритм выполняется до тех пор, пока не будет достигнуто окончание заданного периода прогнозирования. Следует отметить, что на каждом шаге прогнозирования значения управляющих параметров считаются известными и подаются на вход нейронной сети. Это позволяет в дальнейшем варьировать их значения при поиске оптимального режима.
Тестирование точности прогнозирования сети LSTM проводилось в сравнении с тестовыми режимами (10 режимов), полученными гидродинамическим моделированием. Качество прогнозирования оценивалось по величине средней относительной ошибки на периоде 7,5 лет. Все результаты качества прогнозирования по каждой скважине и по каждому режиму приведены в таблице 2. Нагнетательные скважины I1-I8. Остальные скважины -добывающие. Расположение скважин по участку приведено на рисунке 1.

При анализе результатов была построена гистограмма распределения средней относительной ошибки (Рисунок 4).

В большинстве случаев средняя относительная ошибка по скважинам не превышает 5%.
В 10 % случаев ошибка составляет от 5 до 12 % и по 0,7% случаев ошибка составляет около 20 %.
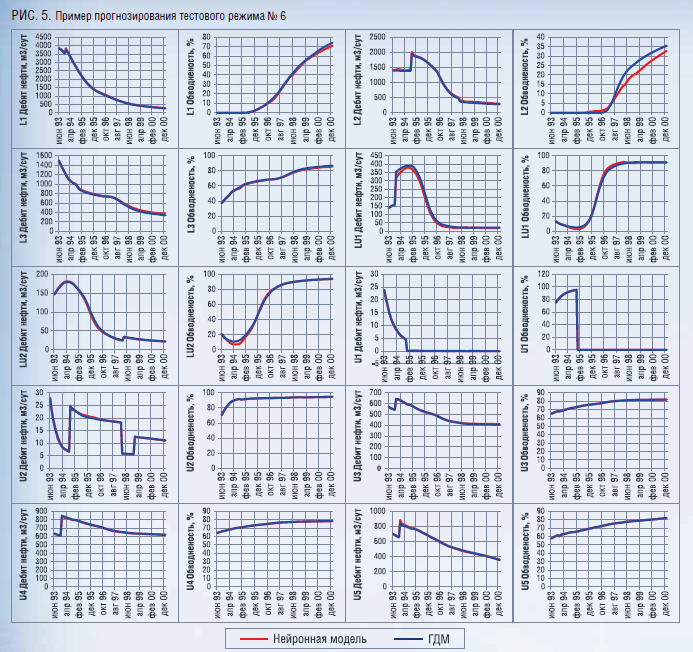
В качестве примера прогнозирования приведен график по дебиту нефти и обводнености продукции добывающих скважин по тестовым режимам №1 (Рисунок 5)
Также следует отметить, что время расчета одного тестового режима на гидродинамической модели составляет около 2 минут, а расчет проведённый с помощью LSTM - занимает 13 секунд, что в 9 раз быстрее. Как видно из рисунков 5 и 6 нейронная сеть с высокой точностью воспроизводит как дебит нефти, так и обводненность продукции на добывающих скважинах. Это касается, как самого уровня обводненности, так и момента прорыва воды, что позволяет сделать вывод о принципиальной возможности построения алгоритмов оптимизации режимов работы в системе «добывающие-нагнетательные» скважины на основе обученной нейронной сети. Как правило в таких алгоритмах блок вычисления параметров добычи выступает в виде «черного ящика», которому на вход подаются управляющие параметры, сгенерированные алгоритмом оптимизации. Само содержание черного ящика не существенно. Главное требование к нему- точность и быстрота отклика-нахождения решения. Нейронная сеть при должной точности прогноза будет предпочтительней в силу большей скорости расчета
Заключение
Исследована точность прогнозирования режимов работы добывающих и нагнетательных скважин с помощью обученной нейронной сети LSTM в задаче добычи нефти с системой ППД. Задача прогнозирования решалась как задача прогнозирования временных рядов. Достигнутая точность прогнозирования позволяет использовать обученную нейронную сеть для прогнозирования реальных параметров работы скважин. Высокая скорость расчета и точность прогнозирования позволяет встраивать нейронную сеть в систему управления месторождением и применять ее в задачах оптимизации режимов работы скважин.






