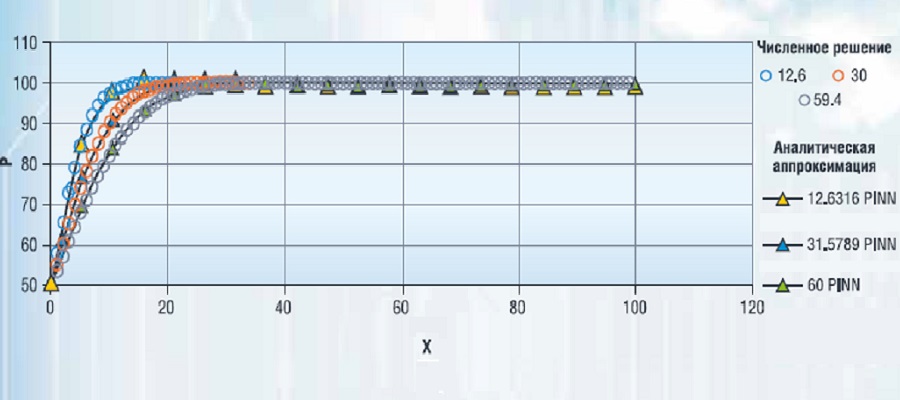
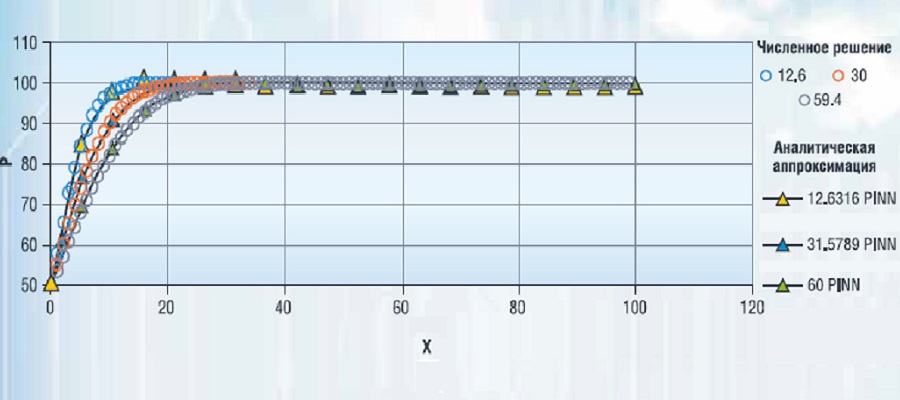
Различные реализации методы машинного обучения с каждым днем все активнее применяются для решения задач, связанных с прогнозированием и оптимизацией технологических процессов. Нейронные сети определяют наличие сложных функциональных взаимосвязей между параметрами и в дальнейшем позволяют использовать полученную информацию для прогнозирования. В свою очередь, относительная простота вычислительной архитектуры нейронной сети значительно сокращает время вычисления прогнозных вариантов, что позволяет использовать ее в решении задач оптимизации закачки системы поддержания пластового давления (ППД).
Эффективное управление системой ППД является актуальной задачей для инженера-разработчика. Регулирование закачки нагнетательного фонда скважин – способ поддержания и увеличения базовых уровней добычи нефти на промысле. На месторождениях, находящихся на IV стадии разработки, оптимизация системы ППД остается одним из рентабельных способов увеличения нефтедобычи. Процесс управления заводнением характеризуют следующие особенности:
- Процесс заводнения – это инерционный процесс, характеризующий отклик по жидкости добывающей скважины на изменение закачки нагнетательной скважины, спустя определенный период времени – временной лаг;
- Динамика добычи нефти – нестационарный процесс, зависящий от выработки запасов;
- Наличие взаимосвязи между скважинами.
Данные особенности обуславливают выбор инструментов, которые применимы для управления процессом заводнения. Постановка задачи по оптимальному распределению закачки звучит следующим образом: определить такие целевые значения объемов закачки на каждой нагнетательной скважине, которые позволят максимизировать добычу нефти. Трудоемкость поставленной задачи связана с большим количеством фонда на месторождениях и, соответственно, огромным количеством вариантов распределения закачки при текущих инфраструктурных ограничениях. В этих условиях поиск оптимального варианта становится нетривиальной задачей.
Методы управления закачкой на нефтяных месторождениях
Распространенными инструментами, способными решать задачи регулирования закачки на нагнетательных скважинах, являются 3D геолого-гидродинамические модели, 2D прокси-модели, CRM-модели и экспертный анализ. Рассмотрим преимущества и ограничения каждого из них.
Геолого-гидродинамическое моделирование (ГДМ) потенциально является наиболее точным и физически содержательным инструментом при условии отсутствия неопределенностей по части геологии, т.е. если предположить, что все параметры продуктивной залежи известны, то, адаптировав ГДМ, можно выполнить многовариантные расчеты с заданием разных уровней закачки на каждой нагнетательной скважине и тем самым определить оптимальные режимы для максимизации добычи нефти на залежи. Однако отсутствие надежной и детальной информации о природных пластах и некорректность обратной задачи адаптации модели на историю разработки [10] накладывают ограничения в возможности решения поставленной задачи в ГДМ. Также важным ограничением является высокая трудоемкость построения и время счета ГДМ, что также ограничивает применение данного инструмента при решении оперативных задач регулирования закачки.
Прокси-моделирование – по сравнению с традиционными трехмерными гидродинамическими моделями, применяется уменьшение размерности и упрощенное описание физических пластовых процессов [10]. За счет таких упрощений снижается трудозатратность построения моделей и времязатратность на расчеты. Однако в этом случае инструмент становится менее точным и универсальным по сравнению с ГДМ (невозможность воспроизведения прорывов воды по высокопроницаемым каналам, подтягивание конусов воды и т.д.), а ограничения, связанные с неопределенностью по геологии месторождения, не нивелируются.
Одним из примеров прокси-модели является модель CRM, представляющая собой аналитическое решение уравнения материального баланса и позволяющая спрогнозировать динамику дебита жидкости при различных уровнях закачки [9]. Использование CRM имеет хорошие перспективы для решения поставленной задачи. Инструмент позволяет оперативно выявлять нагнетательные скважины с максимальным влиянием на добывающие скважины и решать задачу по перераспределению закачки. На текущий момент основным ограничением является применение сторонней модели обводненности, которая не всегда воспроизводит физически корректные результаты.
Альтернативным способом расчета оптимальных режимов работы нагнетательных скважин является применением нейросетевого моделирования [5, 11]. Нейросетевое моделирование – это метод машинного обучения, ключевой особенностью которого является процесс самообучения на экспериментальных данных. Нейронные сети – универсальный инструмент, и при достаточном количестве нейронов сеть способна аппроксимировать непрерывную функцию любой сложности [7]. При этом скорость вычисления остается высокой за счет относительной простоты математической структуры сети.
Методы нейросетевого моделирования могут быть успешно применимы при:
• наличии неявных взаимосвязей между параметрами;
• наличии большого объема суточных замеряемых данных.
Нейронные сети показывают успешные результаты в прогнозировании временных рядов и в моделировании и оптимизации динамики технологических показателей работы добывающих скважин как на синтетических [2, 6], так и на реальных данных [1, 3, 8].
Ограничением метода являются высокие требования к исходному объему данных. Для получения качественных результатов требуется достаточно разнообразная и достоверная обучающая выборка. Вторым ограничением является невозможность достоверного прогнозирования за пределами обучающей выборки, т.к. метод в классическом представлении использует только статистические закономерности, выявленные в обучающей выборке, и не содержит в себе никакой дополнительной информации о физике процесса.
На текущий момент, несмотря на разнообразие инструментов для управления закачкой, наиболее распространенным способом определения оптимальных уровней закачки на зрелых месторождениях остается экспертный анализ с использованием аналитических инструментов на базе Excel или собственного программного обеспечения (например, ПО РН-КИН, применяемое в компании «ПАО «НК Роснефть»). К основным ограничениям можно отнести высокую трудоемкость подхода и, как следствие, относительно низкую оперативность принимаемых решений, а также зависимость результата от опыта и компетенций инженера.
Исследование применимости нейронных сетей с различными архитектурами для решения поставленной задачи
Выбор архитектуры нейронной сети является важным подготовительным этапом моделирования. Выбрать оптимальную модель можно двумя способами: 1) с помощью непосредственного тестирования различных видов нейронных моделей, с последующим анализом получившихся результатов и 2) исходя из инженерного анализа моделируемых процессов.
В первую очередь проанализирована специфика моделируемых процессов. Заводнение пласта – это инерционные процессы: изменение режима закачки на нагнетательной скважине отражается на динамике добывающей скважины через некоторое время – временной лаг. Такого рода задачи способны решать рекуррентные нейронные сети, а именно модели LSTM (Long Short Term Memory) и GRU (Gates Recurrent Unit).
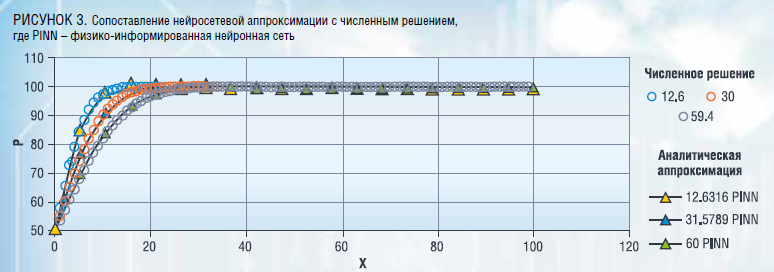
Для подтверждения приведенного выше вывода проведено моделирование обводненности по двум скважинам в разных гидродинамических условиях: в высоко- и низкопроницаемых коллекторах. Проницаемость влияет на инерционность процессов – на низкопроницаемых коллекторах (10 мД) влияние между скважинами распространяется медленнее, чем на высокопроницаемых (200 мД). На рисунках 1–2 приведены примеры моделирования обводненности различными архитектурами нейронных сетей.
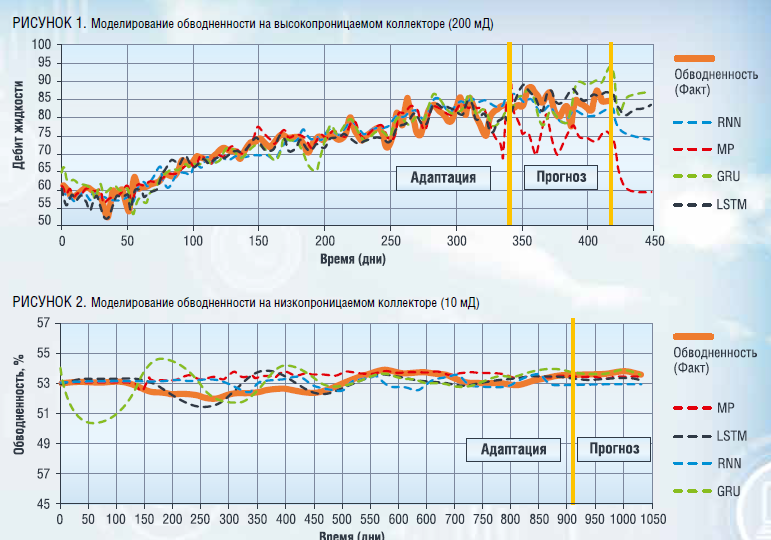
Значительное преимущество рекуррентных нейронных сетей (LSTM и GRU) заметно на низкопроницаемых коллекторах, где инерционность процессов значительно выше. Рекуррентные нейронные сети, обладающие внутренней памятью, воспроизводят тренды изменения обводненности в зависимости от изменения закачки на нагнетательной скважине. Две другие модели – многослойный персептрон и RNN – не способны установить взаимосвязь между режимами закачки и обводненностью добываемой продукции из-за продолжительного запаздывания реакции между изменением режима закачки на нагнетательной скважине и изменением дебитов жидкости и нефти на добывающей.
Таким образом, рекуррентная нейронная сеть LSTM – перспективный метод для решения задач прогнозирования и оптимизации технологических процессов разработки месторождений. Однако у модели LSTM остаются ограничения, присущие всем нейронным сетям, а именно: при обучении в явном виде не учитывается физическая составляющая процесса, как следствие, модели не могут прогнозировать за пределами обучающей выборки. Наиболее критично это проявляется при обучении на малом наборе реальных данных – в ходе обучения могут возникать нефизические зависимости между параметрами.
Разработка физико-информированных нейронных сетей
Одним из возможных вариантов нивелирования, описанных ограничений является применение физико-информированных нейронных сетей [14]. Ключевой особенностью метода является учет при обучении нейронной сети математической модели фильтрации. В целевой функционал обучения добавляется дополнительно слагаемое, описывающее физику процесса.
Применим данный подход для моделирования притока дебита жидкости в добывающую скважину. Основным корректирующим уравнением будет использоваться дифференциальное уравнение распространения давления в упругой среде – уравнение пьезопроводности. Задача обучения нейронной сети формируется следующим образом: смоделировать пластовое давление [13] так, чтобы при расчете дебита жидкости через уравнение притока расчетный дебит жидкости соответствовал фактическому замеру, аналитический вид нейронной сети должен максимально удовлетворять решению уравнения пьезопроводности. Математическая форма записи итогового функционала обучения представлена ниже:
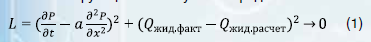
При таком подходе изменяется процедура обучения нейронной сети: веса модели рассчитываются так, чтобы воспроизвести фактическую динамику прогнозных показателей в соответствии с физическими законами явления, записанного в виде дифференциальных уравнений (уравнения пьезопроводности).
Проверка выполнения уравнения пьезопроводности с помощью нейронной сети производится с помощью прямой операции дифференцирования. Допустим, задача решается моделью двухслойного персептрона с гиперболическим тангенсом в роли функцией активации. Математическая форма записи такой модели записывается вот так:
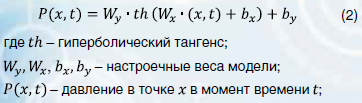
Тогда производные t и х, для подстановки в уравнение пьезопроводности будут выглядеть следующим образом:
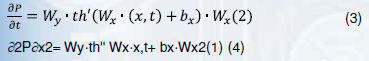
Стоить отметить, что если в функционале (1) убрать слагаемое с фактическими замерами дебита жидкости, то нейронная сеть в процессе обучения аппроксимирует решение уравнения пьезопроводности:
Описанная выше концепция легла в расчетное ядро инструмента для управления заводнением. В основе расчетного ядра лежат две модели нейросетевого моделирования:
· Первая модель – физико-информированная нейронная сеть для моделирования притока жидкости к добывающей скважине, которая основана на модели многослойного персептрона и позволяет моделировать распространение пластового давления через аппроксимацию уравнения пьезопроводности. Используя рассчитанные значения по пластовым и забойным давлениям, через уравнение притока рассчитывается дебит жидкости добывающей скважины. Параметры пласта, коэффициент продуктивности, коэффициент пьезопроводности подбираются в ходе обучения модели.
· Вторая модель – рекуррентная нейронная сеть LSTM для моделирования динамики обводненности продукции: модель позволяет учитывать временной лаг между параметрами и позволяет получить точный прогноз обводненности продукции до 90 дней.
В комплексе две модели образуют математический аппарат, позволяющий оперативно и более точно спрогнозировать и оптимизировать процессы заводнения пласта. Обозначенный гибридный подход при обучении нейронной сети позволяет усилить классическое обучение на данных с помощью математического аппарата физики фильтрации и повысить длительность и качество прогнозирования.
Описание разработанного прототипа на основе нейронных сетей
Для решения поставленной задачи был разработан прототип инструмента «АвтоБаланс» с набором различных модулей с целью апробации использования технологий машинного обучения для управления системой ППД.
Инструмент состоит из 4 основных модулей:
Модуль кластеризации скважин
Кластеризация предназначена для составления списков потенциально влияющих скважин на основании их геометрического расположения. Формирование кластеров осуществляется на основе применения алгоритма построения ячеек Вороного [12].
Входными данными для работы алгоритма являются координаты скважин (координаты точки входа в коллектор (Т1), координаты точки забоя скважин (Т3)) и характер скважин. Координаты Т3 требуются для корректного поиска горизонтальных влияющих скважин.
Для ячейки Вороного рассматриваемой скважины определяются ячейки, имеющие с ней общие точки. Скважины, по которым сформированы граничащие ячейки, формируют список скважин первого ряда. Для ячеек скважин первого ряда определяются ячейки, имеющие с ними общие точки (ячейка рассматриваемой скважины исключается). Скважины, по которым сформированы такие ячейки, формируют список скважин второго ряда.
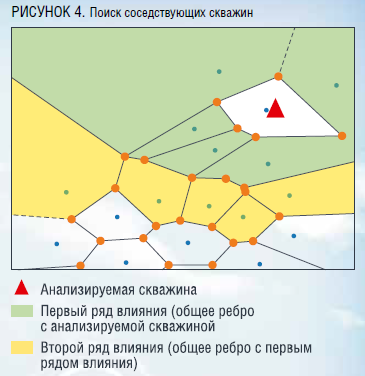
Для горизонтальных скважин поиск влияющих скважин производится из двух точек (Т1 и Т3). Алгоритм поиска не изменяется. Таким образом, расчетный кластер нейросетевой модели может состоять из скважин первого и второго ряда влияния, выбор учета ряда влияния осуществляется вручную.
Модуль интеллектуальной обработки данных
В реальности данные, передаваемые с замерных устройств (ТМС) очень зашумленны: в динамике наблюдается большое количество искаженных замеров, не связанных ни с физическими процессами фильтрации флюидов, ни с процессами разработки месторождения. Такого рода «шумы» в исходной динамике могут привести к неустойчивому процессу адаптации прокси-модели и, как следствие, к низкой прогностической способности нейросетевой прокси-модели месторождения.
Данный модуль фильтрует и сглаживает исходную динамику для повышения качества обучения нейронных сетей. В рамках работы «шум» определяется как необъяснимое изменение целевого параметра, которое не вызвано процессом эксплуатации скважины и не связано с физическими процессами фильтрации. Следовательно, результатом оптимальной фильтрации и сглаживания является обработанный сигнал, где все изменения целевого параметра скоррелированы (объяснены) с помощью других зависимых величин. Для выявления взаимосвязанных трендов в динамике используется метод нейросетевого моделирования. Суть метода заключается в том, что перед запуском статистической обработки данных производится обучение нейросетевой модели на «сырых» данных. В процессе обучения нейросетевая модель устанавливает наиболее вероятные взаимосвязи параметров и воспроизводит объяснимые тренды изменения параметров (базовое решение).
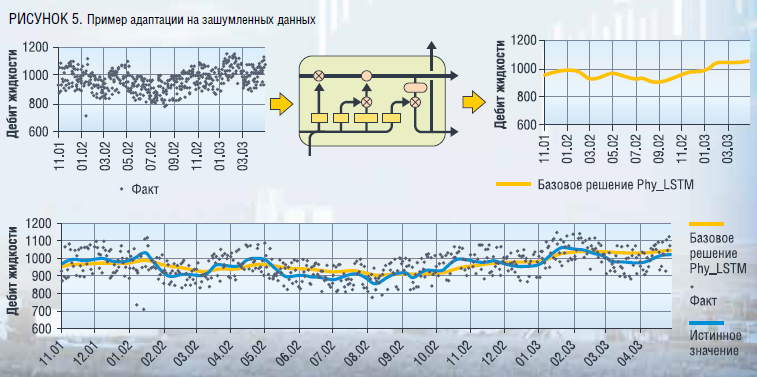
На следующем этапе подбираются параметры сглаживания стандартных статистических методов обработки данных (фильтр Кальмана, вейвлет-преобразование и другие) для достижения максимальной корреляции обработанного сигнала и базового решения по фильтрации (нейросети), но при этом обработанный сигнал не должен терять связь с фактической исходной динамикой. То есть математическая постановка задачи фильтра – подобрать параметры сглаживания для минимизации значения параметра α, который определяется как:
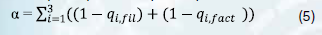
где – коэффициент корреляции Пирсона по отношению сглаженной динамики к базовому решению (нейросети);
– коэффициент корреляции Пирсона по отношению сглаженной динамики к исходной.
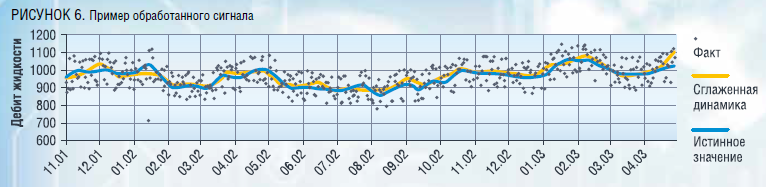
В качестве алгоритма по сглаживанию данных предлагается использовать метод вейвлет-преобразования, т.к. метод имеет математически обоснованные границы эффективного сглаживания (max_level) в зависимости от выбранного вейвлет-базиса:
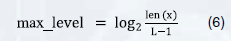
где len(x) – длина исходного сигнала, L – длина вейвлет фильтра.
Модуль автоадаптации нейросетевой прокси-модели
Модуль в автоматизированном режиме создает и обучает нейросетевую модель на подготовленном массиве данных [4]. Обучение проводится по двум различным моделям: дебит жидкости обучается с помощью модели PINN (физико-информированная нейронная сеть), а обводненность – с помощью модели LSTM. В процессе работы модуля рассчитываются оптимальные весовые коэффициенты моделей и определяются гиперпараметры процесса обучения сети. В конце работы модуля формируются обученные нейросетевые модели по каждому сформированному кластеру, с центром в добывающей скважине.
Модуль расчета оптимизации закачки в нагнетательных скважинах
Модуль в автоматизированном режиме формирует диапазон поиска оптимальных уровней закачки воды по каждой нагнетательной скважине. Диапазон ограничен историческими показателями работы скважин и возможностью наземной инфраструктуры системы ППД: максимум закачки определяется по наличию штуцера и по анализу перепада давления между давлением на кусте и устьевым давлением в скважине. Также модуль позволяет задать суммарные ограничения добычи и закачки по отдельным кустам, группам и месторождению в целом.
Оптимальные уровни закачки рассчитываются с помощью оптимизационного алгоритма имитации отжига [15]. Целевая функция оптимизации – накопленная дополнительная добыча нефти.
Принципиальная схема взаимодействия модулей в прототипе представлена на рисунке 7
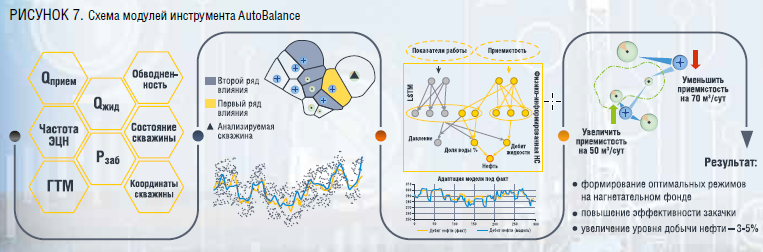
Для тестирования реализованных алгоритмов была использована методика, описанная специалистами ООО «ТИНГ» в статье «Методика тестирования алгоритмов прокси-моделирования» [2]. В основе методики лежит проверка способности прокси-модели оптимизировать режимы нагнетательных скважин, работающих в различных сценариях разработки. Всего в статье приведено 9 сценариев и 9 тестовых гидродинамических моделей. Сценарии охватывают различные варианты эксплуатации: эксплуатация с геологическим разломом, эксплуатация с изменением забойного давления, эксплуатация с шумными замеренными данными, эксплуатация с авто-ГРП и остановками добывающих скважин.
Успешность оптимизации определяется исходя из следующих критериев:
1. Рассчитанный суммарный прогнозный дебит нефти по оптимальному варианту нейросетевой модели не должен отличаться больше, чем на 10 % от прогнозируемого значения по ГДМ.
2. Оптимальные режимы работы нагнетательных скважин, полученные на прокси-модели, должны обеспечивать вариант лучший, чем базовый, т.е. суммарный по скважинам дебит нефти в оптимальном варианте должен быть больше, чем в базовом варианте.
Тестирование на синтетических данных
На первом этапе тестируется способность модели адаптироваться на фактическую динамику добывающей скважины. На рисунке 8 представлен пример ретроспективного прогноза по одной из скважин.
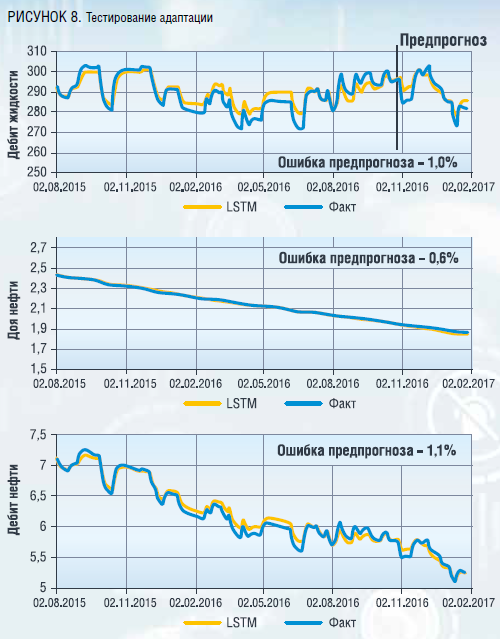
Следующим этапом тестирования является расчет оптимизации. Оптимизация закачки была рассчитана в 9 сценариях работы скважин и в двух способах задания интегральной модели ограничений:
1. Без интегральных ограничений.
2. Интегральные ограничения равны текущему интегральному значению приемистости (задача перераспределения).
Результаты расчетов сведены в таблицу 1.
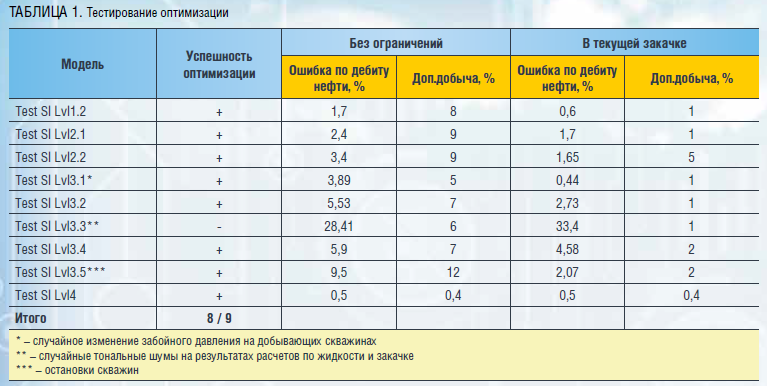
Инструмент справляется с оптимизацией в 8 из 9 сценариев, однако в сценарии с тональными шумами (Test SI Lvl 3.3) значительно ошибается в добыче нефти.
Тестирование на реальном месторождении
Для тестирования реализованных алгоритмов на фактических данных выбрано одно из месторождений Западной Сибири, которое характеризуется небольшим фондом действующих добывающих скважин (28 ед.) и отсутствием за последние 1,5 года тяжелых ГТМ (ГРП, ЗБС). На рисунке 9 представлены результаты обучения на фактических суточных данных.
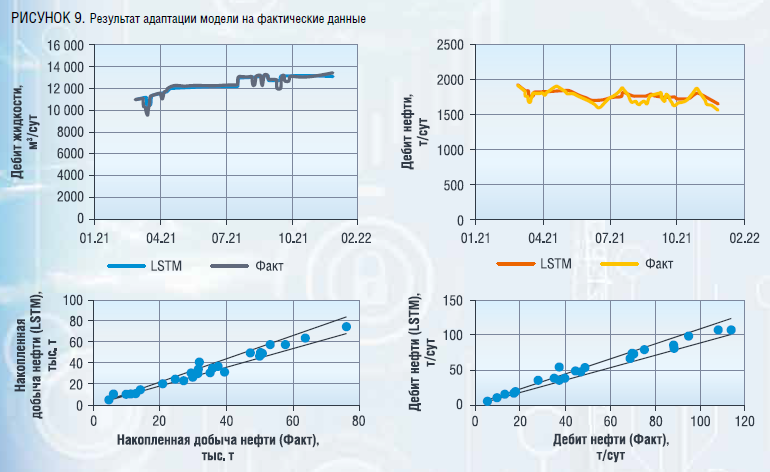
Адаптация модели удовлетворительная: ретроспективный прогноз по 83 % добывающих скважин находится в диапазоне 10 %.
На обученных моделях была рассчитана оптимизационная задача в двух сценариях:
1. Без интегральных ограничений.
2. Интегральные ограничения равны текущему значению суммарной приемистости.
Оптимальные режимы, полученные при расчете в инструменте, подставлены в адаптированную ГДМ модель. Полученные на ГДМ потенциалы от регулирования закачки сведены в таблицу 2.

Применение инструмента позволило оптимизировать закачку для достижения дополнительной добычи нефти, как в условиях ограниченной интегральной закачки, так и в случае неограниченного роста интегральной закачки.
Заключение
Разработан прототип инструмента, основанный на нейросетевых технологиях, который позволяет рассчитывать оптимальные режимы работы нагнетательных скважин. В разработанном инструменте используется авторская методика обработки промысловых данных с применением технологий машинного обучения, а также в расчетном ядре модели LSTM применены модификации, позволяющие на качественном уровне учитывать физику процесса фильтрации.
На текущий момент инструмент протестирован на синтетических данных. Оптимальные режимы, полученные при расчете, подставлены в адаптированную гидродинамическую модель и выполнен прогноз двух вариантов: базового – без изменения режимов нагнетания, оптимизированного – изменение режимов нагнетания согласно инструменту. По результатам расчетов дополнительная добыча нефти прогнозируется как в условиях ограниченной интегральной закачки, так и в случае неограниченного роста закачки.
Дальнейшее развитие инструмента связано:
· Моделирование фильтрации двухфазного потока с применением методики физико-информированных нейронных сетей.
· Тестирование прототипа на большем количестве скважин и на различных месторождениях с целью определения границ применимости нейросетевых технологий при процессах регулировании закачки.
Литература
1. Бриллиант Л.С., Горбунова Д.В., Завьялов А.С., Симаков Е.А., Бескурский В.В., Рябец Д.А. «Управление добычей на основе нейросетевой оптимизации режимов работы скважин на объекте БС8 Западно-Малобалыкского месторождения» // «Neftegaz.RU» – 2019. – № 6.
2. Бриллиант Л.С., Завьялов А.С., Данько М.Ю., Елишева А.О., Цинкевич О.В. «Методика тестирования алгоритмов прокси-моделирования» // Недропользование – ХХI век. – 2020. – № 4. – С. 128–137.
3. Бриллиант Л.С., Комягин А.И., Бляшук М.М., Цинкевич О.В., Журавлёва А.А. Патент «Способ оперативного управления заводнением пластов» // RU 2614338 C1.
4. Вершинин В.Е., Пономарев Р.Ю. «Long-Term Forecasting and Optimization of Non-Stationary Well Operation Modes Through Neural Networks Simulation» // SPE – 206529-MS.
5. Вершинин В.Е., Пономарев Р.Ю., Стрекалов А.В., «Neural Network as a Tool for Predicting and Controlling the Technological Regime of Production Wells» // SPE – 201937-MS.
6. Иваненко Б.П., «Нейросетевое имитационное моделирование нефтяных месторождений и гидрогеологических объектов» // Томск: Издательский Дом ТГУ, 2014. – 188 с.
7. Колмогоров А.Н. О представлении непрерывных функций нескольких переменных в виде суперпозиции непрерывных функций одного переменного. Доклад. АН СССР, 1957, т. 114, № 5, с. 953–956.
8. Потрясов А.А, Бриллиант Л.С., Печеркин М.Ф., Комягин А.И. «Автоматизация процессов управления заводнения на нефтяном месторождении» // Недропользование – ХХI век. – 2016. – № 6. – С. 114–123.
9. Ручкин А.А. Исследование особенностей оценки взаимовлияния скважин на примере модели CRM / А.А. Ручкин, С.В. Степанов, А.В. Князев, А.В. Степанов, А.В. Корытов, И.Н. Авсянко // Вестник Тюменского государственного университета. Физико-математическое моделирование. Нефть, газ, энергетика. 2018. Том 4. № 4. С. 148–168. DOI: 10.21684/2411-7978-2018-4-4-148-168.
10. Степанов С.В. Проблематика оценки взаимовлияния добывающих и нагнетательных скважин на основе математического моделирования / С.В. Степанов, С.В. Соколов, А.А. Ручкин, А.В. Степанов, А.В. Князев, А.В. Корытов // Вестник Тюменского государственного университета. Физико-математическое моделирование. Нефть, газ, энергетика. 2018. Том 4. № 3. С. 146–164. DOI: 10.21684/241-1-7978-2018-4-3-146-164.
11. Стрекалов А.В., Хусаинов А.Т. «Математическое моделирование процессов нефтедобычи на основе нейронных сетей» // ТюмГНУ. 2013.
12. De Berg M. Van Kreveld M. Computational Geometry. Algorithms and Applications. Second, Revised Edition. Berlin: Springer-Verlag. – 2000. – P. 367.
13. Development of an artificial neural network model for prediction of bubble point pressure of crude oils. Southwest Petroleum University. 2018.
14. Emre Artun, Characterizing Reservoir Connectivity and Forecasting Waterflood Performance Using Data-Driven and Reduced-Physics Models // SPE -180488-MS. 2016.
15. S. G. Ponnambalam, N. Jawahar, P. Aravindan A simulated annealing algorithm for job shop scheduling, Production Planning & Control: The Management of Operations, 10:8, 1999 г., с. 767–777.