Ключевые слова: октановое число бензина, инфракрасная спектрометрия, машинное обучение, сокращение признакового пространства, Lasso-регрессия, метод опорных векторов.
Неинвазивные по своей природе оптические методы исследования углеводородных систем широко применяют для мониторинга свойств газовых и жидких сред в нефтегазовой промышленности. Эти высокочувствительные методы удобны для организации процесса измерений, что важно как при проведении лабораторных анализов, так и для контроля технологических процессов. Наибольшее распространение получила колебательная спектроскопия в инфракрасном (ИК) диапазоне, прежде всего за счет высокой информативности колебательных спектров углеводородов и возможности соотнесения полос поглощения с характерными химическими связями соединений, входящих в состав бензина, в средней ИК-области. Для онлайн-мониторинга предпочтительно применение методов ближней ИК-спектроскопии ввиду возможности передачи оптического сигнала без потери его интенсивности по оптоволокну на большие расстояния внутри предприятия.
За последние годы было опубликовано более 100 работ по предсказанию свойств различных топлив (бензинов и дизельных топлив) на основе спектральных данных с использованием методов хемометрики. Математические модели предложены для предсказания более 50 различных показателей на основании данных различных спектральных методов [1–3]. В числе предсказываемых свойств – вязкость, плотность, теплота сгорания, содержание влаги, серы и азота, температура вспышки, холодные свойства, фракционный состав и др. Многие из этих работ имеют лишь академический интерес, поскольку изученные моделируемые показатели относительно легко можно измерить напрямую. Наибольший интерес для предсказания по данным косвенных методов имеют показатели, прямое измерение которых связано с высокими затратами времени и ресурсов. К таким показателям относятся октановое число бензинов (ОЧ) и цетановое число для дизельных топлив.
В данной статье рассматриваются возможности предсказания ОЧ для одного из наиболее изученного объекта хемометрического анализа в нефтяной практике НПЗ – бензина. ОЧ определяет детонационную стойкость бензина (именно ее величиной маркируют нефтепродукт на АЗС), при этом для определения ОЧ требуется больше всего ресурсов по сравнению с другими методами контроля эксплуатационных свойств нефтепродуктов. Интерес исследователей к поиску адекватных математических предсказательных моделей ОЧ не ослабевает [8, 14, 15]. Оценка значения ОЧ моторным методом проводится путем измерений на реальном моторном стендовом двигателе сравнением детонационных характеристик исследуемого образца бензина с эталонными топливами на основе эталонных смесей углеводородов: н-гептана и изооктана, или н-гептана, изооктана и толуола.
Набор используемых данных
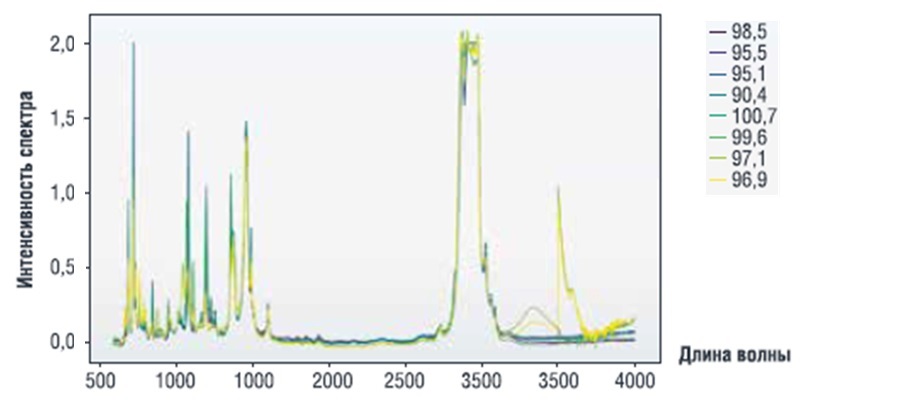
Собранные данные включают в себя результаты спектрального анализа 512 образцов бензинов, для которых в результате лабораторных экспериментов были определены октановые числа. Примеры изменения интенсивности излучения в зависимости от длины волны для некоторых образцов бензинов из рассматриваемого набора данных приведены на рис. 1.
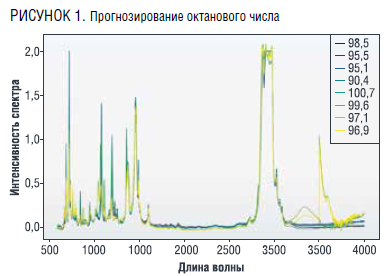
Эксперименты были проведены в 10 различных лабораториях, частоты спектров варьировались от 600 по 4000 с шагом 0,5. Таким образом, для каждого образца бензина имеется спектр интенсивностей, соответствующих указанным длинам волн, включающий 6802 значения. Октановые числа бензинов в рассматриваемом наборе данных находятся в интервале от 90,4 до 102. При этом было только одно значение ниже 91,5; 120 значений в интервале от 91,5 до 92,5; 158 значений в интервале от 94,5 до 95,5; 22 значения в интервале от 97,5 до 98,5 и 62 значения превышают 98,5. Целью работы было разработать модель на основе методов машинного обучения для определения октанового числа по данным спектрального анализа.
Математическая постановка задачи
Для применения методов машинного обучения будем рассматривать результаты спектрального анализа для каждого образца бензина и его октановое число, определенное в лабораторных условиях, как обучающую выборку:
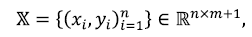
Где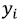 
– октановое число для i-го образца бензина, n - количество образцов бензинов в обучающей выборке, m - количество признаков, то есть длин волн в спектре, для которых определена интенсивность излучения.
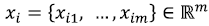
набор значений интенсивностей длин волн (вектор размерности m).
Задача состоит в построении модели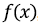 
, параметры которой подбираются по имеющейся обучающей выборке так, чтобы рассогласование между получаемыми расчетными значениями 
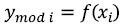и известными из лабораторных экспериментов значениями октановых чисел 
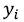было наименьшим. В качестве критерия, который определяет, насколько согласуются расчетные и известные значения целевой переменной (октанового числа в нашем случае), обычно используют среднеквадратическое отклонение:
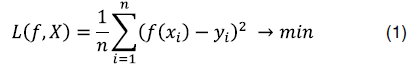
Таким образом, «обученная» на собранных данных обучающей выборки модель по поданному на вход набору признаков х (интенсивности спектра) сможет предсказать значение октанового числа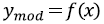 
для любого образца бензина.
Способы сокращения числа признаков
Следует отметить, что данные имеют избыточно много признаков (6802) при том, что самих образцов всего 512. Это может привести к целому ряду проблем:
* Переобучение – при использовании всех доступных признаков необходимо вводить большое число параметров модели, при этом для некоторых методов машинного обучения задача может оказаться некорректной (не иметь единственного решения) или же параметры будут вычислены так, чтобы максимально настроиться именно на данные обучающей выборки, при этом модель может потерять обобщающую способность, то есть на данных, не попавших в обучающую выборку, предсказанное значение не будет иметь желаемую точность.
* Проклятие размерности. С увеличением числа признаков пространство, в котором они существуют, становится разреженным. Это усложняет задачу поиска закономерностей между признаками и целевой переменной, так как для надежной оценки параметров требуется экспоненциально больше данных.
* Высокая вычислительная сложность. Большое количество признаков требует больше ресурсов для обработки и анализа данных, что может значительно увеличить время обучения моделей и затраты на вычислительные ресурсы.
В связи с этим возникает дополнительная задача о сокращении размерности признакового пространства [5, 10, 11, 16, 17]. Эта задача может решаться как с помощью отбора наиболее информативных признаков, так и путем формирования вторичных входных признаков, которые могут быть результатом различных комбинаций исходных признаков [9]. Оба этих подхода были опробованы в процессе работы над задачей.
LASSO-регрессия широко применяется для отбора признаков [12]. Изначально идея регуляризации (то есть контроля за величиной коэффициентов регрессии) возникла при преодолении проблемы мультиколлинеарности (наличие сильной линейной зависимости между некоторыми признаками) при построении классических моделей множественной линейной регрессии. При использовании LASSO-регрессии вводится дополнительный множитель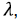 
который отвечает за штраф при больших по модулю значениях коэффициентов регрессии:
Особенностью данного метода является то, что в качестве входных данных модели могут быть включены линейно зависимые или незначимые признаки, при этом если k-й признак незначим, коэффициент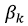 
примет значение 0. При использовании LASSO-регрессии величина вычисленных коэффициентов будет пропорциональна важности соответствующих признаков в случае линейной (или монотонной) зависимости между признаком и целевой переменной. Для рассматриваемой задачи было определено лучшее значение параметра 
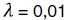, при этом ненулевые значения коэффициентов получили 97 признаков (длин волн спектра).
В качестве метрики для сравнения качества моделей, полученных с помощью разных методов машинного обучения, будем использовать квадратный корень из среднеквадратического отклонения:
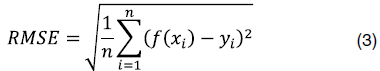
Для полученной модели LASSO-регрессии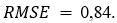 
Значение ошибки достаточно велико, поэтому мы не будем рассматривать этот метод в качестве модели для предсказания, а воспользуемся его результатами именно для сокращения набора исходных признаков и построим модели, используя другие алгоритмы машинного обучения.
Популярный алгоритм машинного обучения случайный лес (RF – Random Forest [4]) в процессе построения модели производит формирование ансамбля деревьев решений. При построении дерева решений в каждой вершине происходит разбиение множества всех значений выборки на два подмножества, для этого выбирается признак и его пороговое значение так, чтобы сумма среднеквадратичной ошибки для каждой части выборки в узлах, полученных после разбиения, была наименьшей:
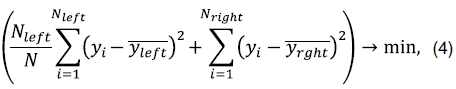
где N – число объектов в вершине верхнего уровня (родительской),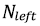 
– число объектов в левой вершине (при значении признака меньше порогового) , 
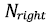– число объектов в правой вершине (при значении признака больше порогового).
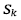(и, соответственно, разбиения по признаку 
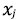) можно вычислить сокращение среднеквадратичной ошибки:
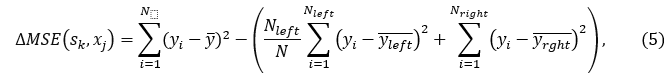
В процессе построения решающего дерева один и тот же признак может выбираться несколько раз, таким образом, информативность (важность) признака определяется тем, насколько при выборе этого признака сократилась среднеквадратичная ошибка:
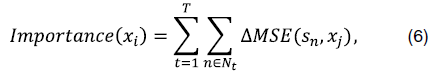
где
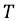– число деревьев в случайном лесу, 
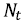- множество узлов в дереве t, которые используют признак xj для разделения.На рис. 2 показаны 20 наиболее информативных признаков, отобранных с помощью случайного леса. Всего для дальнейшего анализа было отобрано 153 признака. Преимуществом алгоритма случайного леса является то, что он успешно воспроизводит нелинейные зависимости и достаточно устойчив к переобучению.
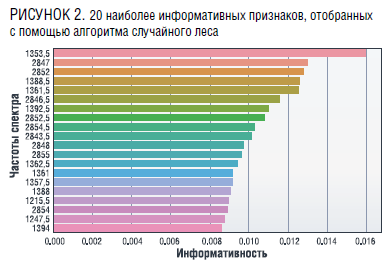
Метод главных компонент – популярный способ понижения размерности данных. Он основан на вычислении собственных векторов и собственных значений ковариационной матрицы исходных данных и позволяет получить новые признаковые переменные в виде линейной комбинации исходных признаков так, чтобы новые переменные определяли ортогональные вектора, в направлении которых дисперсия данных будет максимальной. То есть можно построить отображение исходного признакового пространства в новое и взять меньшее число признаков (главных компонент), при этом сохранится максимум информации об объектах (будет отражено 95–99 % дисперсии всех данных). На рис. 3 показано, что для исследуемого набора данных можно использовать 20 главных компонент (новых признаков), при этом они будет объяснять 99 % дисперсии всех данных. Таким образом, был получен новый набор признаков, для которого можно построить модели с помощью различных алгоритмов машинного обучения.
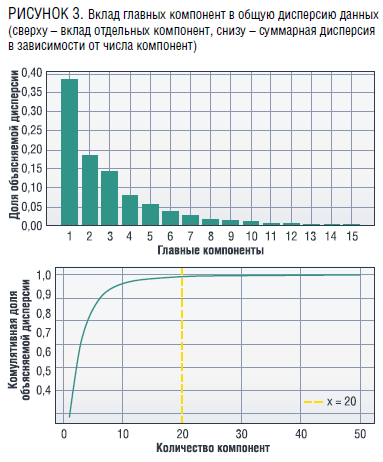
В качестве альтернативы методу главных компонент в [13] был предложен метод, который более предпочтителен для работы с данными, имеющими нелинейные связи, t-SNE стохастическое вложение соседей с распределением Стьюдента – (t-Distributed Stochastic Neighbor Embedding). Этот метод основан на расчете условных вероятностей сходства объектов в исходном пространстве, в результате t-SNE может быть получено распределение вероятностей в новом пространстве меньшей размерности, при этом объекты, которые были близки в исходном пространстве, имеют высокие вероятности быть близкими и в новом пространстве. То есть в случае успешного применения этого метода можно визуализировать многомерные данные в двух- и трехмерном пространстве, при этом будут выделены достаточно обособленные группы объектов. На рис. 4 показано полученное распределение для двухмерного пространства: каждая точка на плоскости – образец бензина, цветом показано октановое число, определенное для этого образца. Из рис. 4 видно, что некоторые группы достаточно четко выделены и цвет (значение октанового числа) внутри них стабилен, в то же время есть достаточно большие области, где октановые числа сильно отличаются. В процессе анализа были выбраны значения гиперпараметров метода: число компонент – 8, параметр перплексия – 10.
Сравнение моделей
В нашем исследовании были построены модели при использовании метода опорных векторов (SVM [Cortes]), случайного леса (Random Forest, RF), метода k ближайших соседей (KNN) и метода градиентного бустинга (GB). Для корректной оценки качества полученных моделей весь доступный объем данных необходимо разбить на три части – обучающую, валидационную и тестовую выборки. Валидационная выборка необходима для того, чтобы подобрать гиперпараметры для каждого метода. В таблице 1 приведены метрики моделей (RMSE), полученные для всех описанных выше способов сокращения признакового пространства для тестовой выборки. Из таблицы 1 следует, что метод опорных векторов показал наилучшие результаты для всех полученных вариантов сокращенного набора признаков. В качестве ядра для модели метода опорных векторов были использованы радиальные базисные функции. Среди рассмотренных методов отбора признаков для всех моделей лучшие результаты были получены после применения LASSO-регрессии.
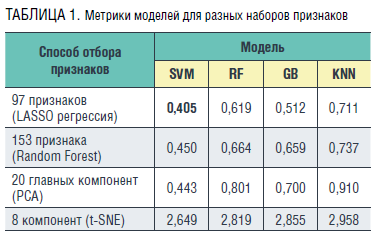
Поскольку данные для работы были собраны из разных источников, возник вопрос о том, насколько они согласованы: хотелось исключить ситуацию, когда значения октанового числа, полученные в какой-либо лаборатории, имеют систематическую ошибку и резко отличаются от данных остальных лабораторий. Для этого был построен график, показанный на рис. 4, где значения, полученные в каждой лаборатории, показаны разным цветом. На графике сопоставлены реальные и вычисленные с помощью построенной модели октановые числа. Из графика видно, что точки хорошо сгруппированы около диагонали (то есть расчетные и фактические значения хорошо согласуются между собой), для различных значений октанового числа разброс примерно одинаковый. Есть несколько отдельных замеров, отклоняющихся от линии, при этом в отклонениях нет преобладания одного цвета (данных одной лаборатории), поэтому можно считать результаты, полученные из разных лабораторий, достаточно согласованными.
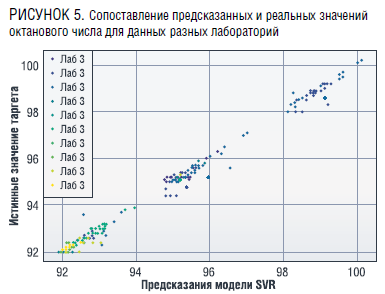
Построенная на рис. 6 кривая регрессионных ошибок (REC-кривая [7]) показывает, что для 85 % данных тестовой выборки абсолютная ошибка при определении октанового числа не превышает 0,5 и всего для четырех образцов бензина она превосходит 1.
При этом медианное значение ошибки составляет 0,25. Коэффициент детерминации модели, рассчитанный для всего объема данных, R2 = 0,94.
Заключение
В работе представлены результаты решения задачи построения модели на основе методов машинного обучения для определения октанового числа по данным спектрального анализа. Особенностью этой задачи является большое число признаков, поэтому рассмотрены различные способы сокращения признакового пространства. Среди методов уменьшения размерности лучшие результаты были получены отбором признаков с помощью построения Lasso-регрессии и понижением размерности методом PCA. В нашем исследовании были построены модели при использовании метода опорных векторов, случайного леса, метода k ближайших соседей и метода градиентного бустинга. Наилучшие результаты были получены с помощью применения метода опорных векторов с ядром на основе радиальных базисных функций. Тестирование модели показало, что для 85 % данных тестовой выборки абсолютная ошибка при определении октанового числа не превышает 0,5, коэффициент детерминации модели R2 = 0,94.
Литература
1. Baird Z.S., Oja V. Predicting fuel properties using chemometrics: a review and an extension to temperature dependent physical properties by using infrared spectroscopy to predict density / Chemometrics and Intelligent Laboratory Systems. – 2016 – № 158, P. 41–47. – doi: 10.1016/j.chemolab.2016.08.004.
2. Balabin, R.M. Gasoline classification by source and type based on near infrared (NIR) spectroscopy data / R.M. Balabin, R.Z. Safieva / Fuel. – 2008. – Vol. 87, № 7. – P. 1096–1101. – DOI 10.1016/j.fuel.2007.07.018.
3. Balabin, R.M. Gasoline classification using near infrared (NIR) spectroscopy data: Comparison of multivariate techniques / R.M. Balabin, R.Z. Safieva, E.I. Lomakina / Analytica Chimica Acta. – 2010. – Vol. 671, № 1–2. – P. 27–35. – DOI 10.1016/j.aca.2010.05.013. – EDN MXFGWL.
4. Breiman L. Random forests //Machine learning. – 2001. – Т. 45. – № 1. – С. 5–32.
5. Chen RC., Dewi, C., Huang, SW. et al. Selecting critical features for data classification based on machine learning methods. J Big Data 7, 52 (2020). https://doi.org/10.1186/s40537-020-00327-4.
6. Cortes C., Vapnik, V. Support-vector networks / Machine Learning. – 1995. – № 20, p. 273– 297, DOI: 10.1007/BF00994018.
7. Jinbo Bi, Bennett K.P. Regression Error Characteristic Curves / Proc. of the 20th Int. Conf. on Machine Learning (ICML-2003), Aug. 21–24, 2003, Washington, DC, USA. – 2003. – P. 43–50.
8. Kelly J.J., Barlow C.H., Jinguji T.M., Callis J.B. Prediction of gasoline Octane Numbers from Near-Infrared Spectral Feature in the Range 660-1215 nm // Analytical Chemistry. – 1989. – V.61. № 4, p. 313–320.
9. Kochueva O.N. Feature Selection for a Fuzzy Classification Model Based on a Genetic Algorithm / Распределенные компьютерные и телекоммуникационные сети: управление, вычисление, связь (DCCN-2022) = Distributed computer and communication networks: control, computation, communications (DCCN-2022): Материалы XXV Международной научной конференции, Москва, 26–30 сентября 2022 года. – Москва: Российский университет дружбы народов (РУДН), 2022. – P. 168–175. – EDN PSBIGK.
10. Ladha L., Deepa T. Feature selection methods and algorithms /International journal on computer science and engineering. – 2011. – V. 3. – № 5. – P. 1787–1797.
11. Sorzano C. O. S., Vargas,A. Pascual Montano A survey of dimensionality reduction techniques / arXiv. – 2014. – 1403.2877, https://doi.org/10.48550/arXiv.1403.2877.
12. Tibshirani R. Regression shrinkage and selection via the lasso /Journal of the Royal Statistical Society. Series B (Methodological). – 1996. – V. 58, p. 267–288.
13. Van der Maaten L., Hinton G. Visualizing High Dimensional Data Using t-SNE / Journal of Machine Learning Research. –2008. – V. 9, P. 2579-2605.
14. Об особенностях и эффективности применения абсорбционной оптической спектроскопии в контроле технологического процесса производства высокооктановых бензинов / Н.И. Егорова, И.О. Конюшенко, В.М. Немец [и др.] // Вестник Тюменского государственного университета. Физико-математическое моделирование. Нефть, газ, энергетика. – 2018. – Т. 4, № 2 – С. 120–135. – DOI 10.21684/2411-7978-2018-4-2-120-135. – EDN USMWSY.
15. Разработка и валидация многомерных моделей для определения октанового числа первичных эталонных топлив / Р.Г. Романова, Р.А. Кулиева, А.В. Семенов, Д.А. Мифтахутдинов / Вестник Технологического университета. – 2020. – Т. 23, № 4. – С. 64–67. – EDN GJXYFL.
16. Киселева, В.А. Отбор признаков в машинном обучении / В.А. Киселева, А.А. Кузин, П.Д. Шульпина / Телекоммуникации и информационные технологии. – 2023. – Т. 10, № 2. – С. 21–29. – EDN RQIDYJ.
17. Методика выбора входных признаков для алгоритмов машинного обучения / В.В. Тагунов, К.Я. Кудрявцев, А.И. Петрова, Т.И. Возненко / Вестник Национального исследовательского ядерного университета «МИФИ». – 2022. – Т. 11, № 1. – С. 51–58. – DOI 10.56304/S2304487X22010114.
