Многофазные потоки играют важную роль во многих промышленных и технических системах, особенно в нефтегазовой отрасли. Они возникают при транспортировке нефти, газа, воды и других многофазных смесей по насосно-компрессорным трубам нефтяной скважины. Понимание поведения и классификация двухфазного потока в вертикальных трубопроводах имеют огромное значение для оптимизации процессов транспортировки водонефтяной смеси.
Цель данной научной статьи состоит в исследовании и разработке метода моделирования и классификации двухфазного потока в вертикальном трубопроводе с использованием численного моделирования и нейронных сетей. Подход сочетает в себе преимущества численного моделирования и нейронных сетей для достижения более точного и эффективного предсказания поведения двухфазных потоков. В работе применяется широко используемый инструмент численного моделирования – OpenFOAM. Он обеспечивает высокую точность в описании физических процессов двухфазного потока, таких как давление, распределение фаз и изменение состояния потока. Однако даже с использованием точной модели классификация типов двухфазного потока остается сложной задачей. Затем применяется подход использования для решения задания классификации типов двухфазного потока с использованием нейронных сетей. Для обучения модели искусственной нейронной сети использовались изображения с результатов компьютерного моделирования поведения двухфазного потока. Модель данных состояла из более 25 тысяч изображений из 30 численных расчетов. Обучение нейронной сети на большом объеме данных позволяет достичь высокой точности классификации и обеспечить устойчивость к различным условиям эксплуатации скважины.
Полученные результаты сопоставляются с известными картами течения двухфазного потока в вертикальном трубопроводе для оценки точности определения типа течения водонефтяной смеси.
Объект и методы исследования
Особенности потока
В качестве исследуемого потока выступает водонефтяная смесь при различных значениях обводненности. Плотность смеси изменятся от 87 до 1039 кг/м3 . В расчетах, согласно ГОСТ Р 51858–2002 «Нефть. Общие технические условия», была использована легкая нефть с плотностью 850 кг/м3, динамическая вязкость которой составляет 25,5 сПз, при стандартных условиях [1, 2].
Постановка задачи
Целью данного исследования является моделирование и классификация двухфазного потока в вертикальном трубопроводе с использованием численного моделирования и нейронных сетей.
Для достижения поставленной цели необходимо решить ряд задач:
- Моделирование потока водонефтяной смеси в насосно-компрессорной трубе скважины. Результаты моделирования в дальнейшем будут использоваться в качестве обучающей и тестовой выборки.
- Обучение и настройка искусственной нейронной сети под решение задачи мультиклассовой классификации.
- Сопоставление результатов классификации обученной нейронной сети с уже имеющимся картами течения двухфазного потока в вертикальных трубопроводах.
В качестве визуализации двухфазного потока применяется подход компьютерного моделирования в программном продукте OpenFOAM. Выбор программного обеспечения состоит в следующем: открытость исходного кода, инструментальная гибкость и разнообразие моделей турбулентности. В качестве анализируемого потока использовалась водонефтяная смесь, свойства которых были описаны ранее.
Расчетная область представлена вертикальным участком насосно-компрессорной трубы (далее НКТ) с диаметром 82 мм. Длина участка НКТ составляет десять метров. Разбиение геометрической модели осуществлялось комбинацией гексаэдрических и призматических типов ячеек. Общее количество ячеек составляет 238 400 элементов, среди которых 89,3 % составляют гексаэдры. Средняя длина грани ячейки составляет ~14 мм, для наблюдения взаимодействия между собой фаз.
Поперечное сечение насосно-компрессорной трубы представлено на рисунке 1.
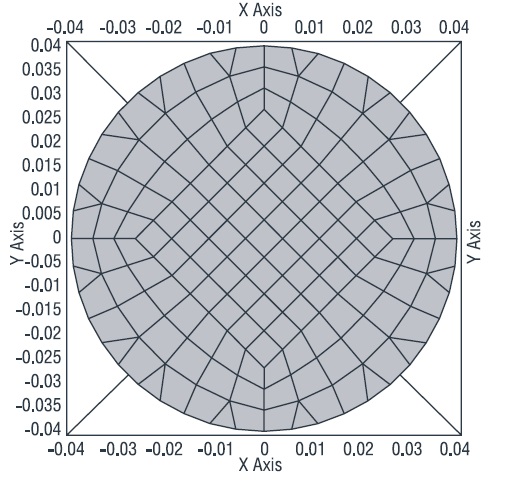
Рисунок 1. Поперечное сечение расчетной области
Расчеты выполняются с вариацией объемных содержаний фаз и скоростей потока, для того чтобы наблюдать переходы в различные области типов течения двухфазного потока. Диапазон изменения скоростей от 1 м/c до 11 м/c с шагом 2 м/c, диапазон изменения объемного содержания фаз от 0,1 до 0,9 с шагом 0,2 дольных единиц. Для расчета был использован решатель InterFoam. В конечном итоге для создания набора данных, которые впоследствии будут использоваться для работы ИНС, составляют 30 численных расчетов [3].
Граничное условие на входе в расчетную область – постоянное значение скорости, а на выходе – условие свободного протекания. На стенках - условие прилипания для скорости.
В данной работе использовался двухфазный подход для моделирования движения газожидкостной смеси в трубе. Все расчеты воспроизводились в нестационарном двухфазном решателе InterFOAM в платформе для численного моделирования OpenFOAM. Такой решатель предназначен для двух несжимаемых изотермических несмешивающихся фаз с использованием VOF-метода.
Сам решатель InterFOAM представляет собой решатель для двух несжимаемых фаз. Все расчеты производятся на основе двух уравнений уравнения импульса и неразрывности:
Формула 1
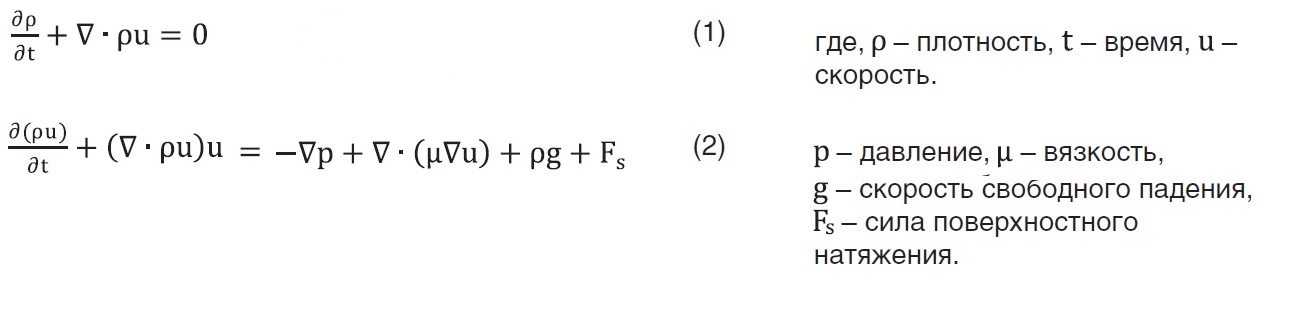
В данном решателе присутствует переменная для определения значения которой решается третье уравнение переноса объемной доли:
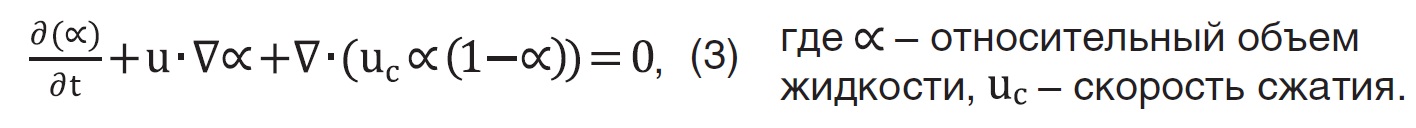
С помощью нее будет поддерживаться четкая граница раздела между двумя фазами.
В этом уравнении œ это доля одной фазы в данной фазе и других фаз. Значение будет рассчитываться автоматически.
В основе метода лежит идея введения переменной относительного объема жидкости , которая содержится в ячейке. В случае когда œ, жидкость полностью занимает ячейку, когда œ то ее занимает газовая фаза, если не рассматривается газ, то ячейку занимает вакуум. Когда œ, то ячейка содержит свободную поверхность.
Значения других переменных, которые участвуют при моделировании процесса будет рассчитываться непосредственно в процессе самого моделирования.
Так, скорость, плотность вязкость, средневзвешенная скорость рассчитываются при помощи следующих формул:
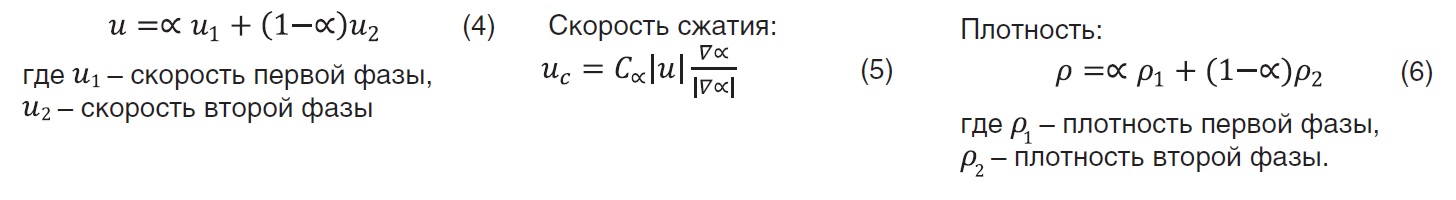
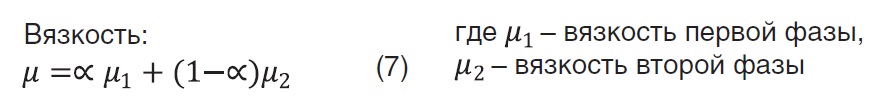
Карты режимов течения
Для первоначальной оценки режима течения использовались карты режимов течения. В работе использовалась карта Азиза.
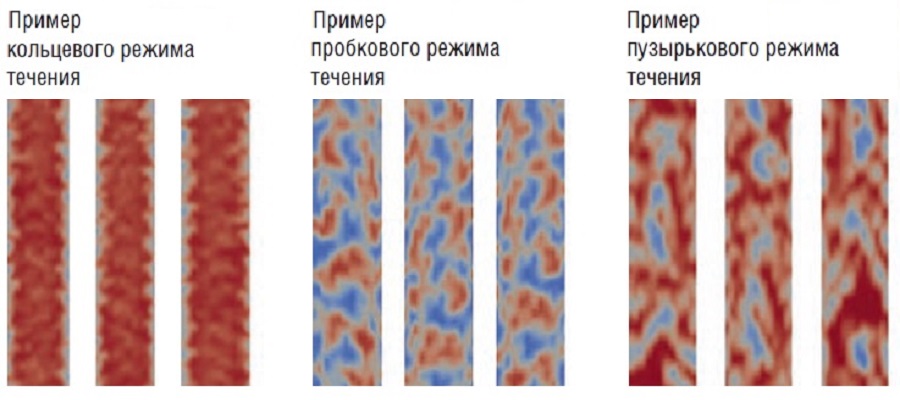
Данная диаграмма предназначена для вертикальных каналов. В ней присутствуют пузырьковый, пробковый, переходной и кольцевой/эмульсионный режимы.
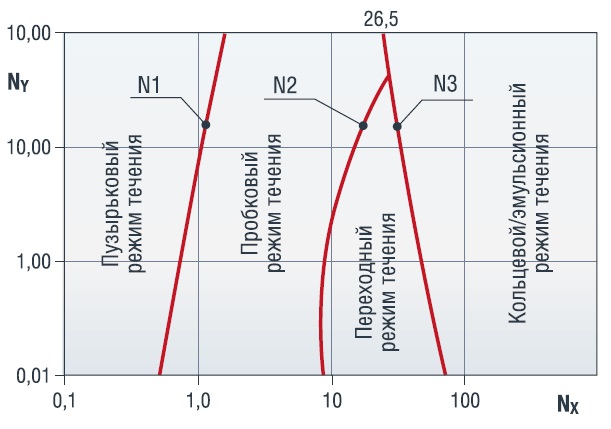
Рисунок 2. Диаграмма Азиза для многофазных потоков вертикальных труб
Такая диаграмма тоже качественно определяет тип течения. Для работы с ней вычисляются следующие параметры:

Далее будет описан алгоритм классификации типа течения многофазной смеси. Для каждого расчетного шага вычисляются значения, после этого ставят точку на диаграмму и определяется режим течения.
Границы между режимами определяются следующими параметрами:

В работе получилось воссоздать с помощью численного моделирования три режима течения: пузырьковый, пробковый, кольцевой.
Сверточная нейронная сеть
В данном исследовании использовались сверточные нейронные сети (СНС). Рассмотрим, как они работают и как происходит их обучение. Далее на изображении будет показан пример работы сверточной нейронной сети (рисунок 3). Для лучшего понимания СНС разберем их режим работы.
Возьмем изображение размером n×nn \times nn×n пикселей, где каждый пиксель содержит три значения (RGB). Первый слой СНС всегда является сверточным. Применяется сверточная матрица, также известная как фильтр или ядро, например, размером 5∙5, и выполняется поэлементное умножение. В результате получается матрица размером (n-4) ∙ (n-4) ∙3.3.
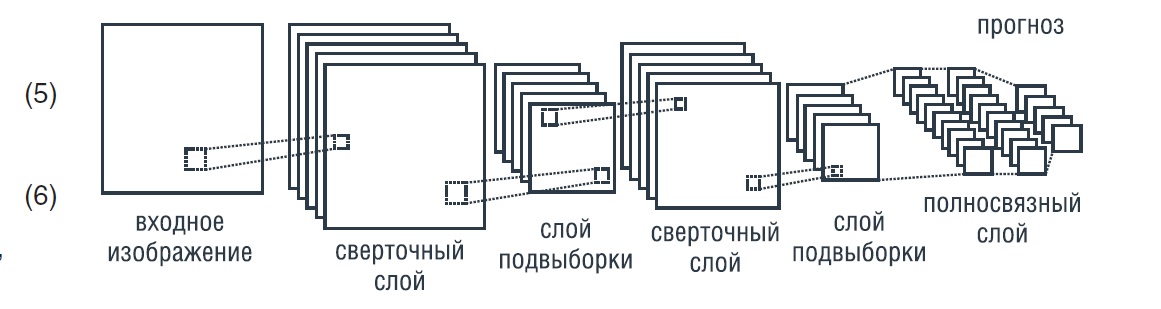
Рисунок 3. Пример работы сверточной нейронной сети
После прохождения через первый сверточный слой выходные значения становятся входными для следующего слоя, и этот процесс повторяется несколько раз. Важно отметить, что чем больше слоев, тем более сложные образы может распознавать сеть.
Теперь рассмотрим, зачем в конце нейронной сети нужен полносвязный слой. Он необходим для определения высокоуровневых признаков на основе входных изображений и числа классов K. В данном исследовании, например, при численном моделировании K = 3 (пузырьковый, эмульсионный, кольцевой режимы течения).
Разберем, как работает полносвязный слой на примере данных, использованных в исследовании. Например, если модель определяла пузырьковый режим течения, то активировались карты свойств, соответствующие этому режиму, а для других режимов активировались карты, соответствующие этим режимам [4, 5].
РИСУНОК 4. Данные, поступающие в нейронную сеть для обучения

Результаты и обсуждения
Результаты моделирования
Ниже представлены результаты численного моделирования
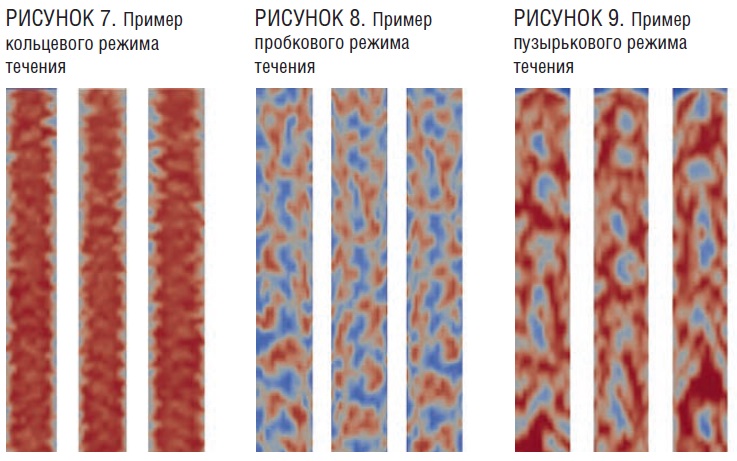
Каждый режим течения был представлен 20 идентичными изображениями (см. рисунки 7, 8, 9). Эти изображения загружались в дополнительное программное обеспечение, разработанное на языке Python. В данном программном модуле изображения распределялись по трем папкам, соответствующим обучающей, проверочной и тестовой выборкам. Далее случайным образом исключались некоторые изображения, которые впоследствии использовались для верификации. Результаты этой верификации будут показаны после графиков истории обучения.
Изображения, поступающие в нейронную сеть для дальнейшей обработки, имели разрешение 100x100 пикселей.
Таким образом, для обучения использовалось 20000 изображений потоковых режимов многофазной среды. Для проверки было выделено 5000 изображений, а для тестирования — 5000 изображений. Около 200 изображений были отведены для верификации режима потока. Эти изображения анализировались с помощью отдельного программного обеспечения после завершения обучения и сохранения весов нейронной сети. Процесс верификации выглядел следующим образом: изображение загружалось в уже обученную сеть, которая в режиме реального времени определяла режим потока на изображении [6, 7].
Результаты качества обучения нейронной сети
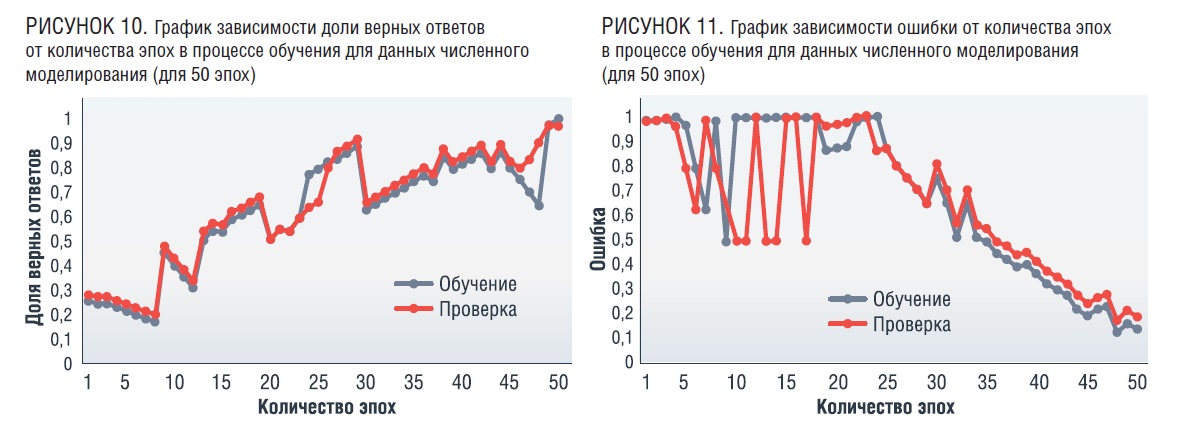
Для обучения были проведены несколько итераций количества эпох обучения. 25, 50, 75, 100 эпох. Лучшая точность была достигнута при использовании 50 эпох обучения и составляет 93 % на данных, полученных с помощью численного моделирования. Ниже представлены графики зависимости доли верных ответов от количества эпох и зависимости ошибки от количества эпох в процессе обучения [8].
Результаты исследования
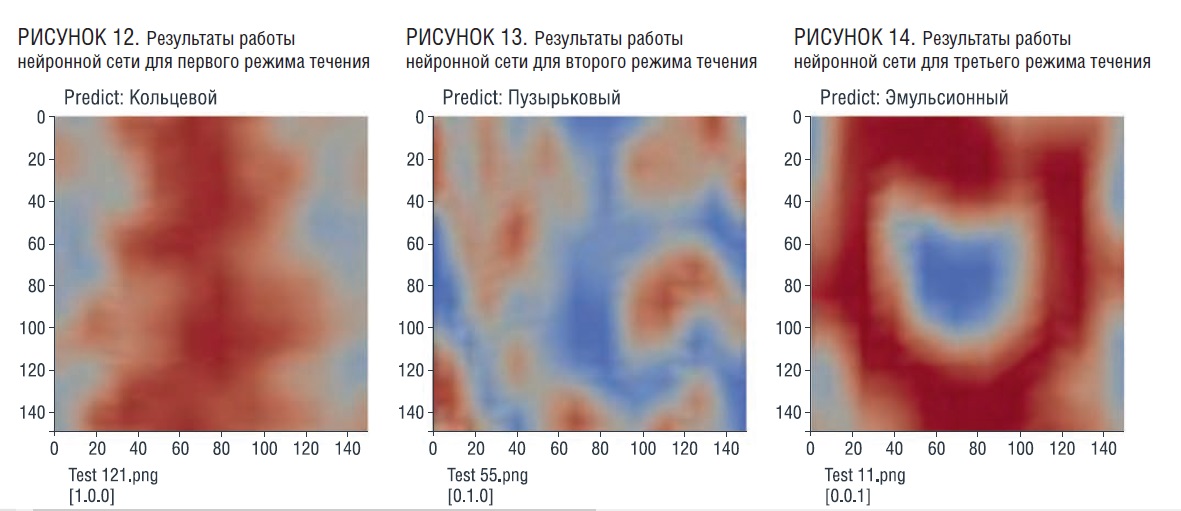
По итогам обучения нейронная сеть может классифицировать каждый режим течения, полученный при численном моделировании. Также, как и при работе с данными численного моделирования, вверху будет определяемый режим течения, а снизу – значения массива, соответствующего данному типу потока. Значение массива [1.0.0.] соответствует первому режиму течения, [0.1.0.] – второму, [0.0.1] – третьему. Далее будут представлены результаты работы [9].
Выводы
Результаты исследования показывают, что разработанный подход позволяет эффективно классифицировать типы двухфазного потока в вертикальном трубопроводе. Полученные результаты сопоставлены с картами течения двухфазного потока, что подтверждает высокую точность и применимость разработанного метода. Этот подход может быть использован для оптимизации процессов в различных технических системах, где важно точно определить тип двухфазного потока.
Эта работа вносит значительный вклад в область моделирования и классификации двухфазного потока, а также демонстрирует потенциал нейронных сетей в решении подобных задач. Результаты исследования могут быть полезны для инженеров и научных работников, занимающихся проектированием и эксплуатацией технических систем, связанных с двухфазным потоком.
Предлагаемый подход имеет значительный потенциал для применения в будущем в промышленных и инженерных системах. При этом может обеспечить более точные прогнозы и предоставить операторам систем более надежные инструменты для контроля и оптимизации двухфазных потоков в вертикальных трубопроводах (мысль о продолжении статьи, раскрыть).
Литература
1. Brackbill, J. U., Douglas B. Kothe, and Charles Zemach. «A continuum method for modeling surface tension». Journal of computational physics 100.2 (1992): 335–354.
2. G. Falcone, G. Hewitt, C. Alimonti Multiphase flow metering. Developments in petroleum scienct 2009 г. 97 с.
3. Open Source CFD, Boundary Conditions – OpenFOAM-4.1, Consulting Next, 2017, 133 c.
4. Берчик Э.Д. Свойства пластовых жидкостей. Москва: Гостоптехиздат, 1960. 295 с.
5. Бузов А.А., Максимов В.М. Метод измерения расходов фаз газоконденсатной смеси в трубопроводе, Газовая промышленность. 2010. 20–21 с.
6. С.А. Вакуленко, А.А.Жихарева Практический курс по нейронным сетям. Санкт-Петербург 2018. 57 с.
7. С. Хайкин Нейронные сети полный курс. Второе издание. Москва 2006 г. 123 с.
8. Т. Ганегедара Обработка естественного языка в контексте Data Science фреймворков. ДМК Пресс 2020 г.
Ф.М. Гафаров, А.Ф. Галимянов Искусственные нейронные сети и их приложения. Издательство Казанского университета. Казань 2018 г. 85 с.