Ключевые слова: скважина, интерференция, модель, матрица, разрыв.
Решения о горизонтальном и вертикальном расположении скважин имеют решающее значение для оптимизации нефтегазовых коллекторов. Для достижения более высокой расчетной конечной добычи сокращение расстояния между скважинами, укорачивание стволов горизонтальных скважин и увеличение масштабов гидроразрывов пласта позволяют добиться эффективной добычи и снизить затраты на бурение, что, в свою очередь, обеспечивает стабильную разработку месторождений. Однако при интенсивном размещении скважин и масштабном ГРП неизбежно возникает межскважинная интерференция, которая становится серьезным препятствием для наращивания добычи [2].
В настоящее время межскважинная интерференция является одной из наиболее распространенных проблем в основных районах разработки нефтегазовых коллекторов. Как только добывающая скважина подвергается воздействию гидроразрыва соседнего пласта, ее добыча в определенной степени снижается. Основные причины, приводящие к межскважинным интерференциям, представлены на рис. 1.
В данном контексте актуализируется задача определения оптимальной стадии и расстояния между скважинами в выбранной области бурения с учетом межскважинной интерференции. Однако определение оптимальной частоты бурения скважин является сложной задачей, поскольку требует учета широкого спектра факторов, вызывающих межскважинные помехи, таких как добыча из скважин, исчерпавших свой ресурс, конструкция колонны, вертикальное расстояние, направление смещения между родительской и дочерней скважинами, а также коллекторские и геомеханические свойства.
Высоко оценивая имеющиеся на сегодняшний день труды и наработки, следует отметить, что некоторые вопросы требуют более углубленного изучения. Так, в дальнейшем развитии и обосновании нуждается метод диагностики для определения характеристик устьевого давления при взаимодействии межскважинных трещин. Кроме того, существующие математические модели для изучения многоскважинной интерференции в нефтегазовых резервуарах, как правило, очень сложны, что еще больше сдерживает прогресс исследований в этой области. Отдельного внимания заслуживают методы восстановления добычи в скважинах, подвергшихся воздействию, в зависимости от остаточной энергии пласта. Открытой остается проблема, касающаяся того, что аналитические модели не могут явно представить систему сетей гидравлических трещин, вызванную взаимодействием между основными и вторичными гидравлическими трещинами.
Цель настоящей статьи заключается в изучении подходов к исследованию межскважинной интерференции в нефтегазовых коллекторах.
Межскважинная интерференция находится в центре внимания динамического анализа нефтегазовых коллекторов, который в основном изучается в двух аспектах – статическом и динамическом. Статический метод включает корреляцию межскважинных горизонтов, а динамический метод идентификации – анализ данных скважинных испытаний [3].
По сравнению с традиционными газовыми или нефтяными месторождениями, для добычи нефти из которых достаточным является гидравлический разрыв пласта, в коллекторах тяжелой нефти применяется многостадийный разрыв, в результате чего обычно образуются сложные сети трещин. Это предопределяет тот факт, что использование традиционных подходов, приемлемых для обычных коллекторов в процессе анализа межскважинной интерференции, сталкивается с рядом трудностей, когда речь идет о нефтегазовых коллекторах. Например, сложности возникают с анализом передачи давления в гетерогенных сетях трещин. Промысловые данные показывают, что для изучения межскважинной интерференции при многостадийном ГРП коллекторов с тяжелой нефтью больше подходит модель power-law, включающая неравномерную передачу давления в гетерогенных системах [4]. Таким образом, на основе модели силового закона создается метод диагностики в режиме реального времени для каждой стадии ГРП.
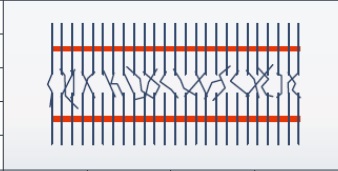
Рассмотрим особенности исследования межскважинной интерференции в нефтегазовых коллекторах на конкретном примере. Для этого используем физическую модель, которая представлена на рис. 2.
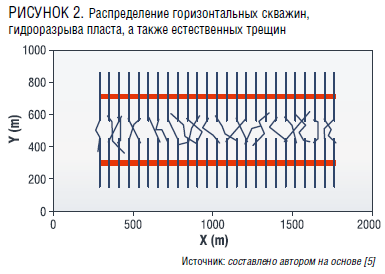
На рис. 2 показано, что две горизонтальные скважины соединены посредством гидравлических и естественных трещин. Интерференция скважин вызвана интерференцией трещин и интерференцией давления через гидравлические, естественные трещины и матрицы.
В сложных геологических условиях мгновенная передача давления в гетерогенных системах трещин не очень хорошо подчиняется закону Дарси, в то время как модель закона мощности может лучше описать характеристики изменения давления во времени и пространстве [5]. Выражение закона потока выглядит следующим образом:
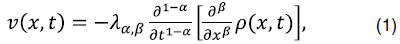
где x – расстояние, t – время, а P(x, t) – давление. Все 
, α и β меньше.
Пример расчета: при параметрах λα,β=0.05 м2/сλα,β = 0.05м2/с, α = 0.7α = 0.7, β = 0.8β = 0.8, ρ(x,t) = 1000 кг/м3 ρ(x,t)=1000кг/м3, x=50 мx=50м, t=10 чt=10ч: v(50,10)≈0.12 м/с.v(50,10)≈0.12м/с.
1. 
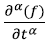– дробная производная по времени, 
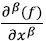– пространственная дробная производная, которые, соответственно, могут быть выражены следующим образом:
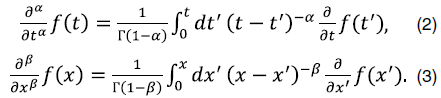
При постоянном темпе производства общее решение уравнения (1) получается из уравнений (2) и (3):
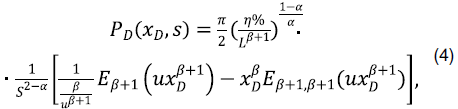
где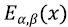 
– двухпараметрическая функция Миттага-Леффлера, а при = 0 решение уравнения (4) имеет следующий вид:
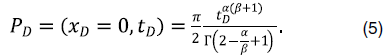
При индексе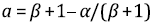 
можно получить 
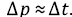При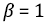 
решение 
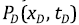находится таким образом:
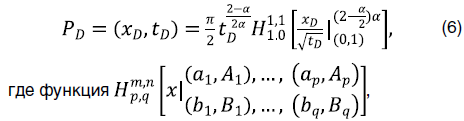
а показатель перепада давления в интерферирующих скважинах соответствует показателю в интерферирующих скважинах.
На основе выбранной физической модели нефтегазового коллектора для характеристики процесса просачивания с межскважинными интерференциями целесообразно использовать традиционную трехлинейную модель просачивания с замкнутыми внешними граничными условиями в зоне течения матрицы пласта. Затем с помощью преобразования Лапласа [6] может быть получено решение безразмерного псевдозабойного давления, соответствующего постоянному дебиту с учетом скин-эффекта.
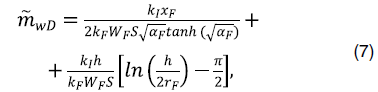
где mwD – безразмерное решение по псевдозабойному давлению, соответствующее постоянному расходу;
∼ представлено в пространстве Лапласа;
kI – проницаемость межразломной зоны течения;
xF – полудлина основной трещины; kF – проницаемость зоны потока основного разлома;
wF – ширина основного разлома;
s – параметр преобразования Лапласа;
rw – радиус ствола скважины;
αF – параметр гидравлического разлома в модели трилинейного потока.
Пример: для kI=0.1 мДkI=0.1мД, xF=100 мxF=100м, kF=10 мДkF=10мД, WF=0.01 мWF=0.01м, h=30 мh=30м, rw=0.1 мrw=0.1м, αF=0.5αF=0.5: m~wD≈15.7.mwD≈15.7
Параметр гидравлического разрыва определяется следующим образом:
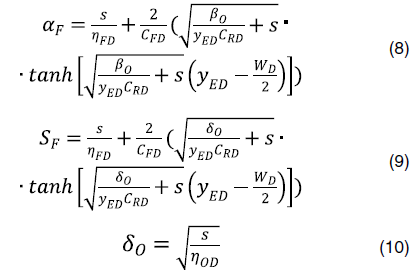
Матрица в основном играет роль накопителя, трещина является каналом просачивания, матрица дополняет флюид до трещины, учитывая изменение давления в матрице [7].
По мере того, как газ в матрице поступает в трещину и ствол скважины, адсорбированный газ в матрице десорбируется. Поскольку поровая вода в сланцевой матрице мала и в основном находится в виде водяной пленки, ей трудно участвовать в потоке, а канализирование водной фазы в твердой матрице не учитывается. Если взять в качестве примера газовое уравнение, то уравнение неразрывности имеет следующий вид:
Пример расчета:
Для примера рассмотрим параметры:
- Масса подвижного элемента: m = 5 кг;
- Начальная скорость: v = 10 м/с.
Тогда начальная кинетическая энергия по формуле (1) составит:
E_k = (1/2) * m * v^2 = (1/2) * 5 * 10^2 = 250 Дж.
Предположим, что после удара скорость уменьшилась до 4 м/с:
E_k' = (1/2) * 5 * 4^2 = 40 Дж.
Потери энергии составят:
ΔE = E_k - E_k' = 250 - 40 = 210 Дж.
Таким образом, эффективность ударного взаимодействия может быть оценена как:
η = E_k' / E_k = 40 / 250 = 0,16 (или 16%).
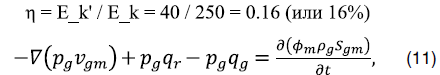
где 
представляет собой член десорбции в матрице, свободный объем воздуха при десорбции в порах матрицы на единицу объема, м3/(с×м3);
– плотность газовой фазы;
– пористость трещины;
qg – переток газа между трещиной и матрицей,
– объемный вес, который представляет собой произведение плотности и гравитационного ускорения;
– это двухфазное насыщение, безразмерное.
Согласно изотермической адсорбции Ленгмюра, с течением времени давление в матричной системе уменьшается и происходит десорбция газа [8,9]. Расчетное выражение выглядит следующим образом:
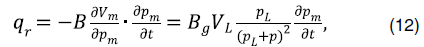
где B представляет собой объемный коэффициент;
Vm – количество газа, адсорбированного на единицу объема сланцевой матрицы;
, единица измерения м3/м3;
– давление в трещине;
– объем трещины;
– давление адсорбированного газа.
Пример расчета десорбции газа: B=1.2B=1.2, VL=0.5 м3/м3VL=0.5м3/м3, pL=10 МПаpL=10МПа, p=8 МПаp=8МПа, ∂pm/∂t=0.01 МПа/ч∂pm/∂t=0.01МПа/ч:
qr≈0.003 м3/(с⋅м3).qr≈0.003м3/(с⋅м3)
Геомеханические параметры (напряжение и деформация), рассчитанные по модели Бартона-Бандиса [10], связаны только с блоками матрицы, однако можно определить проницаемость трещин по нормальному эффективному напряжению трещины. Проницаемость закрытия трещины krcf (мД) описывается следующим уравнением:
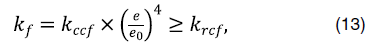
где kccf – проницаемость трещины при нулевом напряжении (мД);
– проницаемость трещины;
e – определяется как текущая апертура трещины;
e0 – начальная апертура трещины, т.е.
где 
представляет собой отношение жесткости напряжения к жесткости разрушения.
Используя полностью связанный трехмерный симулятор ГРП, геомеханики и пласта Multi-Frac-3D с композиционными, геомеханическими и термическими опциями, можно провести серию симуляций интерференции между скважинами с гидравлическим разрывом пласта. В базовом моделировании использовалась максимально простая постановка задачи, чтобы выделить основные свойства системы.
На рисунке 3 показана схема модели. Она состоит из двух скважин – добывающей и контрольной, соединенных прямоугольным разломом с постоянной проводимостью (рис. 3 б, 3 в).
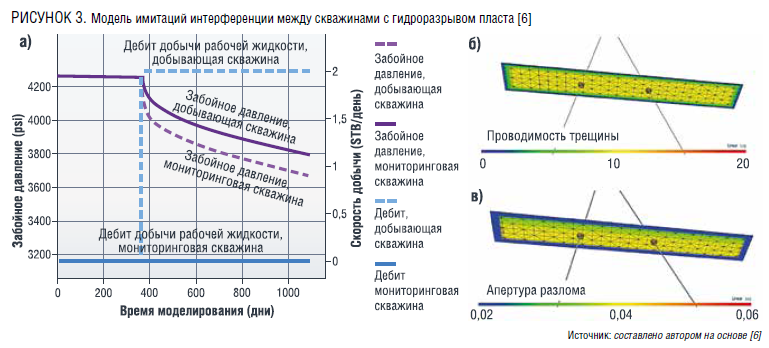
На рис. 3 a) установка для простых случаев с одним интерференционным тестом; 3 б) трещина с постоянной проводимостью, соединяющая две скважины; 3 в) почти однородная апертура трещины.
На граф. 4. показаны графики зависимости давления от расстояния на основании приведенным расчетам.
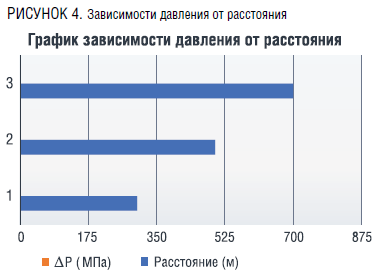
Для простоты расчетов процесс гидроразрыва и размещения проппанта не моделируется, а принимается в их стандартной формализации. В свою очередь, трещина задается как уже существующая с известными свойствами. Начальная апертура трещины формализуется в общих значениях. Апертура трещины рассчитывается как функция эффективного нормального напряжения с помощью уравнения Бартона-Бандиса. Параметры уравнения Бартона-Бандиса выбираются таким образом, чтобы сжимаемость трещины была практически постоянной в диапазоне условий моделирования и разумной для проводимости пачки проппанта (~ 0,01 МПа-1). В каждом моделировании проводимость трещины устанавливается на постоянное, равномерное значение.
В базовом моделировании используется однофазная слабосжимаемая жидкость. Проницаемость однородна, а поровое давление гидростатично. Вязкость воды составляет 0,31 сП, а сжимаемость флюида – 0,000435 МПа-1. В начале моделирования обе скважины заглушены. Добывающая скважина вводится в эксплуатацию с граничным условием постоянного дебита жидкости 2 барреля в сутки, как показано пунктирной синей линией на рис. 3 a). После запуска скважины в эксплуатацию забойное давление мониторинговой скважины начинает снижаться. Первоначальное базовое моделирование проводилось при проводимости трещин 0,1, 1, 10 и 100 миллидарси-футов.
Проникновение трещин при различных расстояниях между скважинами изучалось при условии одинакового масштаба гидроразрыва, результаты испытаний показаны на рис. 4. Тепловизионное изображение трещин с расстоянием между скважинами 370 м показывает очевидное проникновение трещин и большое перекрытие. Когда расстояние между скважинами составляет 617 м, тепловизионное изображение трещин демонстрирует, что область перекрытия трещин мала.
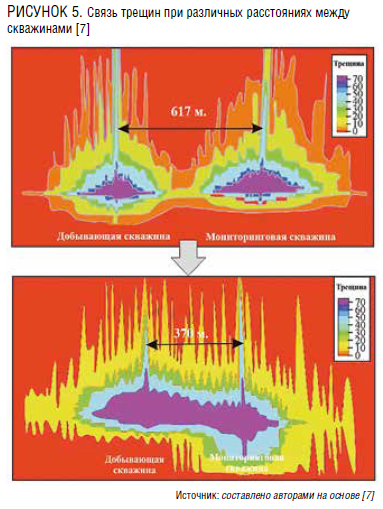
Таким образом, расстояние между скважинами в оптимизированной зоне составляет 370–617 м. Для горизонтальных скважин с расстоянием между ними менее 300 м, хотя масштаб гидроразрыва строго контролируется, межскважинная интерференция все равно будет иметь место. Для горизонтальных скважин с расстоянием между скважинами более 700 м существует вероятность того, что пласт не будет освоен из-за недостаточного масштаба ГРП. Таким образом, рекомендуемое расстояние между скважинами на моделируемом нефтегазовом месторождении составляет 500–700 м. Одновременно следует учитывать тот факт, что даже если в процессе гидроразрыва не происходит каналирования давления, в процессе добычи из-за продолжительной выработки давление будет распространяться вдоль матрицы, что приведет к увеличению интерференции между скважинами.
Для изучения степени интерференции между скважинами после заполнения существующей схемы скважин средняя площадь контроля скважины в блоке заполнения приводится к моделируемой скважине с помощью технологии численного моделирования.
Таким образом, подводя итоги проведенного исследования, можно сделать вывод о том, что межскважинная интерференция является серьезной проблемой, препятствующей оптимальному извлечению углеводородов из нефтегазовых месторождений. Изучение данных вопросов началось сравнительно недавно, поэтому важно понять основные причины и методы, которые приводят к ее возникновению, что позволит разработать оптимальные стратегии управления добычей, а непрерывный поверхностный и скважинный микросейсмический мониторинг предоставляет уникальную возможность оценить связь и помехи давления между скважинами.
Литература
1. Волошин Г.В. Эффекты интерференции различных каналов импульсного возбуждения резонансов когерентного пленения населенностей в ячейках с парами щелочного металла и буферным газом / Г.В. Волошин // Журнал экспериментальной и теоретической физики. – 2024. – Т. 165. – № 5. – С. 607–617.
2. Гималтдинов И.К. Детонация газожидкостной смеси при интерференции волн на наклонной границе / И.К. Гималтдинов, А.С. Родионов, Е.Ю. Кочанова // Физика горения и взрыва. – 2023. – Т. 59. – № 3. – С. 36–43.
3. Кааров Ж.З. Разработка методов оптимизации размещения горизонтальных скважин в газовых и газоконденсатных залежах / Ж.З. Кааров // Инновации. Наука. Образование. – 2022. – № 49. – С. 1326–1331.
4. Левитина Е.Е. Оценка динамики пластового давления и дренируемых запасов газа по данным исследований скважин эксплуатационного фонда / Е.Е. Левитина, Е.И. Инякина, Н.М. Паклинов // Известия высших учебных заведений. Нефть и газ. – 2023. – № 5 (161). – С. 67–76.
5. Zhuang, HuiNong et al. Dynamic Well Testing in Petroleum Exploration and Development. Second edition / Huinong Zhuang, Yongxin Han, Hedong Sun, Xiaohua Liu. Amsterdam: Elsevier, 2020. 198 p.
6. Almasoodi, M., Andrews, T., Johnston, C. A new method for interpreting well-to-well interference tests and quantifying the magnitude of production impact: theory and applications in a multi-basin case study / M. Almasoodi, T. Andrews, C. Johnston // Geomech. Geophys. Geo-energ. Geo-resour. – 2023. – № 9. – Р. 95–97.
7. Zhou, Y. Multiple Hydraulic Fractures Growth from a Highly Deviated Well / Y. Zhou, D. Yang. Mechanics of Hydraulic Fracturing. 2022. 129 p.
8. Qing Zhang Well Interference Analysis of Shale Gas Wells Based on Embedded Discrete Fracture Model // Geofluids. 2022. Volume 2022, Issue 1. Р. 105–113.
9. Wei Liang Opportunities and challenges for gas coproduction from coal measure gas reservoirs with coal-shale-tight sandstone layers: A review / Liang Wei, Wang Jianguo // Deep Underground Science and Engineering. – 2024. – Volume 4. – Issue 1. – Р. 20–29.
10. Weilin Ye Research on temperature and pressure interference in photoacoustic spectroscopy gas detection / Ye Weilin, Luo Wenxuan // Microwave and Optical Technology Letters. – 2023. – Volume 66. – Issue 1. – Р. 109–118.
