Природный газ в естественных условиях контактирует с краевой (подошвенной) и погребенной водой, поэтому он насыщен парами воды. При пластовых температурах, превосходящих 473,15 К, и средних давлениях содержание паров воды в газе становится очень большим, а при высоких давлениях значительно увеличивается растворимость газа в погребенной воде. Вследствие этого водяной пар, содержащийся в природном газе, может заметно изменять его объемные свойства, что необходимо учитывать при подсчете запасов и разработке глубокозалегающих газовых месторождений [1].
Для оценки запасов природного газа, залегающего в пластах в условиях высоких температур и давлений, а также выбора оптимального режима его добычи необходимо знание термодинамических свойств газа в зависимости не только от температуры и давления, но и от растворимости газа в воде и растворимости воды в газе (при высоких температурах).
В данной работе по экспериментальным данным о (p,rм,T)x=(p,Vм,T)x-зависимостях модели природного газа (система метан – вода) по изотермам (523,15–653,15 К) [1–3] получено трехпараметрическое полиномиальное уравнение состояния в виде разложения фактора сжимаемости Z в ряды по степеням приведенной плотности ω=ρ/ρк, приведенной температуры τ=T/Tк и состава х: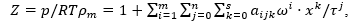 
, или 
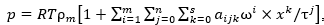описывающее экспериментальные значения давления газовой фазы системы метан – вода со средней относительной погрешностью 0,9 %.
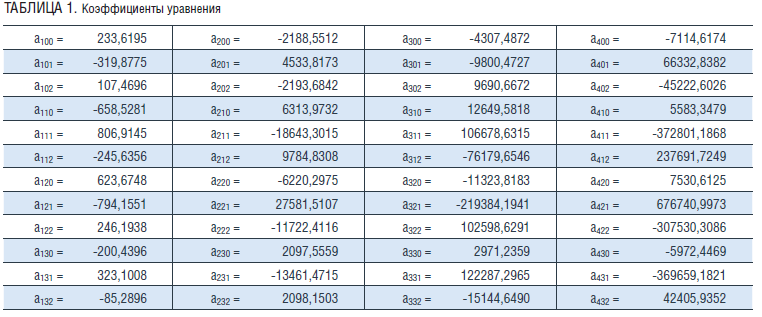
Коэффициенты уравнения (таблица 1) определены по экспериментальным р,ρ,Т,х – данным [1–3] усовершенствованным методом наименьших квадратов [4–6], предварительно согласовав функцию p(w,t)x и ее производные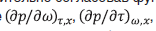 
, 
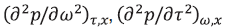на границах областей действия уравнения [5, 7, 8].
Расчет термодинамических свойств
Из-за большого объема материала ниже приведены результаты расчета для смеси состава 0,5 мольные доли, а зависимость термодинамических свойств от концентрации для плотности смеси 30 кг/м3. Характер изменений основных термодинамических свойств смеси всех исследованных составов идентичен.
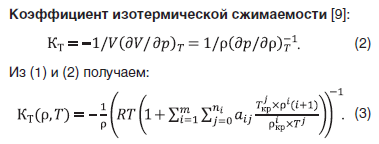
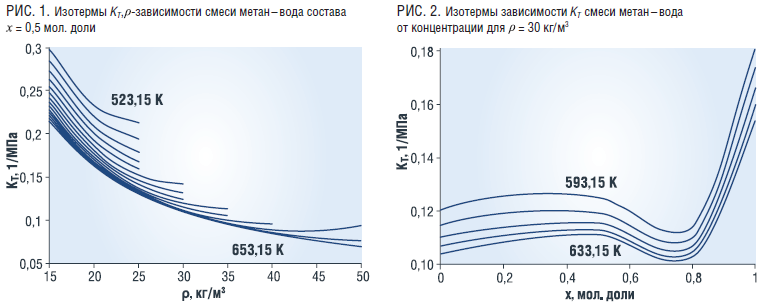
Как видно из рис. 1, величина КT смеси падает с ростом плотности. С ростом концентрации величина КT слабо растет до концентрации 0,6 мол. доли воды, проходит минимум при значении 0,8 мол. доли воды и далее резко растет (рис. 2).
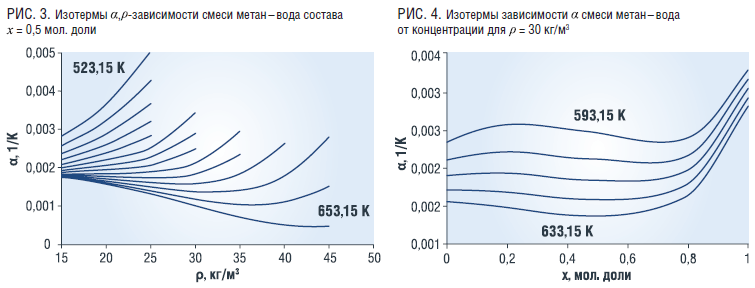
Характер зависимости α смеси от плотности и температуры аналогичен характеру зависимости КT (рис. 3). Величина α практически не зависит от концентрации в пределах до х=0,8 мол. доли воды, а при больших концентрациях растет (рис. 4).
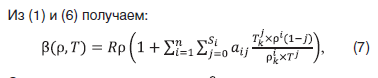
С ростом плотности величина β смеси растет для всех изотерм кроме Т=653,15 К (рис. 5). С ростом концентрации воды величина β практически не меняется (рис. 6).
Внутреннее давление
Общее давление p в реальной системе зависит от интенсивности теплового движения молекул pк (кинетическое давление) и межмолекулярного взаимодействия pв (внутреннее давление) [10, 11], т.е.
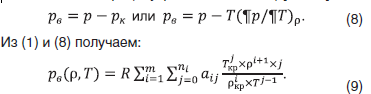
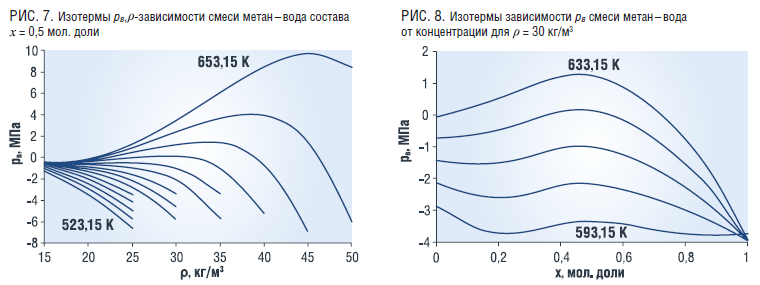
Величина pв смеси убывает с ростом плотности (рис. 7), но для температур Т>633,15 К сначала наблюдается рост и убывает с ростом плотности. С ростом концентрации воды характер поведения pв смеси аналогичен величине β (рис. 8).
Величину внутреннего давления смеси pв можно выразить через коэффициенты изотермической сжимаемости (2) и объемного термического расширения (4):
Основные термодинамические свойства смесей можно рассчитать, как изменение их относительно идеально-газового состояния при давлении 0,1 МПа в диапазоне исследованных температур.
Изохорная теплоемкость
Для расчета изохорной теплоемкости смесей [9]
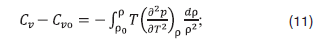
необходимо знать ее значения в идеально-газовом состоянии 
. Для этого запишем выражение для изобарной теплоемкость смесей в идеально-газовом состоянии [12]:
где и – изобарные теплоемкости в идеально-газовом состоянии воды и метана соответственно, определяемые эмпирическим уравнением [12]
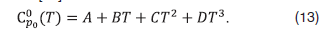
Значения коэффициентов уравнения (13) взяты из [12], приведены в таблице 3.
Следовательно, величина изохорной теплоемкости смесей в идеально-газовом состоянии равна:
Из уравнения (1) с учетом (11) и (14), получим выражение для расчета величины изохорной теплоемкости смесей:
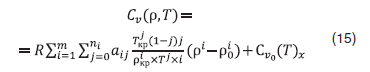
Как видно из рис.9, Cv при всех температурах плавно растет с ростом плотности, а в зависимости от концентрации воды (рис. 10) имеет минимум в диапазоне х=0,6–0,8 мол. доли воды.
Изобарная теплоемкость
Характер зависимости изобарной теплоемкости смесей от температуры, плотности и состава, рассчитанной по выражению [9]
иллюстрируют рис. 12 и 13.
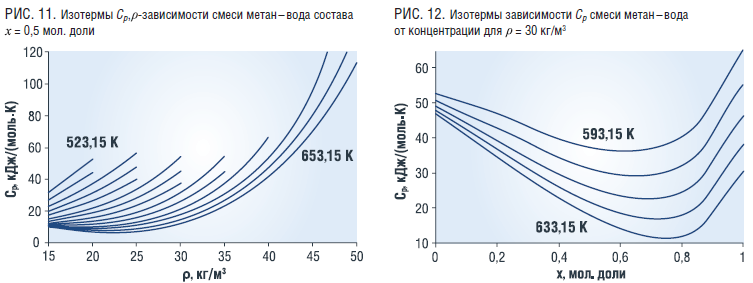
Изобарная теплоемкость смеси в зависимости от плотности имеет поведение аналогично изохорной (рис. 11), а концентрационная зависимость аналогична изохорной теплоемкости (рис. 12).
Скорость звука
Данные о скорости распространения звука в смеси вместе с данными о ее плотности могут быть использованы для построения термодинамических энтропийных диаграмм, необходимых для расчета тепловых процессов, происходящих в экстракционных и энергетических установках. Зависимость скорости распространения звука в среде от плотности и температуры определяется выражением [9]:
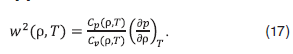
Величина скорости звука w в смеси уменьшается с ростом плотности (рис. 13). Концентрационная зависимость w имеет максимумы при х=0,8 мол. доли воды, которые увеличиваются с ростом температуры (рис. 14).
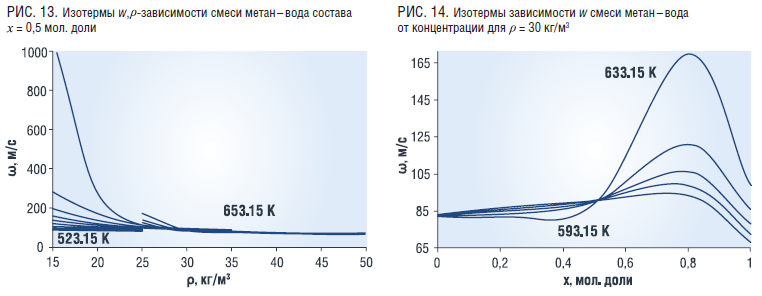
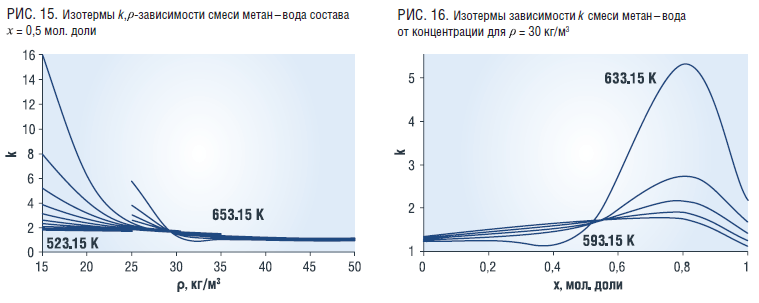
Показатель адиабаты k смеси имеет аналогичную зависимость от плотности и температуры и от концентрации, как и скорость звука w (рис. 15, 16).
Энергия Гельмгольца
Выражение для расчета изменений энергии Гельмгольца чистого вещества относительно идеально-газового состояния [12]
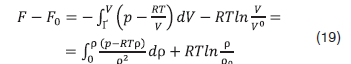
применимо и для смеси постоянного состава (x=const). Энергия Гельмгольца смеси в идеально-газовом состоянии равна
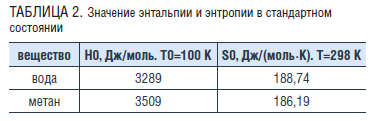
В таблице 2 приведены взятые из работ [13, 14] значения энтальпии H0 при температуре Т0=100 К и энтропии S0 при температуре Т0=298 К для чистых веществ в идеально-газовом состоянии.
Из уравнения (1) с учетом (19)–(22) получаем выражение для расчета энергии Гельмгольца смеси постоянного состава (x=const) в зависимости от плотности и температуры:
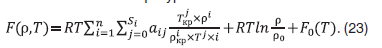
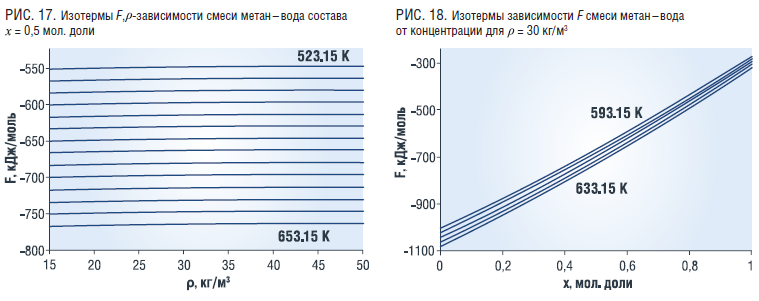
Энергия Гельмгольца смеси метан–вода состава x=0,5 мол. доли уменьшается с ростом температуры и незначительно растет с ростом плотности (рис. 18). С ростом концентрации воды величина энергии Гельмгольца увеличивается независимо от температуры (рис. 19).
Энтропия
Изменение энтропии смеси постоянного состава относительно идеально-газового состояния можно рассчитать по выражению [12]
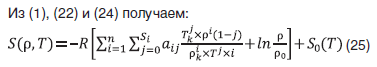
Энтропия смеси метан–вода состава x=0,5 мол. доли убывает с ростом плотности и возрастает с ростом температуры (рис. 19). Величина энтропии с ростом концентрации воды падает (рис. 20).
Энтальпия
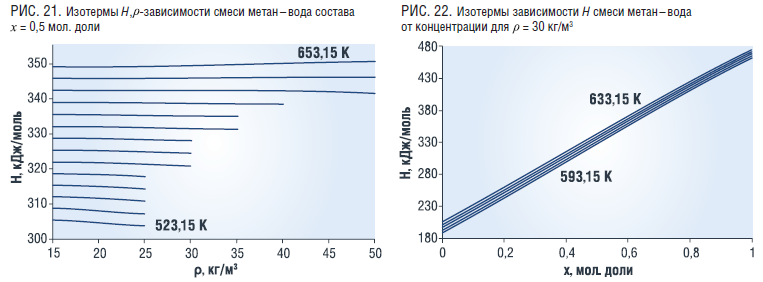
На рис. 22 представлена зависимость энтальпии смеси вода–этанол состава x=0,5 мол. доли от плотности и температуры, рассчитанная по выражению [12]
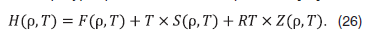
Как видно, величина энтальпии смеси с ростом плотности слабо убывает, а для температур выше 643,15 К немного растет (рис. 21). Характер концентрационной зависимости энтальпии иллюстрирует рис. 22.
Внутренняя энергия
Выражение для внутренней энергии смеси постоянного состава имеет вид:
Подставляя в (27) значения энергии Гельмгольца (23) и энтропии (25), рассчитаны значения внутренней энергии смесей. Зависимость величины U от плотности, температуры и состава смеси представлена на рис. 23 и 24.
Характер поведения внутренней энергии аналогичен поведению энтальпии (рис. 21 и 22).
Энергия Гиббса
Зная зависимость энтальпии и энтропии смеси постоянного состава от плотности и температуры, можно рассчитать энергию Гиббса.
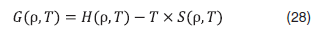
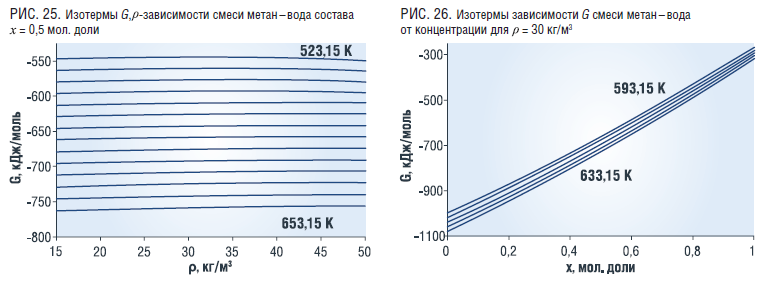
Зависимость энергии Гиббса от плотности, температуры и концентрации (рис. 25 и 26), аналогична зависимости энергия Гельмгольца (рис. 17 и 18).
Дифференциальный изотермический дроссельный эффект представляет собой уменьшение энтальпии смеси при медленном протекании ее под действием постоянного перепада давлений сквозь пористую перегородку без изменения температуры:
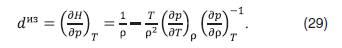
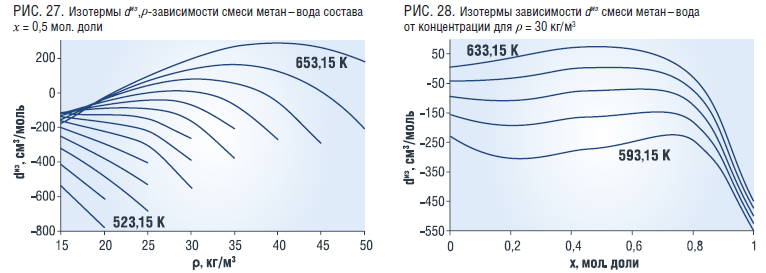
Величина изотермического дроссельного эффекта с ростом плотности смеси вначале убывает (для Т<613,15 К), и для Т>613,15 К плавно растет, имеет максимумы в зависимости от температуры и с ростом плотности убывает (рис. 27). Величина dиз от концентрации х=0,8 мол. доли практически не зависит, а далее уменьшается с ростом концентрации (рис. 28).
Дифференциальный адиабатный дроссельный эффект – это изменение температуры смеси при медленном протекании ее под действием постоянного перепада давлений сквозь пористую перегородку без теплообмена с внешней средой:
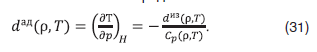
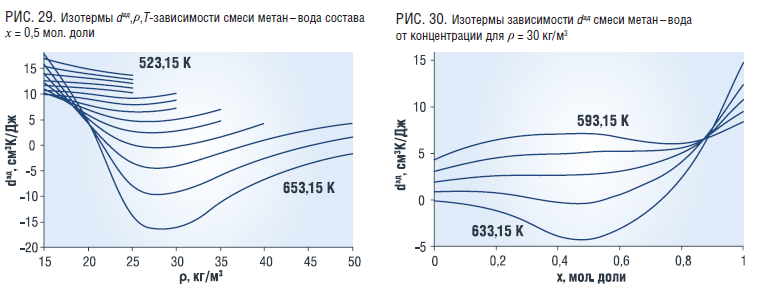
Адиабатический дроссельный эффект с ростом плотности и температуры убывает, имеет минимум при ρ~30 кг/м3 и далее плавно растет (рис. 29). Концентрационная зависимость dад имеет особенность в области х~0,9 мол. доли воды (рис. 30).
