Ключевые слова: прогноз нефтегазоносности, термическая конвекция, угол и скорость субдукции, реологические параметры, фазовые переходы, аномалии теплового потока.
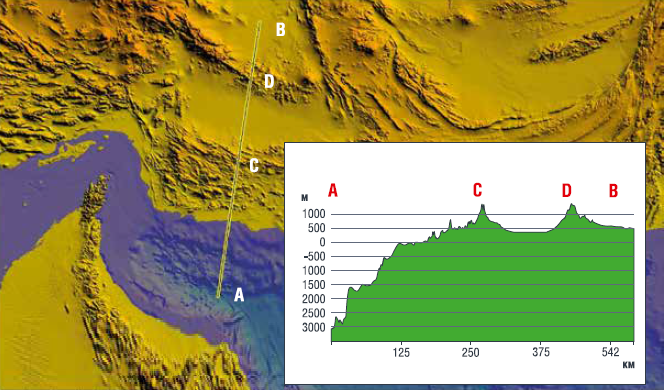
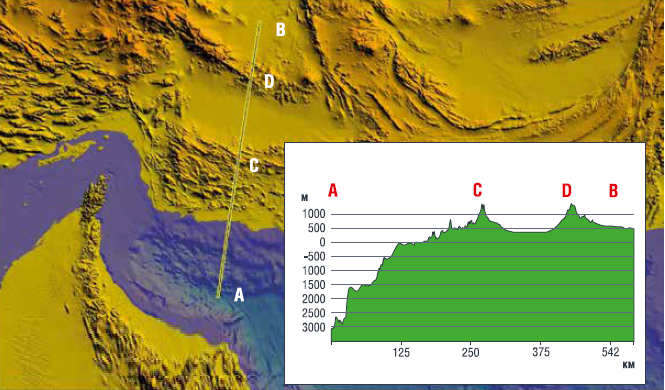
Для устойчивого экономического развития и в связи с возросшими потребностями на потребление электроэнергии некоторые страны Азии (Пакистан, Ирак, Иран) хотят найти на своей территории новые месторождения нефти и газа. В связи с этим различные российские специалисты и некоторые геолого-разведочные компании стараются помочь этим странам Азии в поисках месторождений углеводородов. Многие из стран Азии расположены в зонах, где часто происходят землетрясения. При этом создаваемые землетрясениями пластовые давления, как известно, влияют на дебит добычи нефти. Рассмотрим такую нефте- и газоперспективную зону Макран, расположенную на побережье Персидского залива. Общий вид обзорной карты с изображением рельефа поверхности в районе исследований показан на рис. 1.
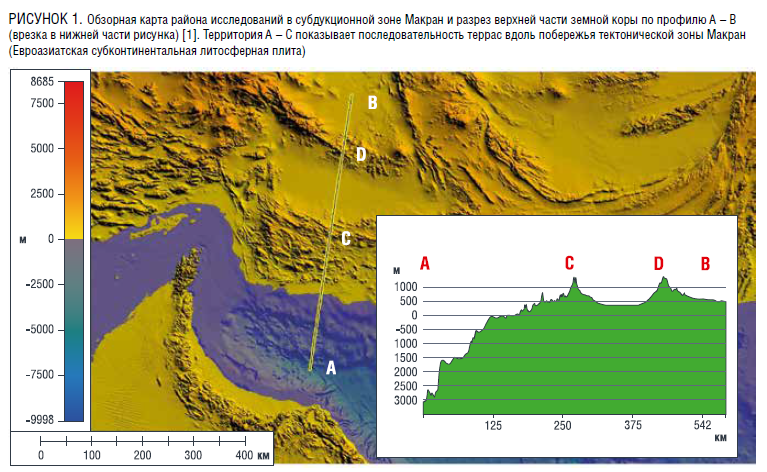
Зона субдукции Макран практически широтного простирания расположена у южного побережья Ирана и Пакистана и уникальна в том, что скорости субдукции океанической части Аравийской литосферной плиты различны по обеим сторонам левостороннего разлома Зонне со смещением по простиранию, расположенного вдоль меридиана на 59,5ºЕ, и разделяющего зону субдукции Макран на две части. На Иранской (западной) части поддвигание происходит со скоростью 20,4 мм∙год–1, а на Пакистанской (восточной – со скоростью 32,6 мм·год–1, причем на Иранской части желоба субдукция идет в режиме асейсмичного скольжения, а на Пакистанской части – в ходе последовательности сильных землетрясений, последнее из которых (с магнитудой Mw = 8,1) произошло 27 ноября 1945 года. Предыдущие сильные землетрясения случились на Пакистанской части желоба Макран в 1851 году (западнее зоны землетрясения 1945 года) и в 1765 году (восточнее этой зоны), так что в настоящее время на Пакистанской части желоба Макран, по-видимому, подготовлено очередное сильное землетрясение. Согласно [1], распределение фокусов землетрясений по глубине севернее 27º N свидетельствует, что средний угол субдукции составляет ~ 26º, а из рис. 3 этой статьи видно, что севернее приблизительно 29º N угол субдукции ~ 24º. Прежние данные об отраженных сейсмических сигналах интерпретировались как свидетельства в пользу крайне пологой субдукции, происходящей под углом ~ 2–3º до глубин в несколько десятков километров [1], однако этот вывод можно отнести только к неглубокой части субдуцирующего блока.
В работе [2] на рис. 5 и в тексте представлены сведения о расположенной при ~ 33º N параллельной зоне субдукции Макран 2D-зоне аномального повышенного теплового потока с дневной поверхности (рис. 2).
РИСУНОК 2. Карта двух основных линейных зон (C и D) аномалий теплового потока, связанных с поддвигом океанической части Аравийской литосферной плиты под Евроазиатскую субконтинентальную литосферную плиту
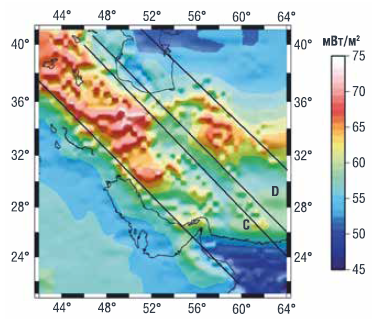
Максимум теплового потока ~ 67 мВт∙м –2 расположен в тылу западной (Иранской) части желоба Макран, а позади восточной (Пакистанкой) части желоба аномалия теплового потока менее ~ 63 мВт∙м –2. Поперечный размер зоны аномального теплового потока составляет ~200 км, и происхождение этой зоны, по-видимому, связано с 2D конвективным потоком в мантийном клине, восходящим к подошве настилающей Евроазиатской литосферы и локализующим вынос диссипативного тепла. В работе [3] показывается, что 2D-конвекция в мантийном клине, рассчитанная с учетом диссипативного тепловыделения, неньютоновской реологии мантии и влияния фазовых переходов на глубинах 410 и 660 км, действительно обеспечивает вынос разогретого мантийного материала конвективным потоком шириной ~ 200 км на расстоянии ~ 500 км к северу от желоба Макран, где и наблюдается зона аномального теплового потока. Конвективный поток из мантии может выносить к поверхности Земли мантийные углеводороды и щелочные металлосодержащие внедрения (железосодержащие руды). В работе [2] отмечается, что поверхностный тепловой поток является важным указателем наличия в недрах Земли углеводородных резервуаров и перспективных источников минеральных ресурсов. Меньший тепловой поток, вероятно, объясняется прерывистым режимом субдукции в восточной (Пакистанской) части желоба Макран и, как следствие, более высоким содержанием кристаллизационной воды в мантийном клине. Согласно [4], содержание воды в мантийном клине, выжимаемой из погружающегося литосферного блока, достаточно велико и может достигать нескольких весовых процентов. Вследствие этого в мантийных клиньях доминирует дислокационная неньютоновская ползучесть, при которой коэффициент эффективной вязкости обратно пропорционален степенной функции концентрации воды Cw и уменьшается с увеличением Cw. В [4] на с. 167 указывается, что наличие воды в мантийном клине провоцирует сейсмичность через механизм неустойчивости, но имеется и обратная связь сейсмичности и содержания воды через механизм «встряхивания» субдуцирующего блока и более активного выжимания воды. В силу этого вязкость в мантийном клине над литосферным блоком, субдуцирующим в прерывистом режиме в ходе последовательности землетрясений понижается, кроме того, с ростом содержания воды (т.е. увеличением влажности материала мантийного клина) снижается энергия активации, что еще более уменьшает вязкость и, следовательно, уменьшается диссипативное тепловыделение в мантии. Совместное действие этих причин понижает аномальный тепловой поток с дневной поверхности. Описанный механизм понижения теплового потока в тылу зоны субдукции, в которой происходят землетрясения, альтернативен описанному в [5], где на основе моделирования напряженного состояния в зоне трения субдуцирующего блока с настилающей литосферой показывается, что фрикционное тепловыделение в зоне трения меньше в случае прерывистого режима субдукции и в силу этого тепловой поток диссипативного происхождения уменьшается.
Геотермическое моделирование процессов в зоне субдукции
Опишем вначале построение термомеханической модели мантийного клина в Иранской части зоны субдукции Макран, в которой имеет место асейсмичное скольжение. Предполагая, что в западной (Иранской) части зоны Макран происходит асейсмичная субдукция, примем модель мантийного клина в этой зоне, рассчитываемую при условии равномерного поддвигания Аравийской плиты, т.е. будем считать, что субдукция происходит не в процессе прерывистого движения в ходе последовательности сильных землетрясений, а квазиравномерно. Такое предположение, основывающееся на данных работы [1], может быть существенным для обоснования используемых в модели граничных условий прилипания вязкого вещества мантийного клина, как к подошве настилающей литосферы, так и к поверхности субдуцирующей Аравийской плиты. При прерывистом (скачкообразном) режиме субдукции материал неньютоновской вязкой жидкости, моделирующей мантийный клин, может проскальзывать вдоль границ с литосферными плитами из-за повышения скоростей деформации в мантийном клине вблизи этих границ, и граничное условие прилипания может нарушаться. В качестве модели термомеханического состояния мантийного клина между подошвой Евроазиатской литосферной плиты, на которой находится тыловая зона западной (Иранской) части зоны субдукции Макран и поверхностью океанической части Аравийской литосферной плиты, поддвигающейся под побережье Ирака и Ирана под углом β со скоростью V, примем модель, получаемую при бесконечном числе Прандтля (Pr→∞) в приближении Буссинеска из системы двумерных безразмерных уравнений гидродинамики для функции тока ψ и температуры T [6]:
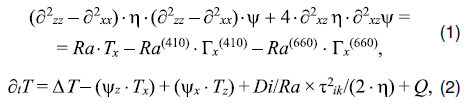
здесь h – безразмерный коэффициент динамической вязкости, символ ∂ и индексы означают частные производные по координатам x (горизонтальной), z (вертикальной) и времени t, D – оператор Лапласа, Гx(410) и Гx(660) – объемные доли тяжелой фазы на фазовых переходах на глубинах 410 и 660 км, компоненты скорости Vx и Vz связаны с функцией тока как:
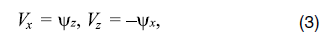
а безразмерные числа Рэлея Ra, фазовые Ra(410), Ra(660) и диссипативное Di есть:
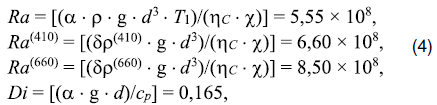
где a = 3 × 10-5 K-1 – коэффициент теплового расширения, r = 3,3 × 103
(кг × м-3) – плотность мантии, g – ускорение силы тяжести, cp = 1,2 × 103
Дж × кг-1 × K-1 – удельная теплоемкость при постоянном давлении, T1 = 1950°К – температура у основания переходной зоны мантии (ПЗМ) на глубине 700 км, считающейся нижней границей модельной области, Q = 6,25 × 10-4
мВт × м-3 – объемная мощность тепловыделения в оре, tik
– тензор вязких напряжений, d = 700 км – вертикальный размер модельной области, hC
= 1018 Па × с – масштабный множитель вязкости, c = 1 мм2 × с-1 – коэффициент температуропроводности, dr(410)
= 0,07r и dr(660) = 0,09r – скачки плотности на фазовых переходах на глубинах 410 и 660 км. В уравнениях (1), (2) масштабными множителями для времени t, напряжений tik
и функции тока y служат соответственно величины (d2
× c-1), (d–2 × hC × c) и c. Ранее в [7] строилась модель термомеханического состояния мантийного клина под Западно-Сибирской плитой в предположении линейной реологии для диффузионного механизма ползучести, доминирующего в мантии на глубинах более ~ 200 км [8], зависимость коэффициента вязкости от температуры T и литостатического давления p принималась в виде [4]:
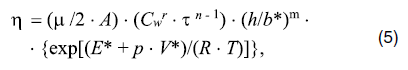
где для «влажного» оливина A = 5,3.1015
с-1, m = 2,5, размер зерна h = 10-1 – 101
мм, вектор Бюргерса b* = 5.10-7 мм
[9], энергия активации E* = 240 кДж.моль-1, объем активации V * = 5´103
мм3.моль-1, = 300 ГПа – нормирующее значение модуля сдвига, R – универсальная газовая постоянная. При этих значениях констант, выбранном масштабном множителе
= 1018 Па . с и размере зерна h = 1,6 мм безразмерный коэффициент вязкости, который также обозначается через
, равен:
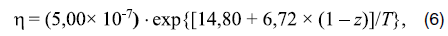
где T – безразмерная температура, а безразмерная координата z, нормированная на d, отсчитывается вверх от основания ПЗМ (ось x направлена по нижней границе ПЗМ против субдукции). Чтобы проверить, насколько для получаемых оценок скорости субдукции океанической части Аравийской литосферной плиты существенно предположение о линейной реологии мантии, в настоящей работе проведен расчет для неньютоновской реологии, для которой формулы вязкости (5), (6) переписываются в виде:
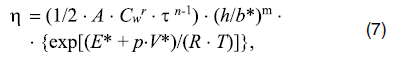
где, согласно [10], для горных пород с преобладающим содержанием оливина с повышенным содержанием в нем весовой доли воды (%), условно называемых породами «влажного» оливина, соответствуют следующие физические параметры: n = 3, r = 1,2, m = 0, t = (tik2)1/2, E* = 480 кДж × моль-1, V* = 11 × 103 мм3 × моль-1, A = 102 с-1 × (МПа)-n, Cw 10-3. Следует отметить, что значения констант в (7) у разных авторов, на которых приводятся ссылки в [10], весьма разнятся, и выше приведены усредненные значения. При
= 10-3 с учетом
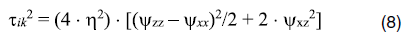
безразмерная вязкость есть
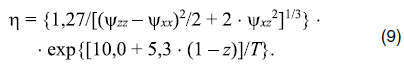
Отношение сторон модельной области примем равным 1 : 2,25, так что при субдукции по диагонали модельной области угол субдукции составит b ≈ 24o, а расчетная скорость V = 10 мм/год в единицах χ×d-1 равна V = 0,416 . 103, т.е. в субдуцирующей Аравийской литосферной плите ее компоненты Vx = –0,380 . 103 и Vz = –0,170 . 103.
Следуя [11], примем фазовые функции Г(l) в виде (напомним, что ось z здесь направлена вверх, поэтому знаки изменены):
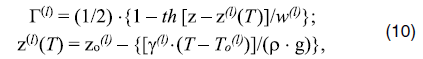
где z(l)(T) – глубина l-го фазового перехода, z0(l) и T0(l) – усредненные глубина и температура фазового перехода, g(410) = 3 Мпа × K-1 и g(660) = – 3 Мпа × K-1 – наклоны кривых фазового равновесия, w(l) – характерная ширина l-го фазового перехода, T0(410) = 1800°K и T0(660) = 1950°K – средние температуры фазовых переходов. Теплоты фазовых переходов, как и в [11], в формуле (2) не учитываются ввиду несущественности в случае развитой конвекции. Из формулы (10) получаем:
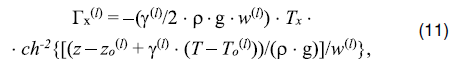
откуда видно, что фазовый переход с g(l) > 0 (при l = 410) усиливает конвекцию, а фазовый переход с g(l) < 0 (при l = 660) – ослабляет. В безразмерном виде z0(410) = 0,38, z0(660) = 0,99, w(l) = 0,05, g(410) = 2,55 × 109, g(660) = – 2,55 × 109, T0(410) = 0,92, T0(660) = 1, и тогда на этом основании формулу (11) можно переписать как:
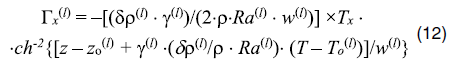
В качестве граничных условий приняты изотермичность горизонтальных и вертикальных границ, условия прилипания и непроницаемости границ (кроме «окон» внедрения и выхода субдуцирующей плиты, в которых задана скорость субдукции, и проницаемости удаленной от зоны субдукции границы под прямым углом, близким к углу выхода вынужденного мантийного потока при пологой субдукции). Величина Q в формуле (2) отлична от нуля в континентальной и океанической коре мощностью 40 км и 7 км соответственно. Начальная температура вертикальных границ принята по модели охлаждения полупространства в течение 1 млрд лет для Евроазиатской литосферной плиты и 100 млн лет для Аравийской плиты.
Сравнительные характеристики мантийного клина в Пакистанской и Иранской частях зоны субдукции Макран
Для первоначальной оценки того, насколько характеристики термомеханического состояния мантийного клина в Пакистанской части желоба Макран отличаются от характеристик, относящихся к Иранской части желоба, примем параметры среды равными их средним значениям, т.е. усредненным по горизонтальному и вертикальному размерам области максимального диссипативного тепловыделения. В этом случает можно считать, что коэффициент вязкости η, температура T, вязкое напряжение τ = ηV·d–1 (V – скорость субдукции, d – вертикальный размер рассматриваемой области мантийного клина) являются константами. При этом зависимость коэффициента вязкости от температуры, концентрации воды и других параметров среды учитывается усреднено, т.е. множители, входящие в реологический закон вязкости, считаются равными их средним значениям. По сравнению с Иранской частью мантийного клина, в Пакистанской его части концентрация воды повышается вследствие связи сейсмичности с наличием воды, а величины T, τ2·η–1 должны быть уменьшены на ~ 8 %, т.е. настолько, насколько тепловой поток, наблюдаемый в тылу Пакистанской части желоба, меньше наблюдаемого в тылу Иранской части желоба. Как видно из дальнейшей оценки, увеличение концентрации воды Cw влияет на тепловой поток преимущественно через уменьшение энергии активации среды, а не напрямую, поэтому в качестве первоначальной оценки содержания воды в Пакистанской части мантийного клина примем величину Cw = 2 весовых %, т.е. на 1 % больше, чем в Иранской части. C учетом формулы (7) для дислокационной вязкости в Пакистанской части зоны субдукции рассмотрим величину
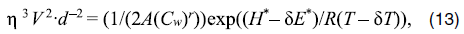
где H* – энтальпия активации, а δE* и δT – положительные величины возмущений энергии активации и средней температуры по сравнению с Иранской частью зоны субдукции.
Так как η·V2·d–2 (диссипативное тепловыделение) должно быть уменьшено на 8 %, то с учетом того, что V2·d–2 в Пакистанской части желоба выше в 2,25 раза, чем в Иранской (скорость субдукции в Пакистанской части выше в 1,5 раза), средний коэффициент вязкости оказывается меньше в 2,43 раза, а левая часть формулы (13) в 6,4 раза меньше в Пакистанской части зоны субдукции. Поэтому величина exp((H*– δE*)/R(T – δT)) в Пакистанской части зоны субдукции меньше, чем в Иранской части exp(H*/RT ) в 14,67 раза. Принимая δT = 0.08T, т.е что средний «температурный фон» на 8 % меньше в Пакистанской части зоны субдукции, находим, что при T = 1700 К оказывается δE* = 38 кДж·моль– 1. Аналогичная оценка, сделанная для содержания воды Cw = 1,5 весовых %, т.е. при повышении Cw в Пакистанской части мантийного клина на 0,5 весовых % по сравнению с Иранской дает δE* = 43,6 кДж·моль– 1.
Этот пример показывает, что понижение диссипативного теплового потока из мантийного клина может определяться не самим увеличением содержания воды, а связанным с ним понижением энергии активации. Хотя точных формул, описывающих уменьшение энергии активации при увеличении Cw не существует (о чем указывается в [4] на с. 274, где указывается, что энергия активации E* принимает лишь два значения: одно – для сухих пород и другое, меньшее, – для влажных), представляется вполне разумным найденное уменьшение энергии активации на ~ 8–9 % при увеличении концентрации воды на 0,5–1 весовых %, уменьшении теплового потока на 8 % и увеличении скорости субдукции в 1,5 раза в Пакистанской части зоны субдукции по сравнению с Иранской.
Принимая для Пакистанской части зоны Макран скорость субдукции равной 32,6 мм·год–1 (безразмерные компоненты скорости Аравийской плиты = – 0,620.103
и
= –0,280.103), угол субдукции приблизительно таким же, как в Иранской части зоны субдукции, энергию активации в формуле (7) E* = 440 кДж.моль-1 и Cw = 2 весовых %, находим, что мощность диссипативного тепловыделения и соответствующий тепловой поток в Пакистанской части желоба на ~ 5 % меньше, чем в Иранской части, а локализация конвективного теплового потока, выносящего диссипативное тепло из мантийного клина к дневной поверхности остается неизменной, т.е. такой же, как на рис. 2. Найденная модельная величина уменьшения мощности диссипативного тепловыделения и связанного с ним снижения аномального теплового потока с дневной поверхности удовлетворительно соответствует данным наблюдений в [2].
Результаты и обсуждение
Предполагая, что максимум теплового потока q возникает над конвективным течением, восходящим к зоне аномального теплового потока на Иранском плато на широте ~ 33ºN [2], и размер конвективной ячейки равен характерной ширине зоны повышенного теплового потока, можно оценить размер конвективной ячейки ~ 200 км. Для построения согласованной модели мелкомасштабной термической конвекции в мантийном клине между настилающей Евроазиатской литосферной плитой и субдуцирующей Аравийской плитой, ради повышения точности вычислений вначале необходимо положить в уравнениях (1)–(2) Ra→0, Di = 0, т.е. рассчитать модель погружающейся плиты, мантийного клина и настилающей плиты без учета вязкой диссипации и конвекции. Это связано с тем, что при значениях Ra и Di в формуле (4) конвекция в модели проходит стадии с большими скоростями, и для обеспечения устойчивости расчета квазистационарного состояния требуются крайне малые шаги по времени. При этом трудно рассчитать термическое состояние погружающейся плиты, настилающей плиты и индуцированного возвратного потока. Полагая вначале в уравнениях (1) – (2) Ra→0, Di = 0, т.е. учитывая только теплопроводность и адвекцию тепла (а также эффекты фазовых переходов), и интегрируя значения в уравнениях (1) – (2) по пространственным координатам методом конечных элементов на сетке 104´104 и по временнóй координате методом Рунге-Кутта 3-го порядка при V = 20 мм в год, получим квазистационарные безразмерные T = TR и ψ, изображенные на рис. 3, где изотермы показаны с интервалом 0,05, а линии тока – с интервалом 5.
РИСУНОК 3. (1) – квазистационарное распределение безразмерной температуры без учета эффектов вязкой диссипации и конвекции. Изотермы показаны с интервалом 0,05. (2) – квазистационарное распределение безразмерной невозмущенной функции тока в мантии над субдуцирующей Аравийской литосферной плитой без учета эффектов вязкой диссипации и конвекции. Линии тока показаны с интервалом 5. Диагональные эквидистантные линии тока соответствуют жесткой субдуцирующей плите, а вынужденные течения «А» и «В» индуцируются субдуцирующей литосферной плитой и отчасти конвективным механизмом. Расстояние отсчитывается от расположенного при 29 °N «краевого угла» мантийного клина в меридиональном направлении
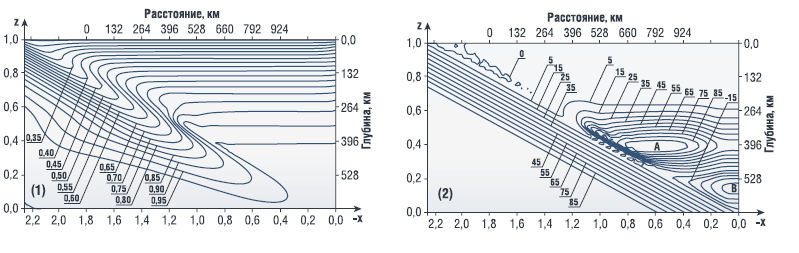
На рис. 3 показаны результаты расчета для неньютоновской реологии (формулы (7) – (9) для вязкости), причем на рис. 3 (1) показано распределение безразмерной температуры (изотермы), на рис. 3 (2) – безразмерная функция тока (линии тока).
Скорость V = 20 мм в год выбрана как подходящая современным геодезическим данным наиболее соответствующая наблюдаемому пространственному распределению теплового потока. Плита, субдуцирующая с заданной скоростью V, показанная равноотстоящими диагональными линиями тока, считается жесткой, а коэффициент вязкости в зоне трения литосферных плит при температурах ниже 1200°K понижается по сравнению с (7) на два порядка величины. Последним учтен эффект смазки за счет субдуцирующих осадков, которые частично затягиваются погружающейся плитой и препятствуют прилипанию к ней настилающей литосферы [12]. Из рис. 3 (2) видно, что возвратный поток, индуцируется в виде двух расположенных один над другим конвективных вихрей «А» и «В», верхний из которых (вихрь «А» с ψ > 0) вращается по часовой стрелке, а нижний («В» с ψ < 0) – против часовой стрелки. Конвективный вихрь «А» вызывается в мантийном клине отчасти вынужденным субдукцией вихрем «В», а отчасти конвективным механизмом, который нельзя полностью исключить, так как в уравнениях (1) – (2) число Рэлея не может быть положено в точности равным нулю (так как число Рэлея стоит в (2) в знаменателе). Из рис. 3 (2) видно, что в зоне «трения» индуцированного течения «А» и субдуцирующей плиты, движущихся навстречу друг другу, велик градиент скорости (т.е. скорость деформации), благодаря чему коэффициент вязкости (7) уменьшается на несколько порядков величины, и возможна инициация восходящего потока вихря Карига. В зоне трения микровихри течения «А» о субдуцирующую литосферную плиту объясняются неустойчивостью типа тангенциального разрыва, причем видно, что конвективный вихрь «А» отрывает от субдуцирующей литосферной плиты поверхностный слой мощностью ~ 30 км. Невозмущенная термомеханическая модель на рис. 3 возникает за безразмерное время t = 0,205283×10–2. Полагая затем безразмерные параметры в уравнениях (1)–(2) согласно формуле (4) , т.е. включая эффекты диссипации и конвекции, и интегрируя значения в уравнениях (1)–(2), находим, что в случае неньютоновской реологии при Cw = 1 весовых % вынужденный мантийный поток над субдуцирующей плитой за безразмерное время ~ 0,1´10–7 (в размерном виде ~ 103 лет) разрушается конвекцией, которая по достижении стадии развитой конвекции принимает вид, изображенный на рис. 4.
РИСУНОК 4. (1) – сглаженное распределение теплового потока q по [2] как функция расстояния x, отсчитываемого вдоль меридиана 58 °Е, перпендикулярного Иранскому сегменту зоны субдукции Макран. (График функции q(x) построен авторами данной работы); (2) – квазистационарное распределение безразмерной функции тока в мантии над субдуцирующей Аравийской литосферной плитой с учетом эффектов вязкой диссипации и конвекции в случаях неньютоновской реологии среды. Линии тока в литосферной плите показаны с интервалом 10, а в конвективных вихрях с интервалом 4 104. Вектор q указывает направление восходящего теплового потока, выносимого конвекцией. Нулевая линия тока соответствует состоянию покоя в Евроазиатской литосферной плите и/или разделяет противоположно вращающиеся конвективные вихри в мантийном клине
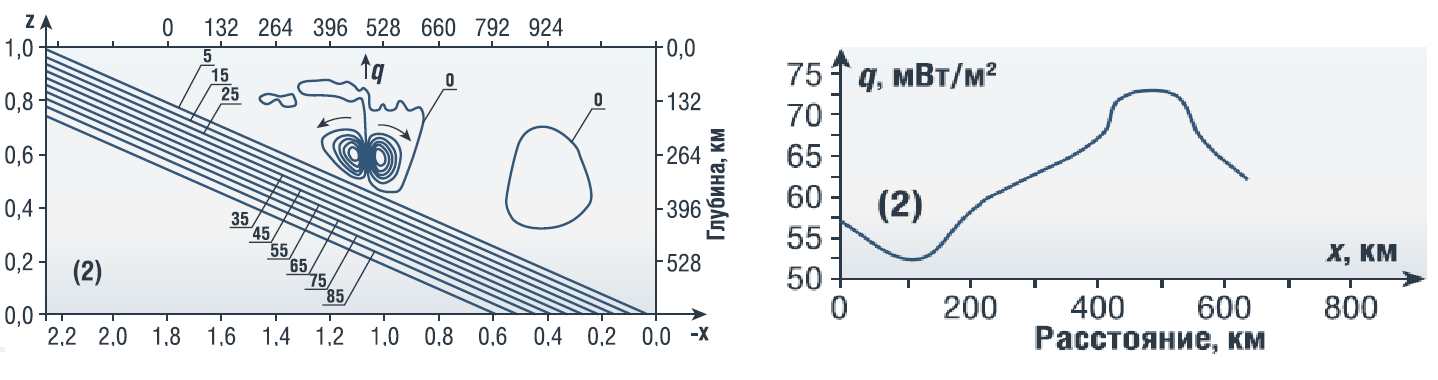
Видно, что вихревые линии тока, показанные с интервалом 4´104, действительно соответствуют одной конвективной ячейке, возбуждающейся при скорости субдукции V = 20 мм/год. Размер конвективной ячейки порядка 200 км, т.е. близок к наблюдаемой поперечной протяженности аномалии теплового потока на Иранском плато на широте ~ 33ºN (рис. 4). Расположение конвективной ячейки на расстоянии около 500 км от «острия» мантийного клина приблизительно соответствует 4º по долготе между широтой 29ºN, при которой угол субдукции резко возрастает до 24º, и широтой ~ 33ºN, на которой расположена зона повышенного теплового потока. Густота линий тока соответствует скорости конвективных движений более ~ 1 м×год-1. Таким образом, расчет для неньютоновской реологии с вязкостью в уравнениях (7) – (9) показывает, что при снижении вязкости на три порядка по сравнению с (7) – (9), т.е. при Cw = 1 весовых % в мантийном клине развивается конвекция в виде двух микровихрей, могущая обеспечить аномальный 2D тепловой поток. Значительная скорость конвективных движений объясняется локальным снижением вязкости за счет повышения напряжений в мантии в зоне, охваченной конвекцией. Отметим, что в случае ньютоновской реологии образование в мантийном клине конвективных валов, ориентированных поперек субдукции, как на рис. 4, характерно для достаточно малых углов субдукции. Так, при β = 30° поперечные валы не возникают [13]. В случае неньютоновской реологии поперечные валы (2D конвективные вихри Карига) могут возникать и при бóльших углах субдукции и достаточно малых скоростях субдукции. Очевидно, наличие двумерной конвекции в узком мантийном клине связано с бóльшими, чем в широком клине, вязкими напряжениями и, следовательно, с бóльшим диссипативным нагревом. Для неньютоновской реологии мантии конвекция при V = 20 мм×год-1 возникает при концентрации воды Сw ~ 1 весовых % благодаря формированию двух невозмущенных вынужденных течений, расположенных одно над другим, и значительному вязкому трению верхнего вынужденного течения, движущегося навстречу субдуцирующей литосферной плите. Следует отметить, что в многочисленных исследованиях термомеханического состояния мантии в зонах субдукции (см., например, [14] и обширную библиографию в этих статьях) не получалось конвекции в виде валов, поперечных к направлению субдукции, так как модели с неньютоновской реологией в мантийном клине не рассматривались, хотя именно в мантийном клине неньютоновская вязкость может играть доминирующую роль, так как сильно понижается благодаря воде, «выжимаемой» из субдуцирующего блока. Действительно, понижение эффективной вязкости мантии из-за наличия воды происходит только в случае неньютоновской реологии. Подчеркнем, что течение, индуцируемое в мантийном клине субдуцирующей литосферной плитой и не возмущенное конвекцией, состоит из двух расположенных одно над другим течений «А» и «В» (рис. 3) только в случает неньютоновской реологии мантии, и именно в этом случает формируется локализованная зона трения в области контакта встречного течения «А» и субдуцирующей литосферной плиты. В этой зоне велико диссипативное тепловыделение, порождающее восходящий конвективный поток (показанный вектором q на рис. 4 (2)). Кроме тепла, этот поток может выносить к поверхности Земли металлические руды и способствовать формированию залежей железа и других металлов. В Пакистанской части зоны субдукции Макран пониженный тепловой поток в тылу зоны субдукции может объясняться повышением содержания воды до 2 весовых % и уменьшением энергии активации на 40 кДж·моль– 1 по сравнению с Иранской частью или альтернативным повышением содержания воды до 1,5 весовых % и уменьшением энергии активации на 45 кДж·моль– 1. Считается общепринятым, что с ростом «влажности» среды энергия активации слагающих пород уменьшается, хотя формул, связывающих энергию активации с концентрацией воды не существует. Предлагаемая модель показывает, насколько по величине аномального теплового потока можно оценить уменьшение энергии активации с ростом содержания воды.
Выводы
В случае неньютоновской реологии характерный размер конвективной ячейки, полученной в модели мантийного клина, сформировавшегося при субдукции океанической части Аравийской литосферной плиты под Евроазиатскую литосферную плиту, составляет ~ 200 км, что при скорости субдукции 20 мм в год практически точно совпадает с характерным пространственным размером 2D-аномалии теплового потока широтного простирания на Иранском плато при ~ 33ºN в тылу зоны субдукции Макран. Локализация восходящего 2D конвективного потока в предлагаемой модели также соответствует расположению наблюдаемой зоны повышенного теплового потока на широте ~ 33ºN. В тылу Пакистанской части зоны субдукции Макран тепловой поток меньше, чем в Иранской части, что, по-видимому, можно объяснить прерывистым режимом субдукции, происходящей в ходе последовательности сильных землетрясений, связанным с этим ростом содержания воды и уменьшением на 40 кДж·моль– 1 энергии активации материала мантийного клина. Подъем конвективного потока, восходящего из мантийного клина в направлении к дневной поверхности, может выносить мантийные углеводороды и металлосодержащие геофлюиды и способствовать формированию нефтегазоносного района и залежей металлических руд в областях повышенного теплового потока.
Литература
1. Penney C., Tavakoli F., Saadat A., Nankali H.R., Sedighi M., Khorrami F., Sobouti F., Rafi Z., Copley A., Jackson J., Priestley K. Megathrust and accretionary wedge properties and behavior in the Makran subduction zone // Geophysical Journal International. 2017. V. 209. Р. 1800–1830. DOI: 10.1093/gji/ggx126.
2. Mousavi N., Ebrahimzadeh A.V. 3D Surface Heat Flow, Low-Temperature Basins and Curie Point Depth of the Iranian Plateau: Hydrocarbon Reservoirs and Iron Deposits // Journal of the Earth and Space Physics. 2023. V. 48. No. 4. P. 137-150. DOI: http//doi.org/10.22059/jesphys.2023.348000.1007453.
3. Гаврилов С.В., Харитонов А.Л. Геодинамическое моделирование глубинного строения и процессов конвективного выноса УВ из мантийного клина в тылу зоны субдукции Макран для поисков нефтегазовых месторождений на территории Ирана // Геология, география и глобальная энергия. 2024. № 2 (93). С. 19–28.
4. Жарков В.Н. Физика земных недр. М.: Наука и просвещение. 2012. 384 с.
5. Gao, X., Wang, K. Strength of stick-slip and creeping subduction megathrusts from heat flow observations. Science. 2014. № 345 (620). P. 1038–1041. DOI:10.1126/science.1255487.
6. Schubert G., Turcotte D.L., Olson P. Mantle Convection in the Earth and Planets. New York: Cambridge University Press, 2001. 940 p.
7. Гаврилов С.В., Харитонов А.Л. Оценка скорости субдукции Русской платформы под Сибирскую в палеозое по распределению зон выноса мантийных углеводородов в Западной Сибири // Геофизические Исследования. 2015. Т. 16. № 4. С. 36–40.
8. Billen M., Hirth G. Newtonian versus non-Newtonian Upper Mantle Viscosity: Implications for Subduction Initiation // Geophys. Res. Lett. 2005. V. 32. (L19304). DOI:10.1029/2005GL023458.
9. Жарков В.Н. Геофизические исследования планет и спутников. М.:ИФЗ РАН. 2003. 102 с.
10. Трубицын В.П. Реология мантии и тектоника океанических литосферных плит // Физика Земли. 2012. № 6. С. 3–22.
11. Трубицын В.П., Трубицын А.П. Численная модель образования совокупности литосферных плит и их прохождения через границу 660 км // Физика Земли. 2014. № 6. С. 138–147.
12. Gerya T.V. Future directions in subduction modeling // J. of Geodynamics. 2011. V.52. P. 344–378.
13. Гаврилов С.В., Абботт Д.Х. Термомеханическая модель тепло- и массопереноса в окрестности зоны субдукции // Физика Земли. 1999. № 12. С. 3–12.
14. Gerya T.V., Connolly J.A.D., Yuen D.A., Gorczyk W., Cape A.M.l. Seismic implications of mantle wedge plumes // Phys. Earth Planet. Inter. 2006. V. 156. P. 59–74.