Важным звеном моделирования газотранспортной системы является программный комплекс (ПК) расчета течения газовой смеси по линейной части газопровода. Этот программный комплекс включает в себя:
1) программу расчета штатных (без утечки) установившихся и неустановившихся режимов течения;
2) программу расчета коэффициента гидравлического сопротивления и суммарного коэффициента теплопередачи в рассматриваемой задаче по экспериментальным данным, соответствующим штатному режиму течения в моделируемом газопроводе (использование рассчитанных величин увеличивает адекватность модели);
3) программу расчета нештатных неустановившихся и установившихся режимов при утечке газа, вызванной разгерметизацией газопровода.
Программные комплексы 1-го и 2-го пунктов входят в состав разработанных нами ранее ПК «ТранSшельф-t» и «ТранSшельф-rev», описанных в работах [1, 2].
В книге [1] приведены примеры идентификации параметров и , а также результаты расчетов неустановившихся течений по морским газопроводам, в том числе и при оледенении их внешней поверхности в северных морях по ПК «ТранSшельф-t».
В настоящей работе представлен программный комплекс «ТранS-APL», позволяющий рассчитать неустановившиеся и установившиеся режимы при утечке газа средней и малой интенсивности в газопроводах средних давлений (до 100 атм).
Модель 1 нестационарного течения в газопроводах
Как известно [3, 1], сравнительно общая одномерная нестационарная модель течения смеси газов в терминах величин, осредненных по сечению газопровода, может быть записана следующим образом:
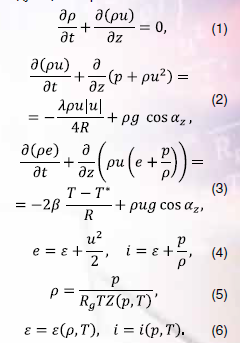
Эта модель эквивалентна модели, в которой вместо уравнения полной энергии (3) используется уравнение баланса энтальпии ( ), записанное в терминах температуры:
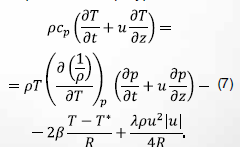
В уравнениях (1)–(7) приняты следующие обозначения: – время; – координата вдоль оси газопровода; – плотность, давление, температура и скорость газа; – массовые плотности внутренней энергии, полной энергии и энтальпии газа соответственно; – внутренний радиус газопровода; – ускорение свободного падения; – угол между направлением силы тяжести и осью газопровода в -м сечении; – коэффициент гидравлического сопротивления; – суммарный коэффициент теплопередачи; – температура окружающей среды; – газовая постоянная транспортируемой смеси газов; – коэффициент сжимаемости газовой смеси; – удельная изобарная теплоемкость газовой смеси.
Адекватность математической модели в каждой реальной задаче транспортировки газа достигается выбором следующих величин (или их зависимостей от параметров потока и конструкции газопровода): .
Предложено немало полуэмпирических зависимостей для расчета перечисленных величин, они базируются на обработке обширного экспериментального материала, например работы [4, 5]. Однако такие параметры, как коэффициент гидравлического сопротивления и суммарный коэффициент теплопередачи, надежнее всего определять на рассматриваемом участке газопровода из решения обратной задачи, реализованной в программе «ТранSшельф-rev» [1].
При тестовых расчетах различных режимов течения в исследовательских целях в математической модели могут использоваться известные зависимости, например – формула Колбрука–Уайта для расчета зависимости от числа Рейнольдса и эквивалентной шероховатости внутренней поверхности газопровода, зависимость Бертло для коэффициента сжимаемости , если давления не превышают 100 атм и т.п.
Модель 2 установившегося течения в штатном режиме для горизонтальных трасс
Для давлений на входе, не превышающих 100 атм при установившемся режиме течения (без утечки) для горизонтальных трасс прокладки газопровода, модель 1 (уравнения (1), (2), (7), (5)) переходит в модель 2.б:
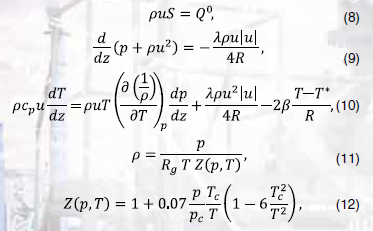
– постоянный массовый расход газа; – критические давление и температура газовой смеси, входящие в уравнение Бертло (12). Как показано, например, в работе [6], для уравнения Бертло зависимость удельной изобарной теплоемкости от давления и температуры имеет вид:
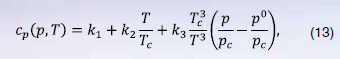
– давление, при котором смесь газов заданного состава ведет себя как идеальный газ; величины размерных констант зависят от состава газовой смеси, их расчет приведен в [6]. В ряде задач допустимо использование постоянного среднего значения , рассчитываемого по формуле
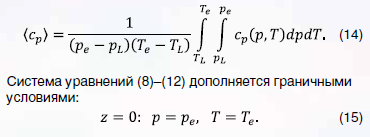
В (14) и (15) обозначено: – давление и температура газа на входе и на выходе из газопровода соответственно.
Вводятся безразмерные величины, определенные равенствами:
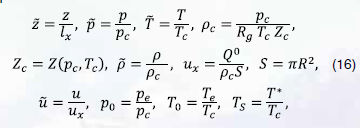
– характерная длина.
Далее везде, где это не приводит к двусмысленности, указание волны у безразмерных величин опущено. Модель 2 в безразмерной форме может быть представлена следующим образом: (модель 2.б)

Безразмерные комплексы , входящие в модель 2.б, выражаются через характерные величины и параметры задачи по формулам:
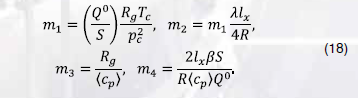
Решение системы уравнений модели 2.б в широком диапазоне изменений условий на входе , расхода , геометрических параметров газопровода существует и единственно. Оно находится следующим образом: система уравнений разрешается относительно первых производных давления и температуры по и интегрируется при заданных граничных условиях (17) численно, например методом Рунге–Кутты 4-го порядка точности.
Модель установившегося течения в газопроводе при утечке газа
При возникновении малой (средней) стационарной утечки в сечении с размерной координатой спустя некоторое время в газопроводе может установиться новый стационарный режим, в котором для расхода справедливо равенство:
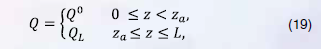
– длина газопровода. Разность определяет размер утечки.
Прямая задача расчета давления, температуры, плотности и скорости газа в новом установившемся режиме при известных величине и координате утечки газа решается численным интегрированием системы уравнений модели 2.б для двух участков:
. Здесь – безразмерная координата места утечки газа.
На первом участке в области система уравнений модели 2.б решается при граничных условиях (17) с безразмерными комплексами (18), рассчитанными при постоянном расходе . На втором участке в области система уравнений модели 2.б решается при граничных условиях:
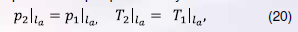
в которых величины рассчитаны на первом участке. Безразмерные комплексы (18) для второго участка рассчитываются при постоянном расходе .
Обратная задача. Алгоритм расчета места и величины утечки газа по данным о величинах массового расхода и давления на выходе из газопровода приведен в наших работах: для средних давлений (менее 100 атм) в работе [7], для сверхвысоких давлений (более 200 атм) – в работе [8]. Алгоритм основан на итерационном методе идентификации параметра , который применительно к течениям в скважине предложен в работе [3], при этом дополнительно на каждой итерации используется линейность зависимости давления и температуры от искомой координаты места утечки (линейность доказана в наших работах для широкого диапазона изменений давления и расхода непосредственными расчетами по прямой задаче). Анализ различных вариантов выбора начального приближения в итерационном процессе показал, что наибольшую точность расчета и максимальную скорость сходимости итерационного процесса обеспечивает задание начального приближения, рассчитанного по упрощенной изотермической (или упрощенной неизотермической) модели [9].
Представленный в работах [7, 8] алгоритм решения обратной задачи прост в реализации. Он позволяет с высокой точностью за несколько минут рассчитать на компьютере средней мощности величину и координату места утечки газа по данным о давлении и расходе на выходе из газопровода. На практике точность расчета лимитируется точностью измерительной аппаратуры. Кроме того, предложенное решение обратной задачи расчета места утечки справедливо лишь после установления в газопроводе нового стационарного режима.
Модель неустановившегося течения в газопроводе при утечке газа
Возникновение утечки газа приводит к неустановившемуся течению в газопроводе, причем время выхода на новый установившийся режим течения может оказаться немалым. Для оперативного обнаружения модельными методами утечки газа малой и средней интенсивности необходимы решения прямой и обратной задач по модели неустановившегося течения, обусловленного возникновением утечки газа.
Нестационарная модель 1 в терминах удельного расхода , температуры , давления и плотности газа для горизонтальных трасс вне области утечки принимает вид (модель 1.1):
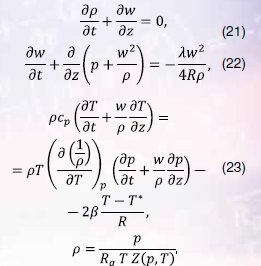
В окрестности сечения газопровода (с координатой ), содержащего локальную утечку газа кг/с, в уравнение неразрывности (21) добавляется слагаемое, моделирующее сток газа, а именно, при уравнение неразрывности записывается в виде:
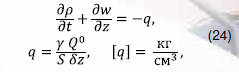
здесь – относительная величина утечки, – площадь поперечного сечения, – ширина переходного слоя, приближенно заменяющего поверхность разрыва удельного расхода. Выбор величины при численном решении системы уравнений зависит от относительной величины утечки и, кроме того, от параметров расчетной сетки численного решения. Анализ выбора величины для задач газовой динамики содержится, например, в работе [10].
Упрощенная модель неустановившегося течения в газопроводе
Решения многочисленных задач по идентификации координаты утечки газа в установившихся режимах [6, 9] свидетельствуют о том, что во многих случаях, когда изменение температуры газа составляет несколько градусов, можно ограничиться для расчета координаты утечки изотермическим приближением. Похожее заключение приведено, например, в книге С.А. Коршунова [11]: «…численные расчеты продемонстрировали большую инертность определяемых параметров утечки от температуры…». В качестве постоянных значений температуры и коэффициента сжимаемости в изотермической модели естественно использовать их средние величины, вычисленные по соответствующей неизотермической модели 2.
Другое допустимое упрощение модели связано с пренебрежимо малой величиной сил инерции по сравнению с давлением в потоке, характерной для большинства задач транспортировки газа. Например, для давления атм при температуре плотность смеси газов при Дж/(кг К), рассчитанная по уравнению состояния Бертло, равна . При массовом расходе газа 150 кг/с и при внутреннем радиусе газопровода м скорость потока составляет величину м/с. При этих параметрах отношение сил инерции к давлению равно безразмерной величине . Столь малая величина этого отношения характерна для большинства задач транспортировки газа.
С учетом сказанного модель 3.б – упрощенная модель неустановившегося течения в газопроводе – в безразмерной форме в терминах безразмерных давления , удельного расхода , плотности , времени и координаты может быть представлена в следующем виде (указание волны у безразмерных величин опущено):
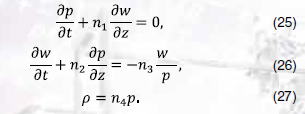
При приведении к безразмерному виду использованы те же характерные величины давления , плотности , скорости , что и в безразмерной модели 2.б; характерные удельный расход и время определены равенствами: , .
Здесь – средняя адиабатическая скорость звука в газе, равная:
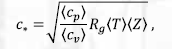
– отношение средних удельных теплоемкостей газовой смеси при постоянном давлении и постоянном объеме, , – средние температура и коэффициент сжимаемости, рассчитанные по неизотермической модели 2.
Безразмерные комплексы модели 3.б вычисляются по формулам:
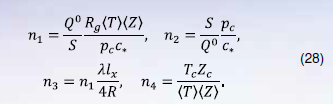
В окрестности сечения газопровода (с безразмерной координатой ), содержащего локальную утечку газа, размерное уравнение (24) со слагаемым, моделирующим сток газа, в безразмерном виде для принятых характерных величин в терминах давления и удельного расхода преобразуется в следующее уравнение:
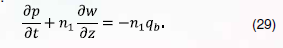
Краевые условия для системы уравнений модели 3.б
Если до возникновения утечки газа штатный режим течения был установившимся, то в качестве начальных условий при для нестационарной изотермической модели 3.б задаются следующие начальные условия: постоянство удельного расхода вдоль газопровода и распределение давления, рассчитанное по изотермическому приближению модели 2. В безразмерной форме эти условия имеют в вид:
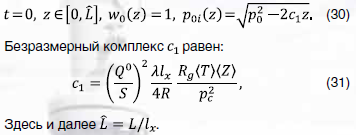
Задание граничных условий для квазилинейной гиперболической системы уравнений (25–27), которые обеспечили бы существование и единственность ее решения, как известно [12], не может быть произвольным. В рассматриваемом круге задач скорость потока положительная и дозвуковая, поэтому на входе в газопровод и на выходе из него должна быть задана одна и только одна из функций – либо давление , либо удельный расход . Рассматривались разные варианты задания граничных условий.
В настоящей работе приведены примеры решения системы уравнений (25–27) при возникновении утечки малой и средней интенсивности при следующих вариантах задания давления на входе и на выходе: 1) ; 2) ,
Линеаризация модели неустановившегося течения
В работе [13] предложена линеаризация уравнения баланса импульса (26), основанная на замене нелинейного слагаемого в правой части размерного варианта этого уравнения линейным слагаемым:
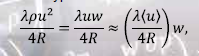
здесь – средняя скорость потока. Безразмерное линеаризованное уравнение баланса импульса (26) принимает вид (волна у безразмерных величин опущена):
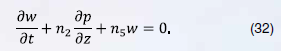
Безразмерный комплекс равен:
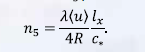
Линеаризованная система уравнений (25), (32), (27) для некоторых вариантов краевых условий допускает аналитическое решение, полученное в работе [13]. Не умаляя ценности аналитического решения для тестирования предлагаемых методов численного решения, отметим следующее. Для ряда характерных параметров задачи транспортировки газа (например, приведенных далее (33)) расчет по исходной системе уравнений (25–27) существенно отличается от расчета по линеаризованной системе (25), (32), (27), поэтому в расчетах использовалась нелинейная модель неустановившегося течения в газопроводе (25–27).
Численное решение системы уравнений модели неустановившегося течения при возникновении утечки газа
Опыт решения нестационарных неизотермических задач о течениях в газопроводах средних и сверхвысоких давлений [1] свидетельствует о том, что для численного решения этих задач может быть использована модифицированная явная двухшаговая схема Лакса–Вендроффа, которая имеет второй порядок точности по и по в области гладкости решения и требует соблюдения ограничения на величину шага по времени, следующего из критерия Куранта–Фридрихса–Леви. Как известно, схемы типа Лакса–Вендроффа просты в реализации, экономичны и допускают распараллеливание. Известным недостатком этих схем является немонотонность, проявляющаяся в появлении нефизических осцилляций численного решения (особенно в области резких изменений сеточных функций), однако эти осцилляции проявляются в сравнительно узкой области и не приводят к неустойчивости счета. Во всех предыдущих расчетах по схеме типа Лакса–Вендроффа, приведенных в книге [1], осцилляции не вносили существенной погрешности в решение, т.к. их модуль был пренебрежимо мал по сравнению с абсолютной величиной рассчитываемых величин.
Известно большое количество монотонных численных схем решения квазилинейных гиперболических систем [12]. Все они имеют свои достоинства и недостатки, обзор и анализ этих схем содержится в книге [12]. В настоящей работе модифицированная схема Лакса–Вендроффа (алгоритм которой применительно к задачам транспортировки газа подробно описан в книге [1]) использовалась для численного решения системы уравнений (25–27) в области гладких решений, в области утечки газа вместо уравнения (25) на первом и на втором шагах схемы Лакса–Вендроффа использовалась численная аппроксимация уравнения (29), величины давления на границах области утечки полагались равными.
Примеры расчетов
Расчеты проводились по созданному ПК «ТранS-APL», включающему: 1) программу расчета неизотермических и изотермических установившихся течений как в штатном режиме, так и при наличии утечки малой и средней интенсивности при средних давлениях; 2) программу расчета при средних давлениях неустановившихся изотермических течений с заданной утечкой газа, основанную на модифицированной схеме Лакса–Вендроффа. Для тестовых расчетов использовался следующий набор неизменных параметров задачи:
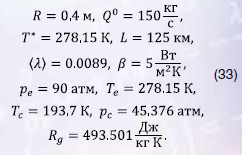
Критические температура и давление , а также газовая постоянная в (33) соответствуют смеси газов из 12 компонент с преобладанием метана [1].
Варьировались величина утечки и ее местоположение. Для системы уравнений (25–27) граничное условие на входе имело вид: , граничное условие на выходе из газопровода задавалось равенством: .
Поведение безразмерного давления на выходе из газопровода длиной 125 км рассчитывалось из решения соответствующей нестационарной задачи для газопровода длиной км с тем же граничным условием для безразмерного давления на входе но с постоянным граничным условием для безразмерного давления на выходе из газопровода: , . Величины новой длины газопровода и постоянного безразмерного давления на его конце определялись в результате численного эксперимента таким образом, чтобы при том же начальном условии (30), при той же утечке газа минимизировать зависимость функции от величины и обеспечить при в новом установившемся режиме при наличии заданной утечки выполнение условия:
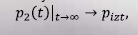
здесь – безразмерное давление, рассчитанное в сечении газопровода 125 км по модели изотермического установившегося течения при заданной утечке газа, равное:
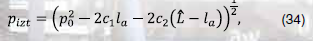
безразмерный комплекс определен равенством (31), безразмерный комплекс равен:
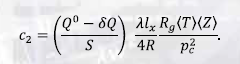
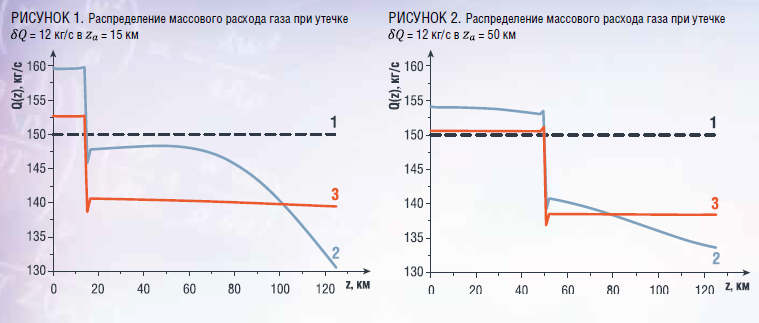
Примеры тестовых расчетов представлены на рис. 1–6. На рис. 1–3 приведены данные расчета распределений массового расхода вдоль газопровода при утечке газа с массовым расходом кг/с. Данные рис. 1 соответствуют утечке газа, расположенной в сечении с координатой км, данные рис. 2 – км, данные рис. 3 – км. На рис. 1–3 кривая «1» соответствует моменту времени t = 0 мин, кривая «2» – t = 10 мин, кривая «3» – t = 60 мин.
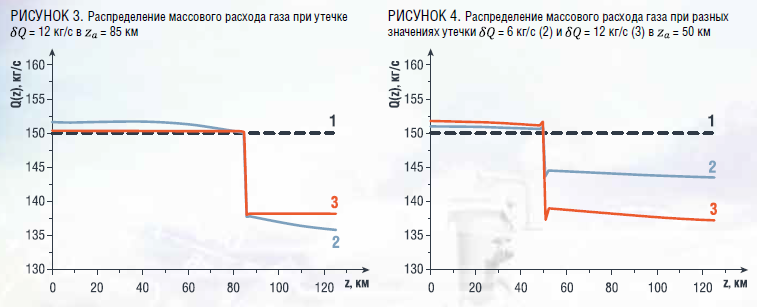
Рис. 4 иллюстрирует зависимость распределения массового расхода газа Q от интенсивности утечки (кривая «1» соответствует постоянному начальному расходу газа). Кривые «2» и «3» соответствуют моменту времени t = 25 мин, распределение массового расхода газа при утечке кг/с представлено кривой «3», при утечке кг/с – кривой «2».
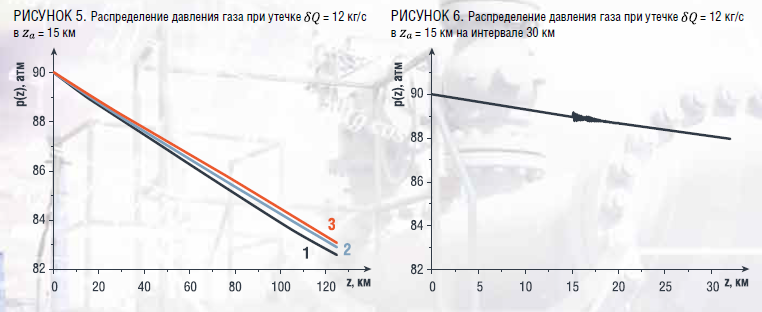
На рис. 5 приведены распределения давления p в газопроводе при утечке с массовым расходом кг/с в сечении с координатой км в разные моменты времени. Распределение давления «1» соответствует моменту времени t = 10 мин, распределение «2» – t = 25 мин, распределение «3» – t = 120 мин.
Рис. 6 служит иллюстрацией немонотонности величин, рассчитанных по модифицированной схеме Лакса–Вендроффа. Расчет представлен для утечки газа средней интенсивности с массовым расходом кг/с в сечении газопровода с координатой км. Масштаб по оси абсцисс на рис. 6 изменен с тем, чтобы осцилляции стали заметнее.
Из проведенных тестовых расчетов, часть из которых представлена на рис. 1–6, следует, что с течением времени профили распределений расхода газа стабилизируются как при малых утечках ( кг/с), так и при средних утечках ( кг/с) (при начальном массовом расходе газа, равном кг/с). Время стабилизации, как и следует ожидать, увеличивается с увеличением интенсивности утечки. Из рис. 5 видно, что распределение давления, а также его величина на конце газопровода относительно мало изменяются при малых и средних утечках газа. Из рис. 6 следует, что даже при утечках газа средней интенсивности величина осцилляций относительно незначительна и ее проявление ограничено небольшой областью.
Выводы
Для газопроводов средних давлений (до 100 атм) в работе представлен расчет по ПК «ТранS-APL» характеристик неустановившихся течений, возникающих в нештатных ситуациях, обусловленных появлением утечки газа.
Для широкого круга задач, представляющих практический интерес, обоснована допустимость использования упрощенной нестационарной модели течения при утечке малой или средней интенсивности.
Предложен экономичный и простой в реализации метод численного решения системы уравнений модели при наличии утечки. Метод основан на модифицированной схеме Лакса–Вендроффа. Приведенные примеры расчетов этим методом распределений давления и расхода в газопроводе при наличии утечек разной интенсивности и расположенных в разных местах газопровода демонстрируют допустимость использования явных схем, типа схем Лакса–Вендроффа, для рассмотренного круга задач.
Проведенное в работе исследование позволяет существенно упростить оперативное обнаружение места утечки газа. Решение этой задачи выходит за рамки настоящей статьи.
Предложенные нестационарная модель и метод численного решения системы уравнений модели допускают обобщение на газопроводы сверхвысоких давлений (свыше 200 атм) и на задачи, в которых необходим учет неизотермичности процессов.
Литература
1. Курбатова Г.И., Ермолаева Н.Н., Филиппов В.Б., Филиппов К.Б. Проектирование газопроводов в северных морях. Санкт-Петербург: Лань, – 2020. – 352 с.
2. Курбатова, Г.И., Клемешев, В.А. & Филиппов, К.Б. Цифровые модели подводных трубопроводов в северных морях. Деловой журнал «Neftegaz.RU». 2022. № 1 (121). С. 72–77.
3. Васильев О.Ф., Бондарев Э.А., Воеводин А.Ф., Каниболотский М.А. Неизотермическое течение газа в трубах. – Новосибирск: Наука СО, – 1978. – 128 с.
4. Сулейманов В.А. Некоторые вопросы термодинамики процесса трубопроводного транспорта природного газа // Повышение надежности и безопасности объектов газовой промышленности. 2022. № 2 (51). С. 29–45.
5. Лурье М.В. Теоретические основы трубопроводного транспорта нефти, нефтепродуктов и газа. М.: Недра, 2017. – 476 с.
6. Курбатова Г.И., Клемешев В.А., Егоров Н.В. О возможности использования упрощенных моделей для определения места утечки в газопроводе. Журнал технической физики, 2022. Том 92. Вып. 10. С. 1509–1516.
7. Курбатова Г.И., Клемешев В.А. Математический аппарат обнаружения места утечки в газопроводах. Математическое моделирование, 2021. 33 (8), с. 27–41.
8. Курбатова, Галина Ибрагимовна; Клемешев, Владимир Алексеевич. Идентификация места утечки газа малой и средней интенсивности в газопроводах средних и сверхвысоких давлений. Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. 2023. Том 19. № 2. C. 218–232.
9. Курбатова Г.И., Виноградова Е.М. & Клемешев В.А. Анализ упрощенных моделей транспортировки газа. расчет местоположения утечки газа в трубопроводе. Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. 2022. Т.18. Вып. 2, с. 239–252.
10. В.Ф. Куропатенко, И.Р. Макеева. Исследование дистракции разрывов в методах расчета ударных волн // Математическое моделирование. 2006. Т. 18. № 3. С. 120–128.
11. Коршунов С. Идентификация утечек газа. Магистральные газопроводы высокого давления. Саарбрюккен: Lambert Academic Publ., 2014. 218~с.
12. Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: ФИЗМАТЛИТ, 2012. 656 с.
13. Лаптева Т.И., Мансуров М.Н. Обнаружение утечек при неустановившемся течении в трубах // Нефтегазовое дело, 2, 1 (2006). [Электронный ресурс] – 28.04.2024.






