Совершенствование способа подсчета механических частиц в турбулентном потоке с использованием цифровых алгоритмов обработки видео

Ключевые слова: количественный анализ частиц, погрешности подсчета, механические частицы, турбулентный поток, цифровизация.

Количественный анализ частиц в жидких средах является неотъемлемой составляющей в различных отраслях промышленности от нефтехимии до фармацевтики. Необходимо учитывать, что постоянное совершенствование методов подсчета различных элементов является ключевым фактором для оптимизации производственных процессов и повышения качества продукции. Развитие и улучшение цифровых средств анализа позволяет повысить удобство проведения экспериментов и точность получаемых данных. Важность данной задачи подчеркивается результатами предыдущих исследований [1], где были представлены существующие методы подсчета частиц и разработана программа с удобным графическим интерфейсом.
Благодаря этой разработке возможно проводить анализ количества частиц и определять их скорость в потоке жидкости на основе видеозаписи экспериментов, что значительно ускоряет процесс проведения опытов и повышает точность результатов. Тем не менее следует отметить, что методика, описанная в вышеупомянутой статье, не лишена недостатков, и в процессе испытаний возникли определенные трудности.
Для успешной реализации разработки программы был выбран язык программирования Python. Важную роль в процессах обнаружения и обработки видео сыграли функции библиотеки OpenCv-python и алгоритм отслеживания DeepSORT из библиотеки deep-sortrealtime. Создание графического интерфейса было выполнено с применением Tkinter. Использование данных инструментов позволяет эффективно обрабатывать видео и отслеживать движущиеся объекты, что является важнейшим элементом в проекте по обнаружению частиц. Совместное применение различных технологий и алгоритмов позволяет добиться точности и надежности в работе программы.
Одним из основных вызовов при обнаружении частиц является возможное появление пузырьков воздуха в системе, которые воспринимаются как частицы, хотя на самом деле таковыми не являются. Также стоит отметить, что при наличии частиц, расположенных вблизи друг от друга, алгоритм обнаружения может идентифицировать их как один объект. Еще одним недостатком является сложность качественного распознавания частиц на темном фоне из-за слияния с ним или по причине изменений таких условий эксперимента, как уровень освещения или положение камеры.
Выявление объектов на видео – это сложный процесс, который включает в себя несколько этапов обработки изображения. Вначале применяется алгоритм разделения модели гауссовой смеси, который предшествует гауссовскому сглаживанию. Эти шаги необходимы для создания маски переднего плана. Для улучшения качества маски и удаления шумов и теней, применяется пороговая обработка, за которой следуют операции морфологического открытия и закрытия.
Далее, для дополнительной обработки маски переднего плана, применяется операция преобразования дистанции, которая позволяет определить расстояние от каждого пикселя до ближайшего объекта. После этого снова выполняется пороговая обработка, где пороговое значение устанавливается как максимальное значение карты преобразования дистанции, умноженное на коэффициент

Эти шаги позволяют точнее выделить объекты на видео и улучшить качество детектирования. Каждая операция в цепочке обработки имеет свою роль и важность для достижения оптимальных результатов в распознавании объектов на видео.
Для правильного выделения частиц на карте сегментации необходимо выполнить операцию преобразования дистанции, которая заключается в определении расстояния между каждым ненулевым пикселем и ближайшим нулевым. Этот этап преобразования играет решающую роль в разделении близко расположенных частиц на отдельные объекты.
Большим преимуществом данной программы является высокая скорость работы, что позволяет проводить анализ и обработку данных быстро и эффективно. Кроме того, программа дает возможность использовать любые расположения камеры благодаря алгоритму вычитания фона, который фокусируется исключительно на движущихся объектах, игнорируя ненужные детали из видеопотока.
Важно отметить, что выбор контура является неотъемлемой частью процесса обработки изображений и видео для выделения объектов интереса. Этот метод позволяет улучшить точность сегментации и обеспечить более четкую и надежную идентификацию объектов на изображениях.
В контексте описанной программы важно обратить внимание на недостатки, которые могут повлиять на точность результатов. Один из таких недостатков заключается в отсутствии учета максимально допустимых погрешностей при подсчете задержавшихся частиц, особенно в связи с применяемой методикой. Это может привести к искажению данных и неверным выводам.
В результате для достоверной оценки результатов и избежания искажений, необходимо уделить особое внимание анализу и коррекции недочетов в программе. Это позволит повысить достоверность результатов и улучшить качество проводимых исследований.

Также следует отметить, что распределение количества частиц в программе не соответствует ни нормальному распределению, ни какому-либо другому известному распределению (см. рисунок 1). Это означает, что стандартные методы оценки, основанные на статистике или максимальных значениях, могут оказаться неэффективными или даже ошибочными. Однако, несмотря на упомянутый недостаток, данный метод подсчета частиц является робастным. Это значит, что вероятность учета как частицы любых других движущихся (например, движение трубы) объектов меньше. Тестирование данного метода на видео с экспериментами, в которых прошлая программа выдавала некорректные значения (задержавшихся частиц больше, чем частиц в системе), прошло успешно. Результаты работы программы являются адекватными. Также стоит отметить, что была увеличена производительность.

Погрешности являются неотъемлемой частью любых экспериментальных исследований и должны быть тщательно учтены при проведении научных работ. Какими бы точными и совершенными ни были средства и методы измерения и как бы тщательно ни выполнялись сами измерения, их результат всегда отличается от истинного значения измеряемой физической величины, т.е. обладает некоторой погрешностью.

Источниками погрешностей являются:

- несовершенство применяемых методов и средств измерений;

- непостоянство влияющих на результат измерения физических величин;

- индивидуальные особенности экспериментатора [2].

Существует множество способов систематизации, которые позволяют детально анализировать источники и характер погрешностей. Например, в работе [3] предложена новая классификация. Понимание природы погрешностей, методов их оценки и учета – это важный аспект получения достоверных результатов экспериментальных исследований в различных областях науки и техники.

Также в зависимости от источника возникновения различают три основных вида погрешностей: инструментальные, методические и субъективные.
Инструментальные погрешности связаны с ограниченной точностью применяемых средств измерений. Это могут быть погрешности показаний, округления характеристик используемых приборов.
Методические погрешности обусловлены несовершенством самой методики проведения измерений. Они возникают, если принятая модель объекта измерения не в полной мере соответствует реальному объекту. Например, при измерении площади поперечного сечения детали, если считать его идеально круглым, в то время как форма может существенно отличаться. Методические погрешности могут также появляться из-за влияния средств измерений на объект (например, подключение вольтметра к электрической цепи) или погрешностей вычислительных алгоритмов.

Субъективные погрешности связаны с человеческим фактором – неточностью отсчета показаний оператором, влиянием его состояния, несовершенством органов чувств. Применение автоматизированных измерительных систем позволяет свести к минимуму такого рода погрешности [4].

Для оценки погрешности подсчета частиц в данном проекте принята гипотеза о том, что отсутствуют аддитивная и мультипликативная погрешности. Истинное количество частиц определяется как среднее количество прошедших через экспериментальный участок частиц:

где 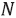– оценка количества частиц, подсчитанных во время проведения эксперимента;

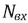– количество частиц, прошедших через камеру, стоящую на входе в экспериментальный участок (таблица 1);

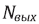– количество частиц, прошедших через камеру, стоящую на выходе из экспериментального участка (таблица 2).

Измеряется количество частиц на входе и выходе эксперимента для оценки погрешности программы и рассчитывается абсолютная (2) и относительная (3) погрешность. Для оценки математического ожидания определяется среднее значение погрешностей для всех экспериментов (таблица 3):

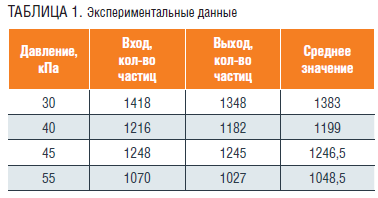
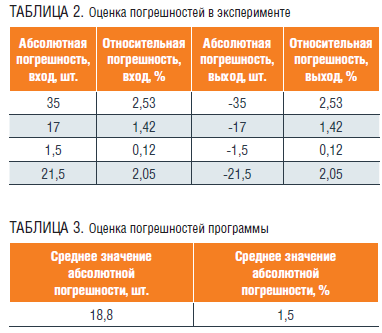
Программа обнаруживает частицу с точностью 1,5 %, что означает вероятность правильного обнаружения 98,5 %.

Погрешность подсчета частиц в результате эксперимента

С целью оценки погрешности количества частиц в эксперименте можно выписать следующее уравнение:

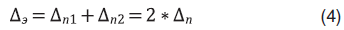
где 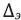– абсолютная погрешность подсчета количества частиц в эксперименте;
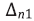– абсолютная погрешность подсчета количества частиц в эксперимент программой для камеры на входе в экспериментальную зону;
– абсолютная погрешность подсчета количества частиц в эксперимент программой для камеры на выходе из экспериментальной зоны;
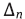– абсолютная погрешность подсчета количества частиц в эксперимент программой.

Формула расчета абсолютной погрешности:

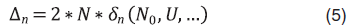
где 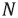– количество частиц, прошедших через экспериментальный участок;
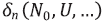– относительная погрешность программы;
– количество частиц, находящихся в экспериментальной установке;
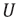– скорость движения частиц.

Погрешность подсчета частиц в эксперименте зависит от количества частиц в установке.

Погрешность программы зависит от скорости частиц. Влияют и другие параметры, невозможные для формального описания. Установив постоянное количество частиц, можно перейти к относительным погрешностям:

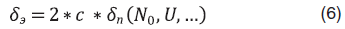
где 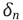– относительная погрешность подсчета частиц в эксперименте.

Формула (7) позволяет рассчитать погрешность подсчета частиц. Положим, с = 6, что приблизительно соответствует количеству кругов, которые частицы прошли во время эксперимента (так как , значение (таблица 3), тогда погрешность составляет 18 % (8).

Погрешность накапливается в ходе эксперимента, поэтому уменьшение количества кругов поможет минимизировать ее. Необходимо минимизировать время и количество частиц в эксперименте для уменьшения погрешности. Освещение, завихрения и другие факторы также влияют на точность измерений. Из формулы (7) видно, что погрешность работы программы накапливается по ходу эксперимента.

Оценка подсчета скорости частиц с помощью программы

Коэффициент корреляции Пирсона используется для оценки соответствия скорости частиц реальности.
Эксперимент с постоянным временем (60 секунд) показал, что количество частиц, прошедших через зону, зависит от скорости частиц. Однако корреляция между скоростью и давлением оказалась неожиданной (таблица 4). Возможно, давление указано неверно или зависимость скорости от давления не соответствует ожиданиям.

Таблица 4. Результаты корреляционного анализа

Результат корреляционного анализа можно подтвердить, проведя визуальную оценку видеозаписи экспериментов. Расстояние между камерой и трубой в каждом эксперименте было равно 10 сантиметрам. Это означает, что более быстрое движение частиц соответствует большей скорости прохождения частиц по трубе, так как расстояние, проходимое частицами, является одинаковым для всех экспериментов. В результате визуальной оценки можно сделать вывод о том, что данные корреляционного анализа верны.

Заключение

Цель данного исследования заключалась в совершенствовании программы для подсчета механических частиц в потоке жидкости, а также в уменьшении погрешности в ее работе. Важно отметить, что достижение идеального уровня погрешности невозможно, поскольку на этот процесс влияет множество факторов. Тем не менее в результате проведенной работы были сформированы выводы, которые помогут минимизировать погрешность экспериментов и повысить точность подсчета частиц.

При этом стоит отметить, что еще на первых этапах проведения исследования предпринимались меры, исключающие влияние многих внешних факторов: недостаточная освещенность рабочего поля лабораторного стенда, характеристики используемой камеры и др. Подобные меры позволили сконцентрироваться непосредственно на вопросе погрешности работы программного обеспечения.

В ходе исследования были выявлены зависимости, указывающие на пути снижения значения погрешности, такие как минимизация времени и количества частиц. Кроме того, на входе в экспериментальную зону наблюдается значительные турбулентность, что приводит к ухудшению результатов подсчета частиц.

С учетом этих зависимостей были предприняты соответствующие действия, в том числе и по корректировке функций программного обеспечения, что позволило заметно снизить значение погрешности.

Активное развитие искусственного интеллекта и его применение в различных отраслях, включая системы анализа данных, дают возможность интеграции современных алгоритмов и методов в дальнейшее улучшение работы программы. Это позволит не только повысить точность и надежность существующих методов, но и открыть новые перспективы для исследований. Внедрение таких технологий способствует созданию более эффективных и высокопроизводительных систем, которые будут учитывать сложные факторы, влияющие на процесс подсчета. Таким образом, проведенная работа подчеркивает важность включения новых технологий в традиционные методы, что в конечном итоге приведет к повышению качества научных экспериментов и практических приложений.

Литература

1. Антонов С.В., Аверина Ю.М., Замрий А.В., Папушкина А.А., Негробов В.А., Зубарев Т.М. Способ подсчета механических частиц в потоке жидкости с использованием цифровых алгоритмов обработки видео [Журнал]. – Москва: Межотраслевой бюллетень МЭАЦ СНГПР, 2024 г.

2. Миронычев, В.Н. Метрология, стандартизация и сертификация [Электронный ресурс]: учебное электронное издание: учебное пособие для вузов / В.Н. Миронычев, П.Л. Титов; М-во образования и науки Российской Федерации, Дальневосточный федеральный ун-т, Инженерная шк. – Владивосток: ДВФУ, 2015. – 1 электрон. опт. диск (CD-ROM); 12 см; ISBN 978-5-7444-3561-5: 50 экз.

3. Ершова, И.Г. Погрешности измерений и их оценка / И.Г. Ершова // Вестник Псковского Государственного Университета. Серия: Экономика. Право. Управление. – 2012. – № 1. – С. 255.

4. Степанова, Е.А. Метрология и измерительная техника: основы обработки результатов измерений: учебное пособие для вузов / Е.А. Степанова, Н.А. Скулкина, А.С. Волегов; под общей редакцией Е.А. Степановой – Москва: Издательство Юрайт, 2024. – 95 с. – (Высшее образование). – ISBN 978-5-534-18065-7. – Текст: электронный // Образовательная платформа Юрайт. (дата обращения: 11.10.2024)