Автоматизация процесса ректификации представляет собой сложную практическую задачу вследствие большого числа различных взаимосвязанных параметров, со сложной и недостаточно изученной динамикой процесса. К тому же ректификационная колонна - объект управления со значительной инерционностью и временем запаздывания по каналам управления [1].
Сегодня значительно расширились возможности автоматизации, контроля и регулирования процесса ректификации. Использование контроллеров и SCADA-системы в качестве центрального управляющего органа позволяет учесть более широкий спектр технологических требований и повысить надежность поддержания оптимального технологического режима.
Целью исследования была задача создания системы оптимального управления ректификацией с использованием математической модели процесса, полностью компенсирующей возмущающие воздействия [2] и дальнейшее моделирование процесса с использованием SCADA-системы на лабораторной установке. Целью управления является поддержание заданного состава целевого продукта.
Анализ технологического процесса как объекта управления
Основными регулируемыми технологическими величинами являются составы дистиллята, кубового остатка. На чистоту этих целевых продуктов оказывает влияние ряд возмущающих воздействий процесса - состав сырья, давление в колонне, а так же другие величины [3].
Основные управляющие воздействия - расходы флегмы в колонну и температура термостата. Причем изменение расхода флегмы относительно быстро приводит к изменению состава дистиллята и одновременно с большим запаздыванием и в значительно меньшей степени - к изменению состава кубового остатка. Изменение же температуры термостата приводит в основном к изменению состава кубового остатка; состав флегмы при этом изменяется намного слабее.
Применительно к непрерывному процессу ректификации поддержание заданного по технологическому регламенту состава целевого потока является целью управления процессом. Состав потока, не содержащего целевого продукта, может меняться в определенных пределах вследствие изменения состава и скорости подачи исходного питающего потока. Возмущения по составу и расходу питающей смеси приводят к изменению давления, температуры, состава жидкости и паров в колонне. Но эти возмущения являются контролируемыми и могут быть учтены при реализации задач оптимального управления.
Наиболее сложным случаем управления ректификационной установкой является случай, когда целевыми потоками являются как поток дистиллята, так и поток кубовой жидкости. В таком случае требуется поддерживать заданный состав обоих потоков, а воздействие на состав кубовой жидкости или косвенно на ее температуру приводит к возмущению состава дистиллята через изменение температуры термостата, наоборот, воздействие на расход флегмы с целью стабилизации состава дистиллята влияет на состав кубовой жидкости. Взаимное влияние управляющих воздействий по обоим каналам на управляемые параметры вызывает дестабилизацию режима работы ректификационной колонны [6].
Трудности в одновременной стабилизации состава кубовой жидкости и дистиллята могут быть преодолены двумя способами. Первый способ состоит в автономном регулировании обоих параметров путем воздействия не только по основному каналу регулирования, например изменением температуры термостата, но и компенсируя возмущение по перекрестному каналу, например изменением расхода флегмы. Настроить такие контуры регулирования при соблюдении полной автономности довольно трудно. Второй способ состоит в управлении по возмущению с использованием математической модели тарельчатой ректификационной колонны. Технологическая схема лабораторной установки разработана в SCADA-системе GENESIS32 и представлена на рис. 1.
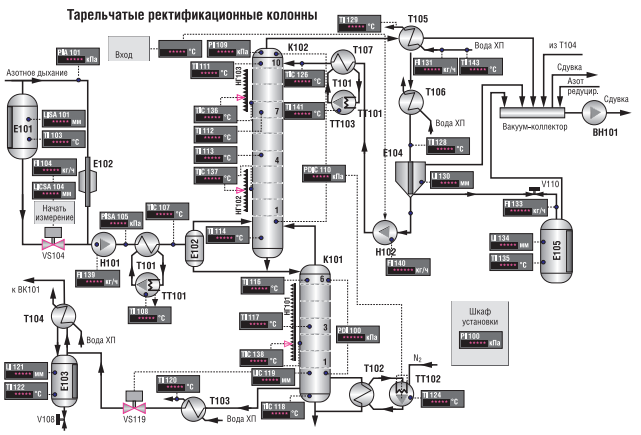
Рис. 1. Технологическая схема тарельчатых ректификационных колонн
Основные обозначения (рис. 1): K101 - K102 - ректификационная колонны, ТТ101 - ТТ102 - термостаты, Т101-Т107 - дефлегматоры; H101-H102 насосы, FI140, FI139, FL133 - датчики расхода флегмы, расхода исходной смеси, расхода дистелята соответственно, E101 – E105 – емкости для сбора технологических жидкостей, LI121 –уровень кубовой жидкости.
Управление предполагается вести следующим образом. Датчики расхода (FL139 на насосе H201) и значение состава QT (полученное в данной работе на аналитическом оборудовании) питающего потока (эти величины являются основными возмущающими воздействиями) измеряют текущие значения технологических параметров. Унифицированный выходной сигнал с датчика поступает на аналоговый вход контроллера. Значение аналогового сигнала преобразуется в цифровой код, а затем в значение технологического параметра. Для измеренных текущих значений расхода и состава питающего потока с помощью математической модели рассчитывается температура на термостате и расход флегмы (управляющие воздействия), при которых обеспечиваются требуемые составы кубовой жидкости в емкость Е103 и дистиллята в Е105. Требуемый расход флегмы выдается в качестве задания насосу H102 расхода флегмы, а требуемое значение температуры на термостат ТТ102.
Показателями качества управления могут быть такие свойства системы управления, как, например, точность поддержания заданного режима работы объекта управления, время достижения цели управления, значение максимальной ошибки в определенном режиме функционирования, надежность безотказной работы, производительность и качество выпускаемой продукции, затраты сырья или электроэнергии, себестоимость продукции, мощность используемого оборудования и т.д. Конкретизация обобщенного показателя качества в общей теории оптимальных систем не осуществляется и проводится в каждой частной задаче индивидуально. Наиболее часто обобщенный показатель качества представляет функционал, и его можно описать в форме интегрального соотношения [8]:
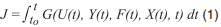
где U(t) - управление, Y(t) - управляемый процесс, F(t) - возмущения, X(t) - задающее воздействие, t - время.
Функция G определяет конкретный физический смысл показателя качества. Введение показателя (1) позволяет сформулировать задачу оптимального управления.
Задача оптимального управления заключается в следующем: в области допустимых управлений Ω(U) следует найти такое допустимое управление U(t), при котором показатель качества (1) при заданных F(t), X(t) достигает экстремального значения:
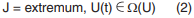
а объект управления переводится из начального состояния Y(t0) в конечное Y(Т) є Q1, оставаясь в области допустимых состояний Y(t) є Q(Y) при всех t є [t0, t]. Условие (2) называют критерием оптимальности.
Критерий оптимальности в нашем случае - состав выходных целевых потоков (кубовой жидкости Xw и дистиллята Xd), заданный технологическим регламентом.
Для контроля двух составов необходимо использовать комплексный показатель. Его определяют обычно с помощью функции желательности [7].
Рассмотрим построение функций желательности для ограничений:

Функция желательности d1 относится к ограничению (3), d1=1 (желательная функция), если ограничение (3) выполняется, и d1=0, если ограничение (3) не выполняется. С точностью до 0.01 функция желательности d1 определяется по следующей логической схеме:
Если Xd <0.94, то d1=0;
если Xd >0.96, то d1=1;
если Xd >0.94 и Xd <0.96, то d1=( Xd -0.94)/0.02.
Аналогично d1 вводим функцию желательности d2, контролирующую выполнение ограничения (4). Величина d2 определяется по следующей логической схеме:
Если Xw <0.04, то d2=1;
если Xw >0.06, то d2=0;
если Xw >0.04 и Xw <0.06, то d2=(0.06- Xw)/0.02.
Графически функции желательности d1 и d2 представлены на рис. 2.
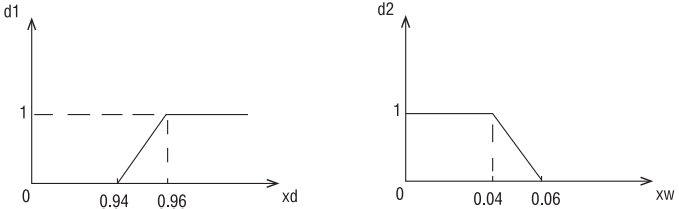
Рис. 2. Функции желательности, контролирующие выполнение ограничений.
Комплексный показатель, контролирующий выполнение обоих ограничений (3) и (4), может быть представлен как геометрическое среднее частных функций желательности:
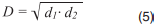
Если удается добиться того, чтобы D=1, то выполняются оба ограничения по составу выходных потоков процесса ректификации. Оптимизационная задача управления процессом состоит в определении значений расхода флегмы и производительности кипятильника, при которых D=Dmax.
Для решения поставленной задачи используется математическая модель процесса ректификации в колонне тарельчатого типа, которая состоит из системы уравнений, определяющей распределение концентрации в потоках пара и жидкости по высоте колонны [5]. Для построения модели вся колонна высотой H разбивается на бесконечно малые элементы величиной dh, и для каждого такого элемента записываются: основное уравнение массопередачи [4] (для жидкой и паровой фаз, для укрепляющей и исчерпывающей частей колонны), рассчитываются мольные доли легколетучего компонента в жидкой и паровой фазах на каждом элементарно малом участке насадки. В результате итерационного метода решения данной системы уравнений находим реальные значения концентраций кубовой жидкости и дистиллята при определенных условиях работы колонны. И в математическом обеспечении системы управления закладывается эта модель с применением метода сканирования к определению оптимального режима работы колонны.
Разработанная математическая модель, может быть использована для управления процессом ректификации по возмущению. Для измеренных значений расхода питающего потока и его состава (возмущающие воздействия) рассчитываются оптимальные значения расхода флегмы и температуры термостата (управляющие воздействия), при которых обеспечиваются заданные составы кубовой жидкости и дистиллята. Найденное значение расхода флегмы выдается в качестве задания насосу подачи флегмы, а найденная температура посылает задание на термостат.
Таким образом, предложенный алгоритм оптимального управления процессом ректификации в колонне тарельчатого типа позволит своевременно обнаруживать нестандартные ситуации при работе системы и принимать необходимые меры по их нейтрализации, что в конечном итоге позволит улучшить качество продукта, увеличить производительность установки, сэкономить энергоресурсы.
Список литературы
1. Анисимов И.В. Автоматическое регулирование процесса ректификации. – Изд. 2-е. – М. : Гостоптехиздат, 1961. – 178 с.
2. Песков Н.П. Система оптимального управления ректификацией этаноламинов с использованием математической модели процесса // Современные проблемы науки и образования. – 2011. – № 6
3. Дудников Е.Г. Автоматическое управление в химической промышленности. – М. : Химия, 1987. – 312 с.
4. Кафаров В.В. Основы массопередачи. – М. : Химия, 1975. – 285 с.
5. Кафаров В.В., Глебов М.Б. Математическое моделирование основных процессов химических производств : учеб. пособие. – М. : Высш. шк., 1991. – 277 с.
6. Мончарж Э.М. Постановка задач автоматизации технологических процессов. –Н. Новгород, 2003. – 87 с.
7. Холоднов В.А., Дьяконов В.П. Математическое моделирование и оптимизация химико-технологических процессов : практ. руководство. – СПб.: Профессионал, 2003. – 312 с.
8. Чураков Е.П. Оптимальные и адаптивные системы : учеб. пособие для вузов. – М. : Энергоатомиздат, 1987. – 256 с.
9. Ермоленко, А.Д. Автоматизация процессов нефтепереработки: уч. пос./ СПб.: Профессия, 2012. - 304 c.






